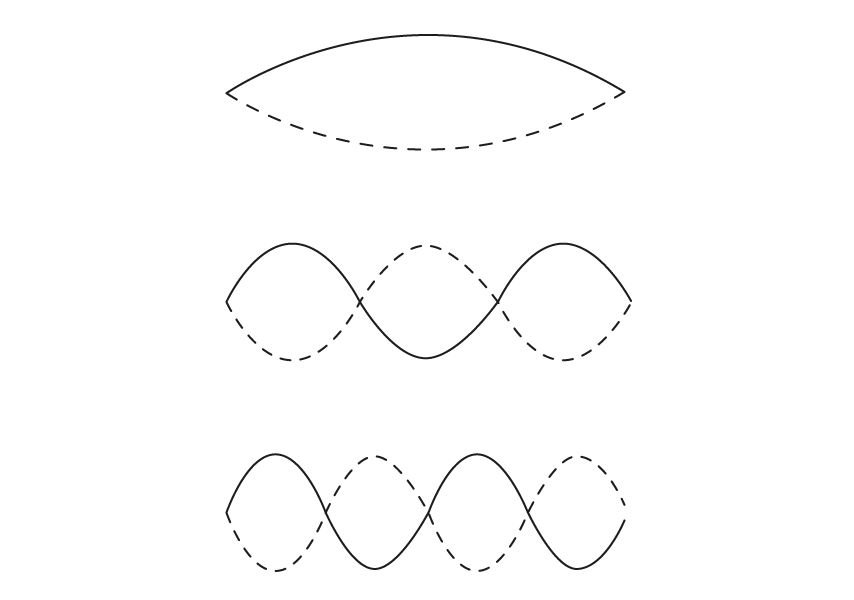
State three conditions which are required for the formation of a standing wave.
Outline one difference between standing waves and travelling waves.
A standing wave is made up of nodes and antinodes.
State what is meant by
(i) a node
[1]
(ii) an antinode.
[1]
The length L shows 2.5 full wavelengths of a standing wave in a column of air.

(i) Identify the points marked X and Y.
[2]
(ii) State the boundary conditions for the formation of this standing wave.
[2]
Did this page help you?