Hooke's Law (DP IB Physics) : Revision Note
Hooke's Law
When a force is applied to each end of a spring, it stretches
This phenomenon occurs for any material with elasticity, such as a wire or a bungee rope
A material obeys Hooke’s Law if:
The extension of the material is directly proportional to the applied force (load) up to the limit of proportionality
This linear relationship is represented by the Hooke’s law equation:
Where:
FH = elastic restoring force (N)
k = spring constant (N m–1)
x = extension (m)
The spring constant, k is a property of the material being stretched and measures the stiffness of a material
The larger the spring constant, the stiffer the material
Hooke's Law applies to both extensions and compressions:
The extension of an object is determined by how much it has increased in length
The compression of an object is determined by how much it has decreased in length
The extension x is the difference between the unstretched and stretched length
extension = stretched length − unstretched length
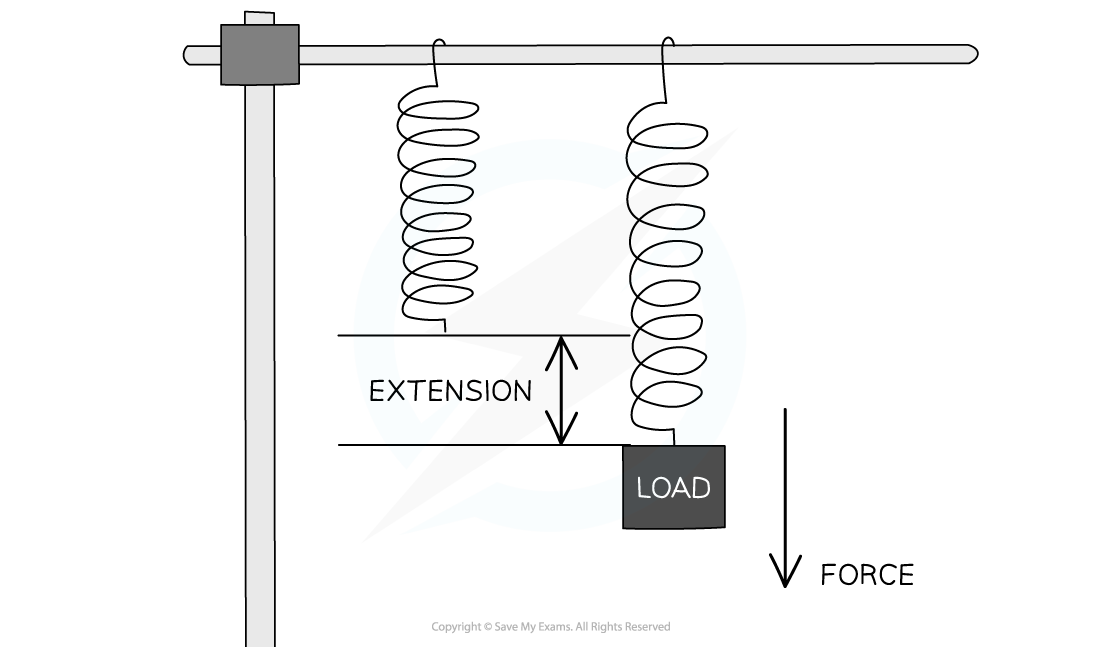
Stretching a spring with a load produces a force that leads to an extension
Force–Extension Graphs
The way a material responds to a given force can be shown on a force-extension graph
Every material will have a unique force-extension graph depending on how brittle or ductile it is
A material may obey Hooke's Law up to a point
This is shown on its force-extension graph by a straight line through the origin
As more force is added, the graph starts to curve slightly as Hooke's law no longer applies
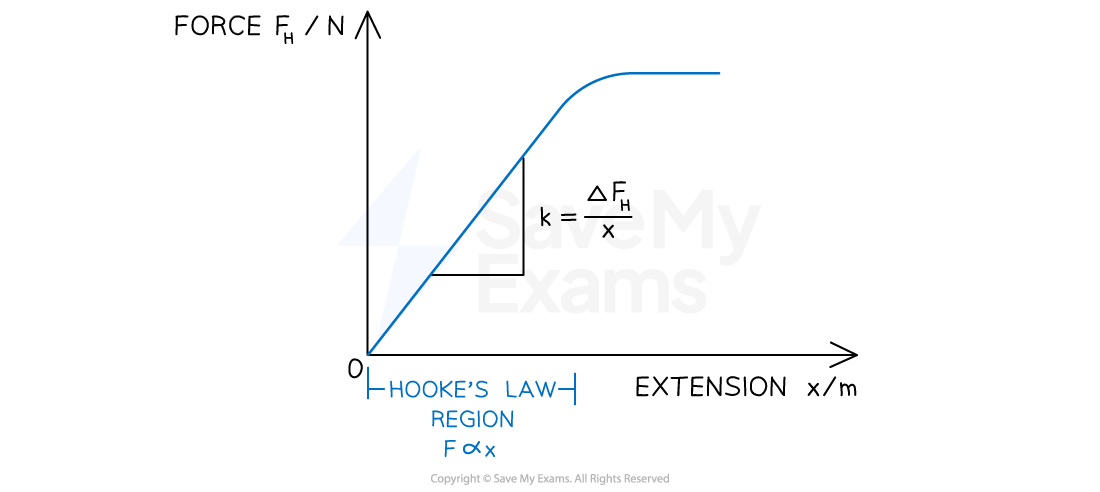
The Hooke's Law region of a force-extension graph is a straight line. The spring constant is the gradient of that region
The gradient of the linear portion of this graph is equal to the spring constant k
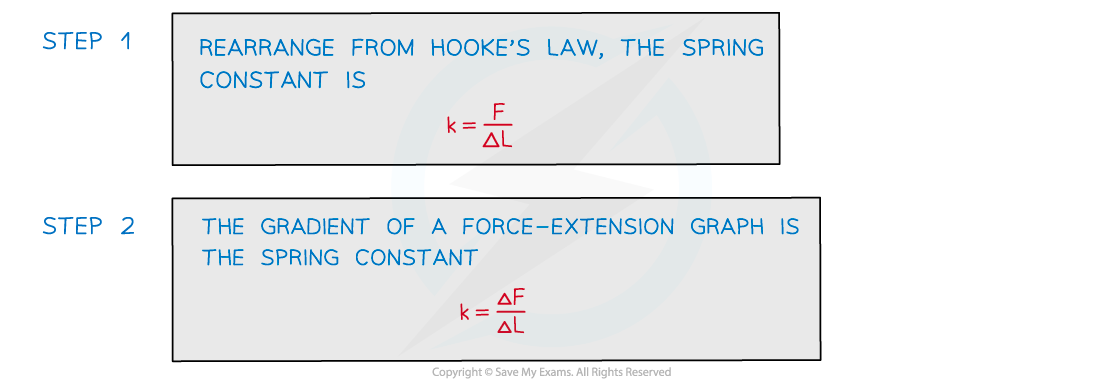
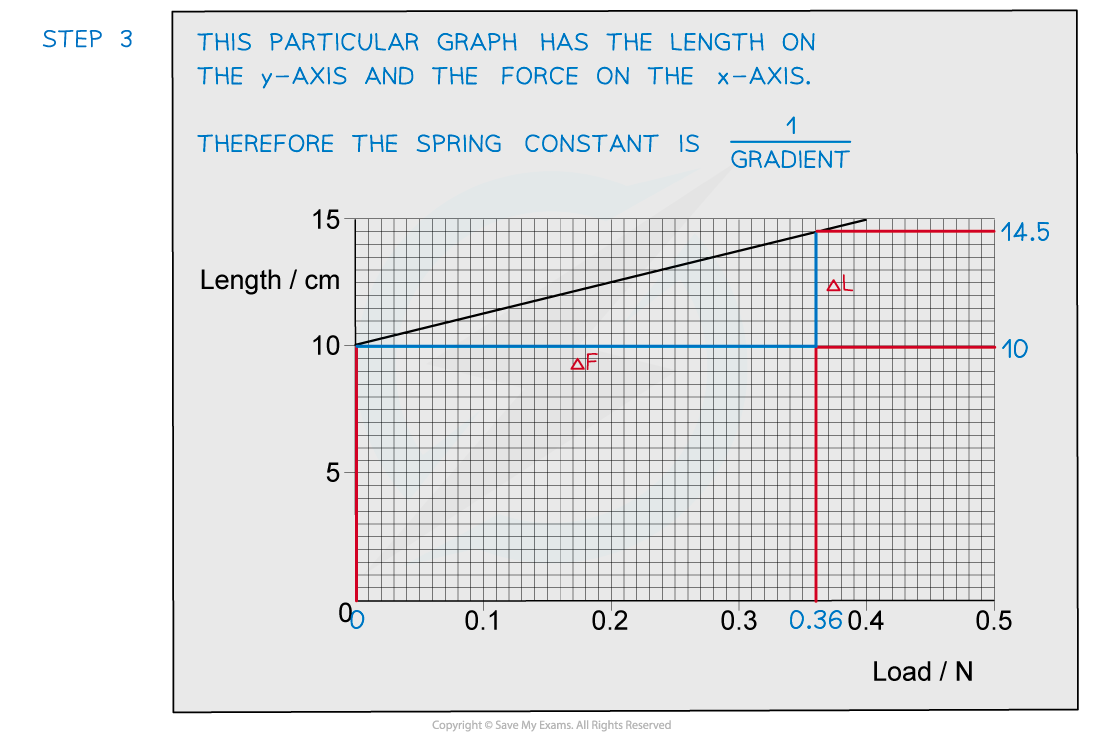
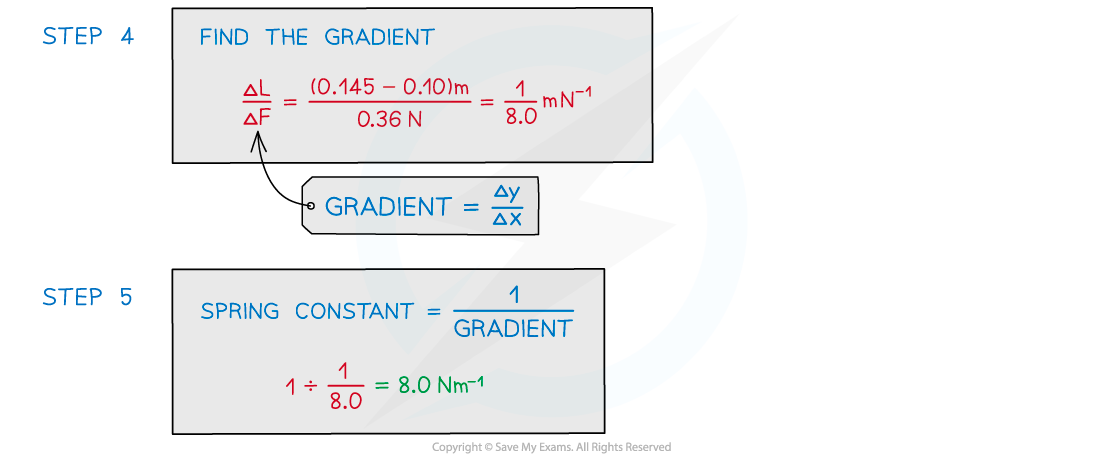
Worked Example
A spring was stretched with increasing load.
The graph of the results is shown below.

Determine the spring constant.
Answer:
Examiner Tips and Tricks
Always double check the axes before finding the spring constant as the gradient of a force-extension graph.
Exam questions often swap the force (or load) onto the x-axis and extension (or length) on the y-axis. In this case, the gradient is not the spring constant, it is instead.
Make sure that you put the extension of the object into the equation for x and not just the length.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
