Conservation of Linear Momentum (DP IB Physics) : Revision Note
Conservation of Linear Momentum
Linear Momentum
When an object with mass is in motion and therefore has a velocity, the object also has momentum
Linear momentum is the momentum of an object that is moving in only one dimension
The linear momentum of an object remains constant unless an external resultant force acts upon the system
Momentum is defined as the product of mass and velocity
Where:
= momentum, measured in kg m s−1
= mass, measured in kg
= velocity, measured in m s−1
Direction of Momentum
Momentum is a vector quantity with both magnitude and direction
The initial direction of motion is usually assigned the positive direction
If a ball of mass 60 g travels at 2 m s−1, it will have a momentum of 0.12 kg m s−1
If it then hits a wall and rebounds in the exact opposite direction at the same speed, it will have a momentum of −0.12 kg m s−1
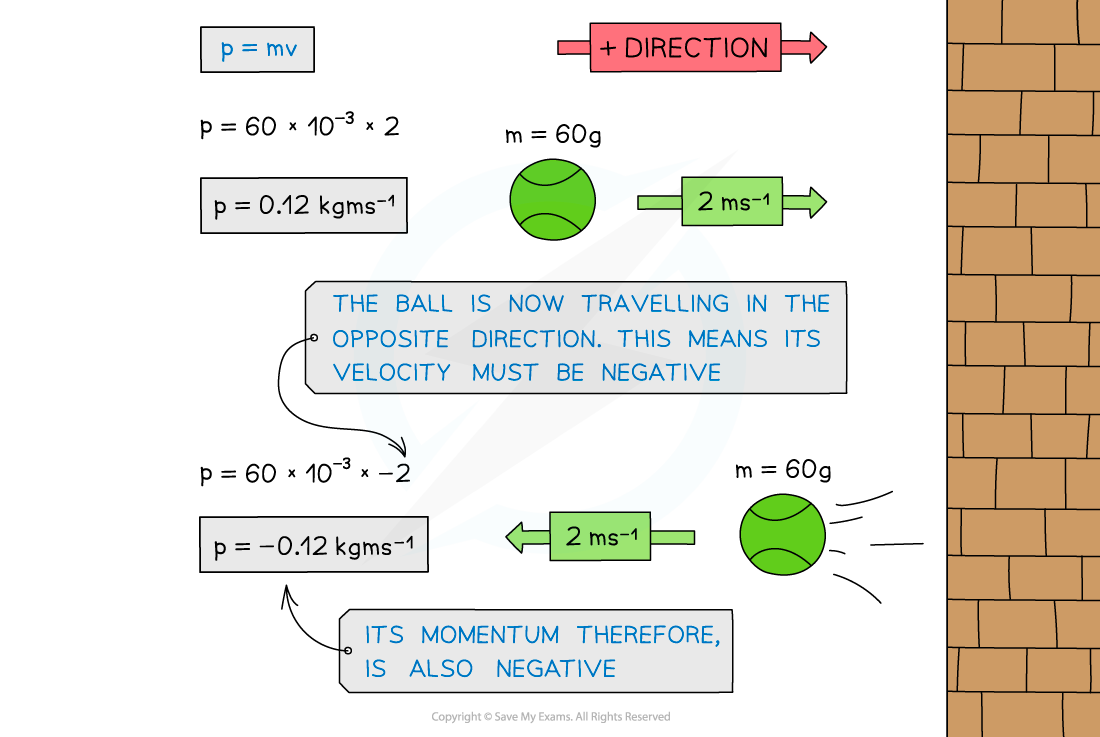
When the ball is travelling in the opposite direction, its velocity is negative. Since momentum = mass × velocity, its momentum is also negative
Conservation of Linear Momentum
The principle of conservation of linear momentum states that:
The total linear momentum before a collision is equal to the total linear momentum after a collision unless the system is acted on by a resultant external force
Therefore:
momentum before = momentum after
Momentum is a vector quantity, therefore:
opposing vectors can cancel each other out, resulting in a net momentum of zero
an object that collides with another object and rebounds, has a positive velocity before the collision and a negative velocity after
Momentum, just like energy, is always conserved
For example:
Ball A moves with an initial velocity of
Ball A collides with Ball B which is stationary
After the collision, both balls travel in opposite directions
Taking the direction of the initial motion of Ball A as the positive direction (to the right)
The momentum before the collision is
The momentum after the collision is
The minus sign shows that Ball A travels in the opposite direction to the initial travel
If an object is stationary, like Ball B before the collision, then it has a momentum of zero
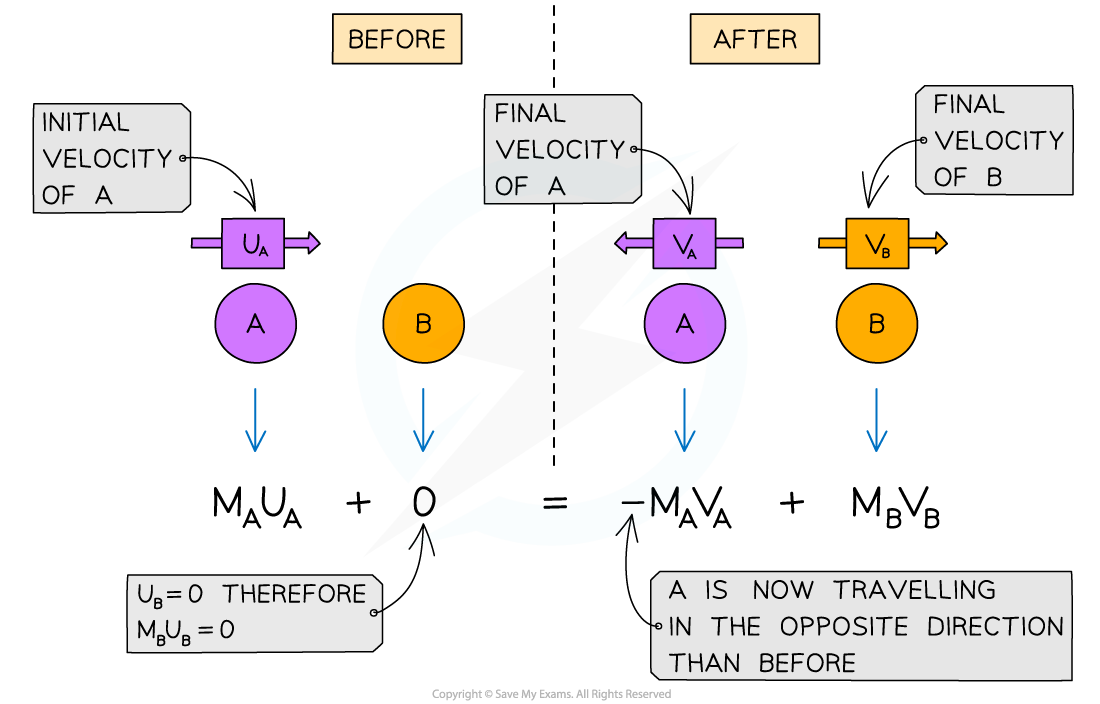
The conservation of momentum for two objects A and B colliding then moving apart
Worked Example
A tennis ball of mass 60 g travels to the right with a speed of 75 m s−1.
A brick of mass 3 kg is thrown to the right at a speed of 1.5 m s−1.
Determine which object has the greatest momentum.
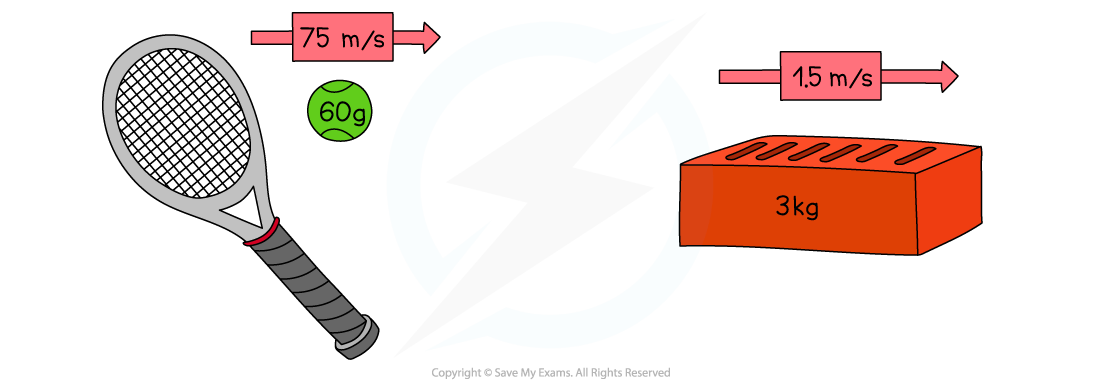
Answer:

Both the tennis ball and the brick have the same momentum
Even though the brick is much heavier than the ball, the ball is travelling much faster than the brick
This means that on impact, they would both exert a similar force (depending on the time it takes for each to come to rest)
Worked Example
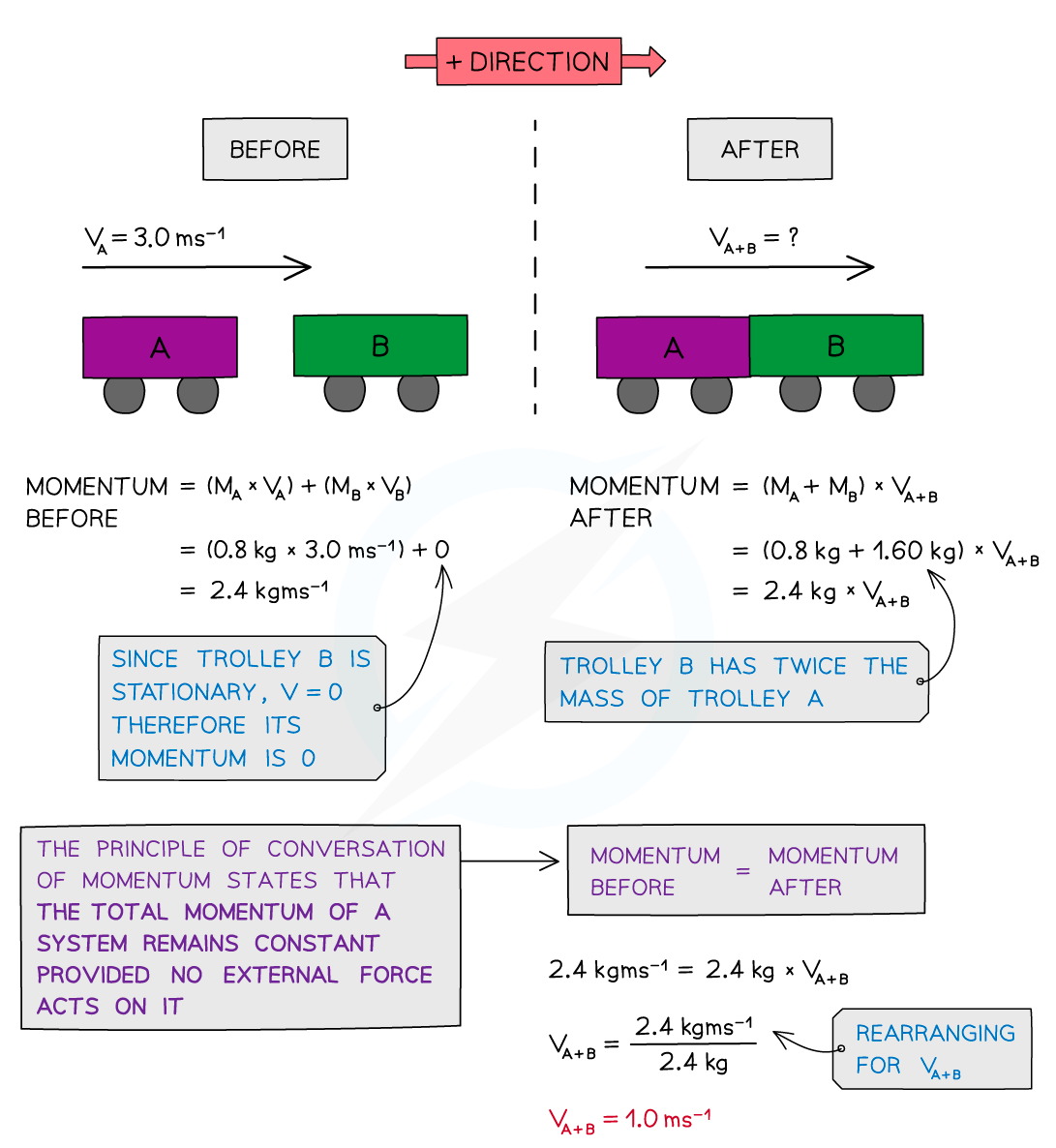
Trolley A of mass 0.80 kg collides head-on with stationary trolley B whilst travelling at 3.0 m s–1.
Trolley B has twice the mass of trolley A. On impact, the trolleys stick together.
Using the conservation of momentum, calculate the common velocity of both trolleys after the collision.
Answer:
Worked Example
The diagram shows a car and a van which is initially at rest, just before and just after the car collides with the van.
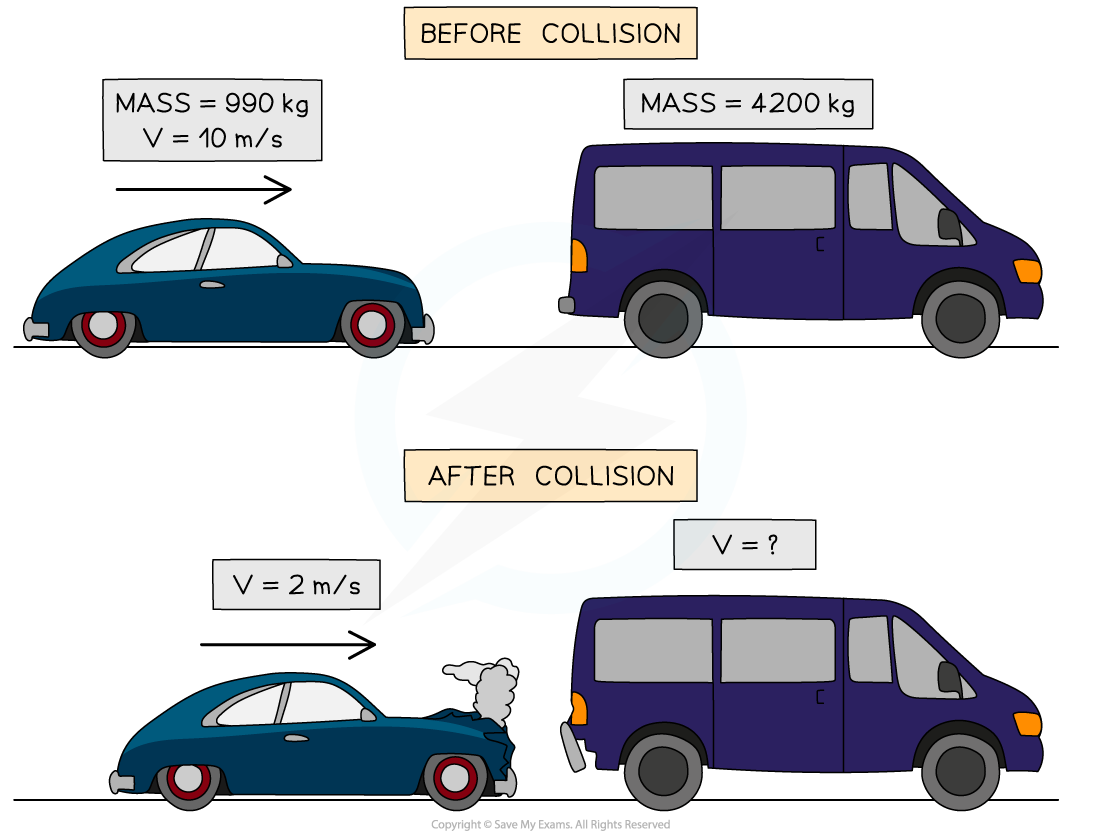
Use the idea of conservation of momentum to calculate the velocity of the van when it is pushed forward by the collision.
Answer:
Step 1: State the principle of the conservation of momentum
In a closed system, the total momentum before an event is equal to the total momentum after the event
Step 2: Calculate the total momentum before the collision
p = mv
Momentum of car:
pcar = 990 × 10 = 9900 kg m/s
Momentum of van:
The van is at rest, therefore v = 0 m/s and pvan = 0 kg m/s
Total momentum before:
pbefore = 9900 + 0 = 9900 kg m/s
Step 3: Calculate the momentum after the collision
Conservation of momentum states that total momentum after collision = 9900 kg m/s
Momentum of car:
pcar = 990 × 2 = 1980 kg m/s
Momentum of van:
pvan = 4200 × v = 4200v kg m/s
Step 4: Calculate the velocity of the van after the collision
Total momentum after collision:
pcar + pvan = 1980 + 4200v = 9900
Rearrange to make v the subject:
4200v = 9900 − 1980
m/s
The velocity of the van when it is pushed forward by the collision v = 1.89 m/s
Examiner Tips and Tricks
If it is not given in the question already, drawing a diagram of before and after helps keep track of all the masses and velocities (and directions) in the conservation of momentum questions. Even if one is given, label all the values that you have been given in the question to make sure you're substituting in the correct masses and velocities.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
