IBPhysicsDPSLRevision NotesNuclear & Quantum PhysicsRadioactive DecayMass Defect & Nuclear Binding Energy

Mass Defect & Nuclear Binding Energy (DP IB Physics): Revision Note

Katie M

Author

Katie M

Last updated

DP Physics: SLDP Physics: HL

Mass Defect & Nuclear Binding Energy

  • Experiments into nuclear structure have found that the total mass of a nucleus is less than the sum of the masses of its constituent nucleons

    • In other words, the combined mass of 6 separate protons and 6 separate neutrons is more than the mass of a carbon-12 nucleus 

    • This difference in mass is known as the mass defect 

  • Mass defect is defined as:

The difference between the measured mass of a nucleus and the sum total of the masses of its constituents

  • The mass defect Δm of a nucleus can be calculated using:

increment m space equals space Z m subscript p space plus space left parenthesis A space – space Z right parenthesis m subscript n space – space m subscript t o t a l end subscript

  • Where:

    • Z = proton number

    • A = nucleon number

    • mp = mass of a proton (kg)

    • mn = mass of a neutron (kg)

    • mtotal = measured mass of the nucleus (kg)

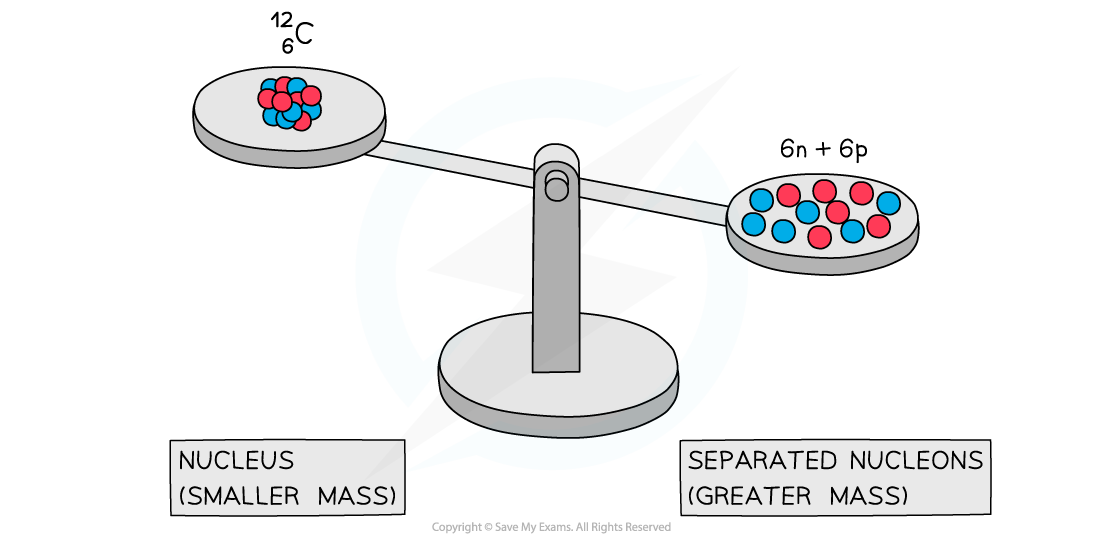
Binding Energy, downloadable AS & A Level Physics revision notes

A system of separated nucleons has a greater mass than a system of bound nucleons

  • Due to mass-energy equivalence, a decrease in mass implies that energy must be released

  • Energy and mass are proportional, so the total energy of a nucleus is less than the sum of the energies of its constituent nucleons

  • Binding energy is defined as:

The energy required to break a nucleus into its constituent protons and neutrons

  • The formation of a nucleus from a system of isolated protons and neutrons releases energy

Worked Example

The binding energy per nucleon is 7.98 MeV for an atom of Oxygen-16 (16O).

Determine an approximate value for the energy required, in MeV, to completely separate the nucleons of this atom.

Answer:

Step 1: List the known quantities

  • Binding energy per nucleon, E = 7.98 MeV

Step 2: State the number of nucleons

  • The number of nucleons is 8 protons and 8 neutrons, therefore 16 nucleons in total

Step 3: Find the total binding energy

  • The binding energy for oxygen-16 is:

7.98 × 16 = 127.7 MeV

Step 4: State the final answer

  • The approximate total energy needed to completely separate this nucleus is 127.7 MeV

Examiner Tips and Tricks

The terms binding energy and mass defect can cause students confusion, so be careful when using them in your explanations.

Avoid describing the binding energy as the energy stored in the nucleus – this is not correct – it is energy that must be put into the nucleus to separate all the nucleons.

The same goes for the term mass defect, make sure to only use this when all the nucleons are separated and not to describe the decrease in mass which occurs during radioactive decay.

Mass-Energy Equivalence

  • Einstein showed in his Theory of Relativity that matter can be considered a form of energy, and hence, he proposed:

    • mass can be converted into energy

    • energy can be converted into mass

  • This is known as mass-energy equivalence, and can be summarised by the equation:

increment E space equals space increment m c squared

  • Where:

    • E = energy (J)

    • m = mass (kg) 

    • c = the speed of light  (m s-1)

  • Some examples of mass-energy equivalence are:

    • The fusion of hydrogen into helium in the centre of the sun

    • The fission of uranium in nuclear power plants

    • Nuclear weapons

    • High-energy particle collisions in particle accelerators

Atomic Mass Unit

  • The atomic mass unit is commonly used in nuclear physics to express the mass of subatomic particles

  • It is defined as: 

Exactly one twelfth open parentheses 1 over 12 close parentheses the mass of a neutral atom of carbon-12

  • Atomic mass unit u is roughly equal to the mass of one proton or neutron:

    • 1 u = 1.661 × 10−27 kg

  • Using more precise values for well-known constants, a useful conversion factor can be determined

  • A particle with a mass of 1 u has an equivalent energy of 

E space equals space m c squared space equals space open parentheses 1.66053907 cross times 10 to the power of negative 27 end exponent close parentheses cross times open parentheses 2.99792458 cross times 10 to the power of 8 close parentheses squared space equals space 1.49241809 cross times 10 to the power of negative 10 end exponent space straight J

  • Converting to eV by using the precise value of the elementary charge gives

E space equals space fraction numerator 1.49241809 cross times 10 to the power of negative 10 end exponent over denominator 1.60217663 cross times 10 to the power of negative 19 end exponent end fraction space equals space 931.494 space MeV

  • Therefore, the unified atomic mass unit can be used to quickly convert between nuclear mass and energy using:

    • 1 u = 1.661 × 10−27 kg = 931.5 MeV c−2

Worked Example

Calculate the binding energy per nucleon, in MeV, for the radioactive isotope potassium-40 open parentheses straight K presubscript 19 presuperscript 40 close parentheses.

You may use the following data:

  • Nuclear mass of potassium-40 = 39.953 548 u

  • Mass of one neutron = 1.008 665 u

  • Mass of one proton = 1.007 276 u

Answer:

Step 1: Identify the number of protons and neutrons in potassium-40

  • Proton number, Z = 19

  • Neutron number, N = 40 – 19 = 21

Step 2: Calculate the mass defect, Δm

  • Proton mass, mp = 1.007 276 u

  • Neutron mass, mn = 1.008 665 u

  • Mass of potassium-40, mtotal = 39.953 548 u

Δm = Zmp + Nmn – mtotal

Δm = (19 × 1.007276) + (21 × 1.008665) – 39.953 548

Δm = 0.36666 u

Step 3: Convert mass units from u to kg

  • 1 u = 1.661 × 10–27 kg

Δm = 0.36666 × (1.661 × 10–27) = 6.090 × 10–28 kg

Step 4: Write down the equation for mass-energy equivalence

E = Δmc2

  • Where c = 3.0 × 108 m s–1

Step 5: Calculate the binding energy, E

E = 6.090 × 10–28 × (3.0 × 108)2 = 5.5 × 10–11 J

Step 6: Determine the binding energy per nucleon and convert J to MeV

  • Take the binding energy and divide it by the number of nucleons

  • 1 MeV = 1.6 × 10–13 J

Binding energy per nucleon = fraction numerator 5.5 cross times 10 to the power of negative 11 end exponent over denominator 40 end fraction space equals space 1.375 cross times 10 to the power of negative 12 end exponent J

Binding energy per nucleon = fraction numerator 1.375 cross times 10 to the power of negative 12 end exponent over denominator 1.6 cross times 10 to the power of negative 13 end exponent end fraction = 8.594 MeV

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Applications of RadioactivityNext:Binding Energy per Nucleon Curve
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.