State the distinctive features of a single-slit interference pattern using monochromatic light.
The monochromatic light is replaced by a source of white light.
The paragraph below describes how this change would affect the interference pattern. Choose appropriate words to fill the gaps.
The central maximum would be __________, and each subsidiary maximum would be composed of a ___________.
The ___________ wavelength would appear nearest to the central maximum, and the _____________ wavelength would appear furthest from the central maximum.
The fringe spacings would be ___________ and the maxima would be ____________.
The white light source is replaced, first with red laser light and then blue laser light.
Explain the difference in the diffraction patterns between the red and blue light.
The diagram below shows the intensity patterns for blue light.
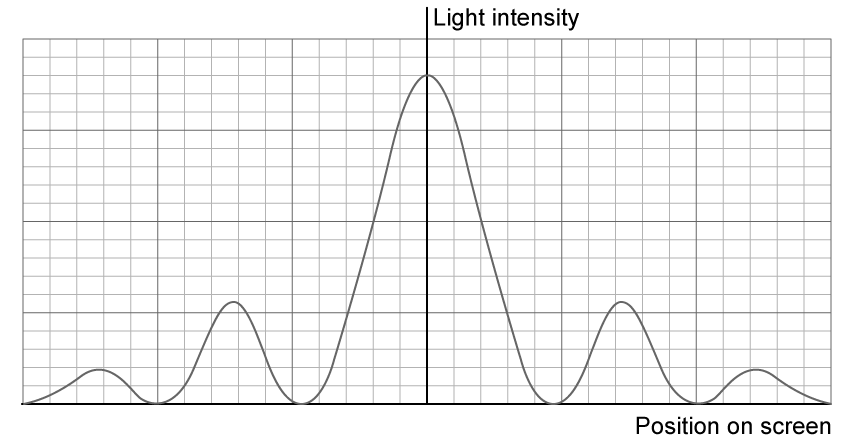
On the same axes, sketch the intensity pattern for red light.
Did this page help you?

























































