Describe the conditions required for an object to perform simple harmonic motion (SHM).
A student is investigating the simple harmonic motion of a mass oscillating at the end of a spring.
The graph shows the variation with time of the displacement
of the spring.
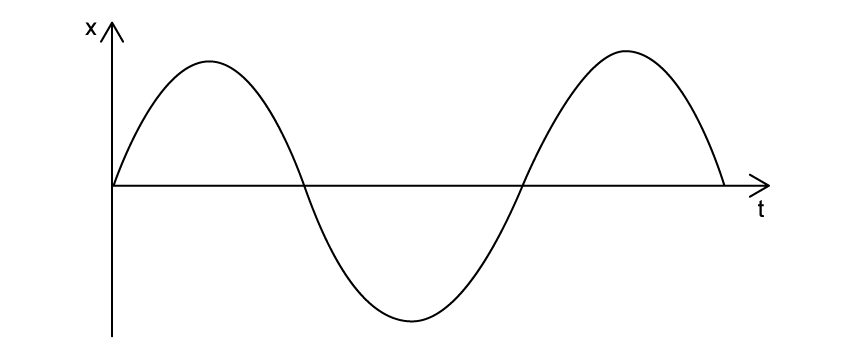
On the graph, label:
(i) the time period
[1]
(ii) the amplitude .
[1]
Was this exam question helpful?