Single-Slit Diffraction (DP IB Physics) : Revision Note

Single Slit Intensity Pattern

Single Slit Diffraction Pattern

• The diffraction pattern of monochromatic light passing through a single rectangular slit, is a series of light and dark fringes on a faraway screen

•  This is similar to a double slit diffraction pattern: 

  • The bright fringes are also areas of maximum intensity, produced by the constructive interference of each part of the wavefront as it passes through the slit

  • The dark fringes are also areas of zero or minimum intensity, produced by the destructive interference of each part of the wavefront as it passes through the slit

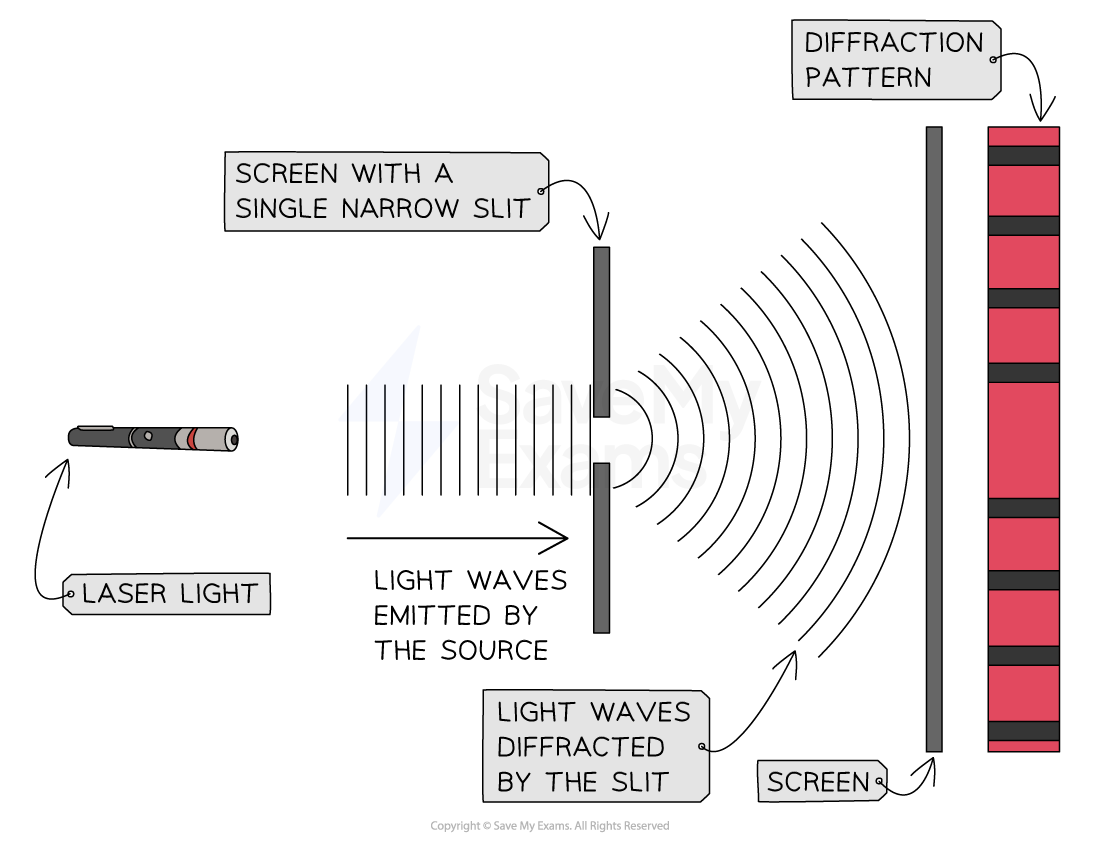
The diffraction pattern produced by a laser beam diffracted through a single slit onto a screen is different to the diffraction pattern produced through a double slit

• However, the single and double-slit diffraction patterns are different

• The central maximum of the diffraction pattern is:

  • Much wider and brighter than the other bright fringes

  • Much wider than that of the double-slit diffraction pattern

• On either side of the wide central maxima for the single slit diffraction pattern are much narrower and less bright maxima

  • These get dimmer as the order increases

Single Slit Intensity Pattern

• If a laser emitting blue light is directed at a single slit, where the slit width is similar in size to the wavelength of the light, its intensity pattern will be as follows:

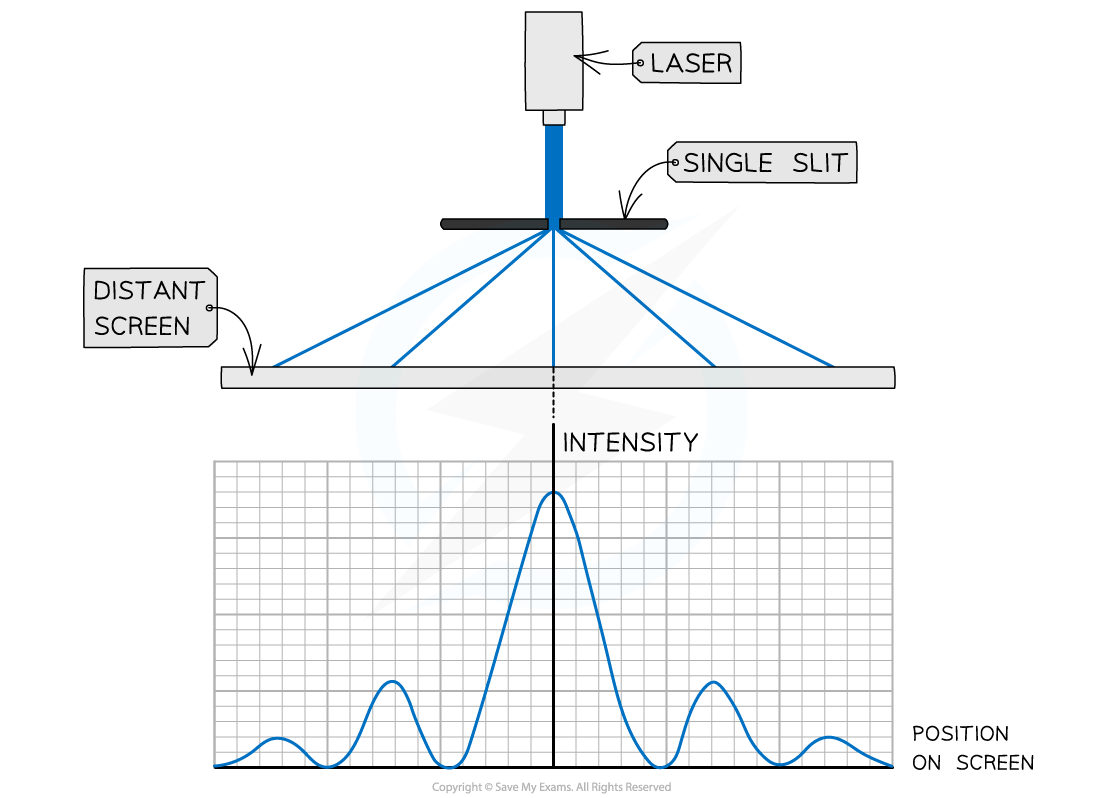
The intensity pattern of blue laser light diffracted through a single slit

• The features of the single slit intensity pattern are: 

  • The central bright fringe has the greatest intensity of any fringe and is called the central maximum

  • The dark fringes are regions with zero intensity

  • The intensity of each bright fringe gradually decreases on either side of the central maxima

Changes in Wavelength

• If the wavelength passing through the gap increases, the wave diffracts more

• This means the angle of diffraction of the waves increases as they pass through the slit

  • As a result, the width of the bright maxima also increases

• Red light

  • has the longest wavelength on the visible light spectrum

  • produces a diffraction pattern with wider fringes (due to a larger angle of diffraction)

• Blue light

  • has a shorter wavelength on the visible light spectrum

  • produces a diffraction pattern with narrower fringes (due to a smaller angle of diffraction)

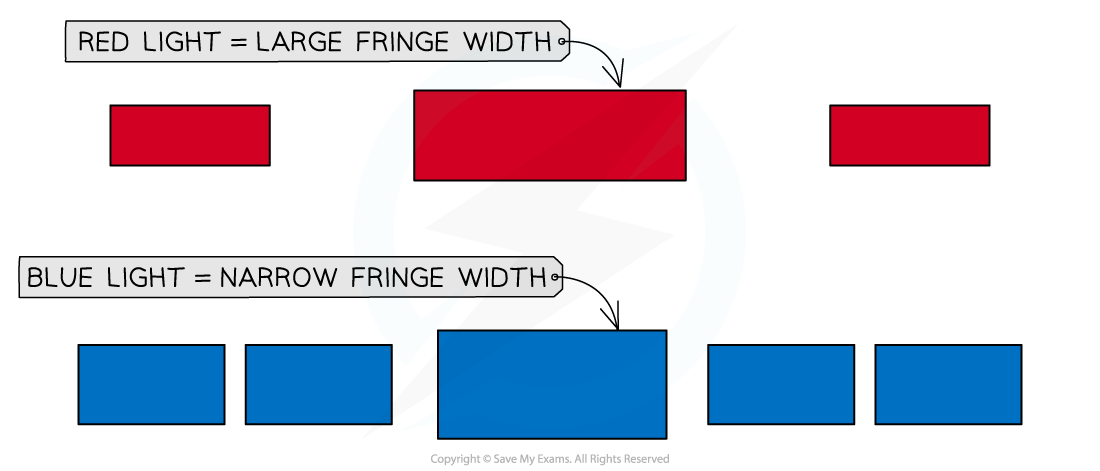
Fringe width depends on the wavelength of the light 

• If the blue laser is replaced with a red laser:

  • The light diffract more as the waves pass through the single slit

  • The fringes in the intensity pattern appear wider

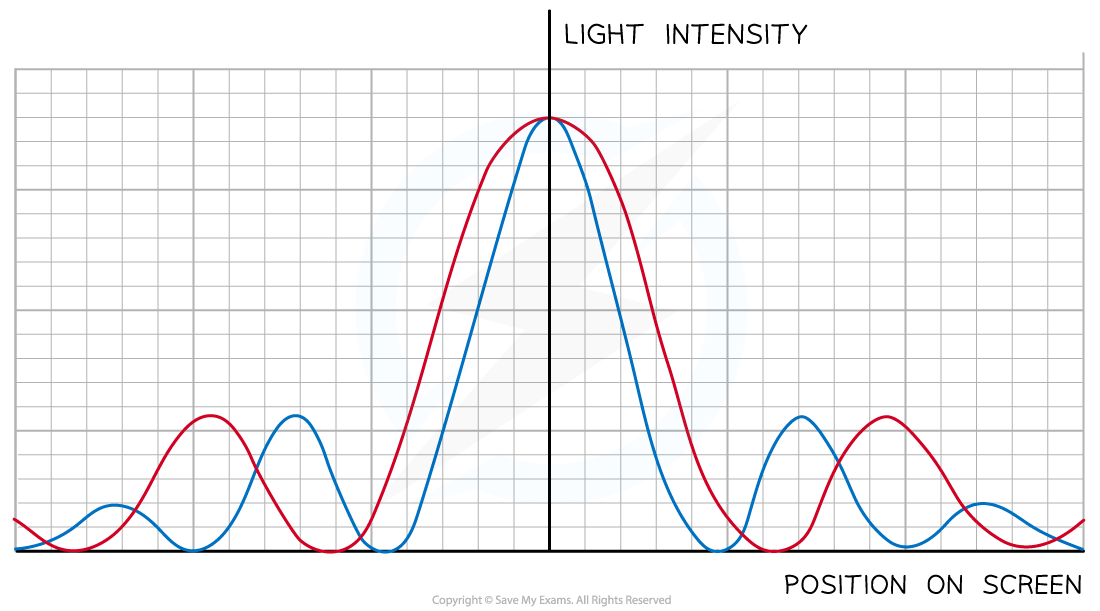
The intensity pattern of red laser light shows that longer wavelengths diffract more than shorter wavelengths

Changes in Slit Width

• If the slit is made narrower:

  • the angle of diffraction is greater

  • the waves spread out more beyond the slit

• For a narrower slit, the intensity graph shows that: 

  • the intensity of the maxima decreases

  • the width of the central maxima increases

  • the spacing between fringes is wider

Single Slit Equation

• These properties of wavelength and slit width for single slit diffraction for the first minima can be explained using the equation:

• Where:

  • = the angle of diffraction of the first minima (°)

  • = wavelength of incident light (m)

  • = slit width (m)

• This equation tells us:

  • the longer the wavelength of light, the larger the angle of diffraction

  • the narrower the slit width then the larger the angle of diffraction

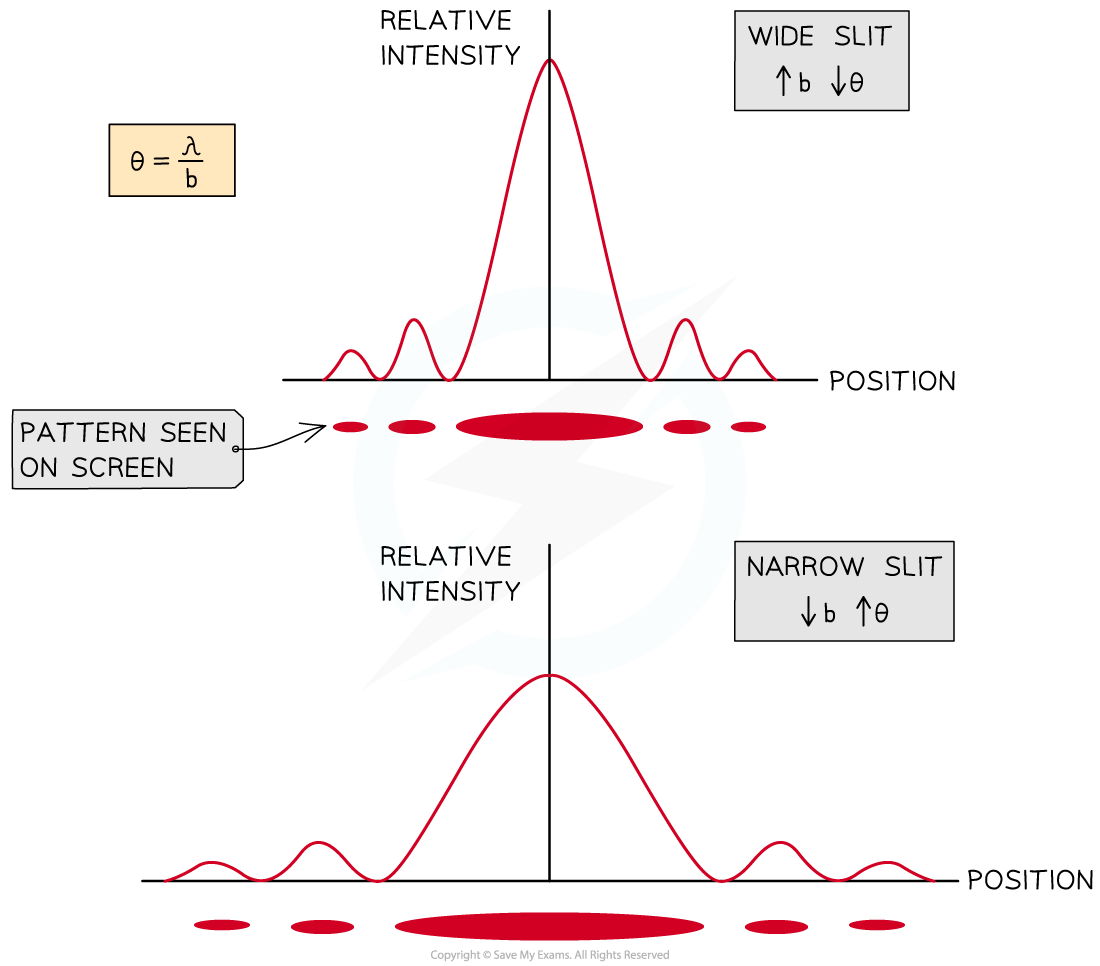
Slit width and angle of diffraction are inversely proportional. Increasing the slit width leads to a decrease in the angle of diffraction, hence the maxima appear narrower

Single Slit Geometry

• The diffraction pattern made by waves passing through a slit of width can be observed on a screen placed a large distance away

The geometry of single-slit diffraction

• If the distance between the slit and the screen is considerably larger than the slit width, :

  • The light rays can be considered as a set of plane wavefronts that are parallel to each other

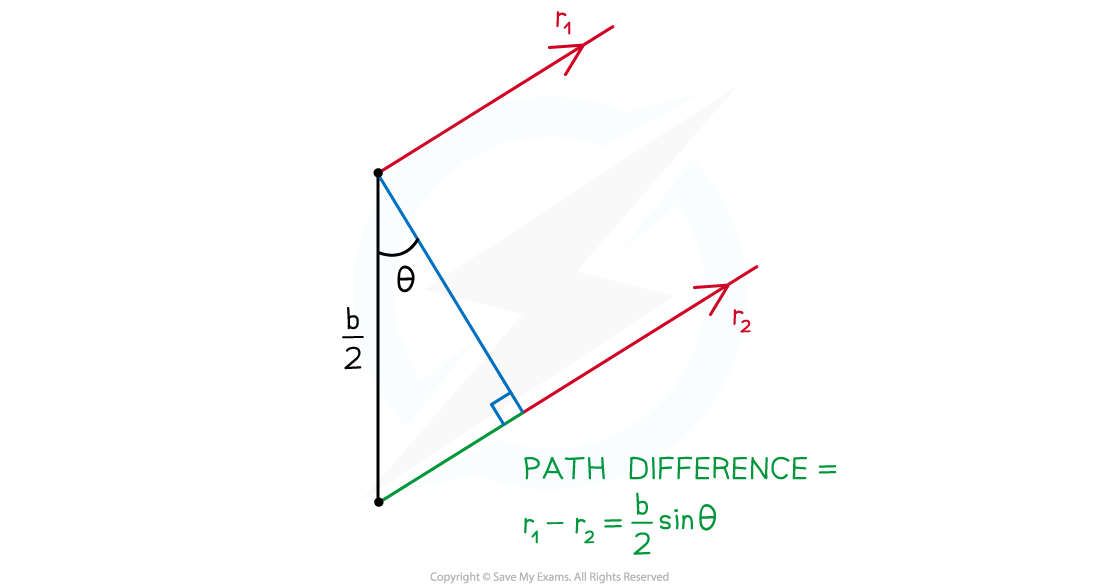
Determining the path difference using two parallel waves

• For two paths, and , travelling parallel to each other at an angle between the normal and the slit, the path difference will be:

path difference = 

• For a minima, or area of destructive interference:

The path difference must be a half-integral multiple of the wavelength

path difference = 

• Equating these two equations for path difference:

• Where n is a non-zero integer number, n = 1, 2, 3...

• Since the angle θ is small, the small-angle approximation may be used:

• Therefore, the first minima, n = 1, occurs at:

• This leads to the equation for the angle of diffraction of the first minima:

Double Slit Modulation

• When light passes through a double slit two types of interference occur:

  • The diffracted rays passing through one slit interfere with the rays passing through the other

  • Rays passing through the same slit interfere with each other

• This produces a double-slit intensity pattern where the single-slit intensity pattern modulates (adjusts) the intensity of the light on the screen

  • It looks like a double-slit interference pattern inscribed in the single-slit intensity pattern

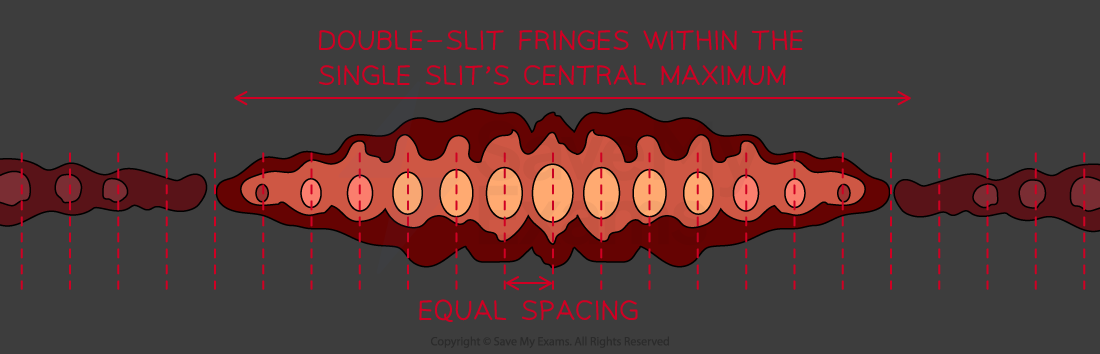
The double slit interference pattern is modulated inside the single slit intensity pattern

• The single-slit intensity pattern has a distinctive central maximum and subsequent maxima at lower intensity

• The double-slit interference pattern has equally spaced intensity peaks with maxima of equal intensity

• Together, the combined double slit intensity pattern has equally spaced bright fringes but now within a single slit 'envelope' 

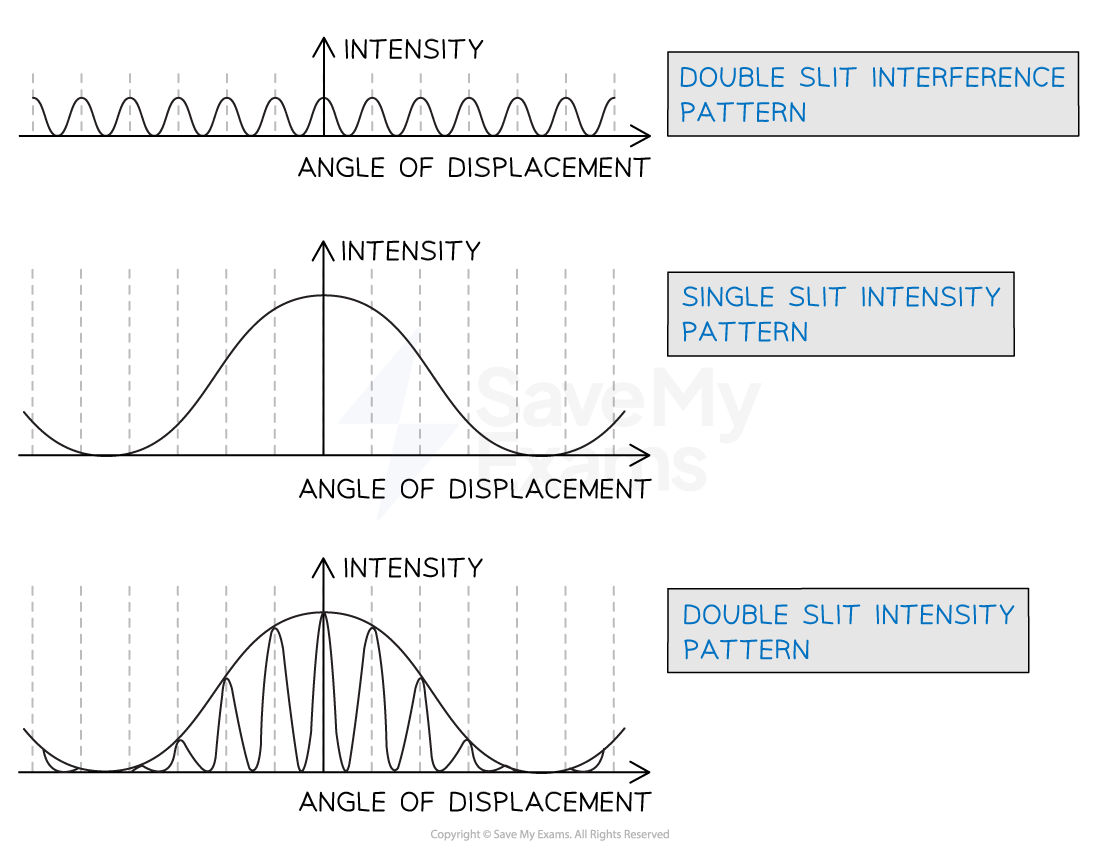
Combined single-slit intensity pattern and double-slit interference pattern

• This is assuming that:

  • The slit width is not negligible

  • The distance between the slits is much greater than their width