Interference of Waves (DP IB Physics) : Revision Note
Double Source Interference
Double-source interference involves producing a diffraction and an interference pattern using either:
The interference of two coherent wave sources
A single wave source passing through a double slit
Examples of double-source interference include:
A laser beam that creates bright and dark fringes on a screen
Two speakers emitting a coherent sound
Microwaves diffracted through two slits
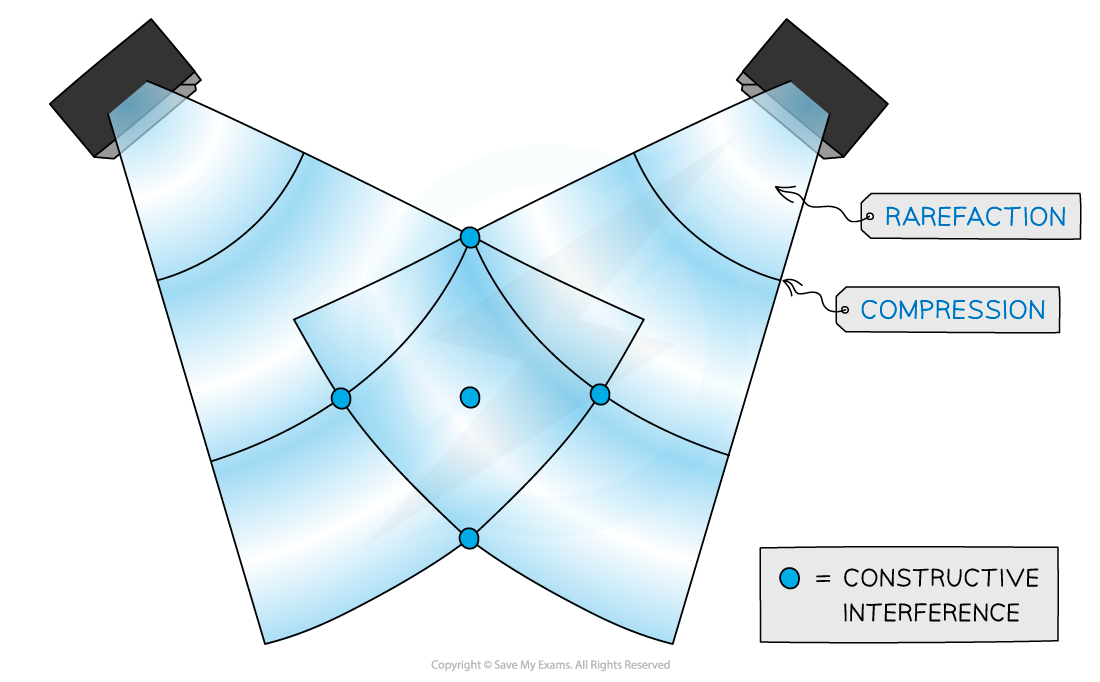
Sound wave interference from two speakers emitting a coherent sound
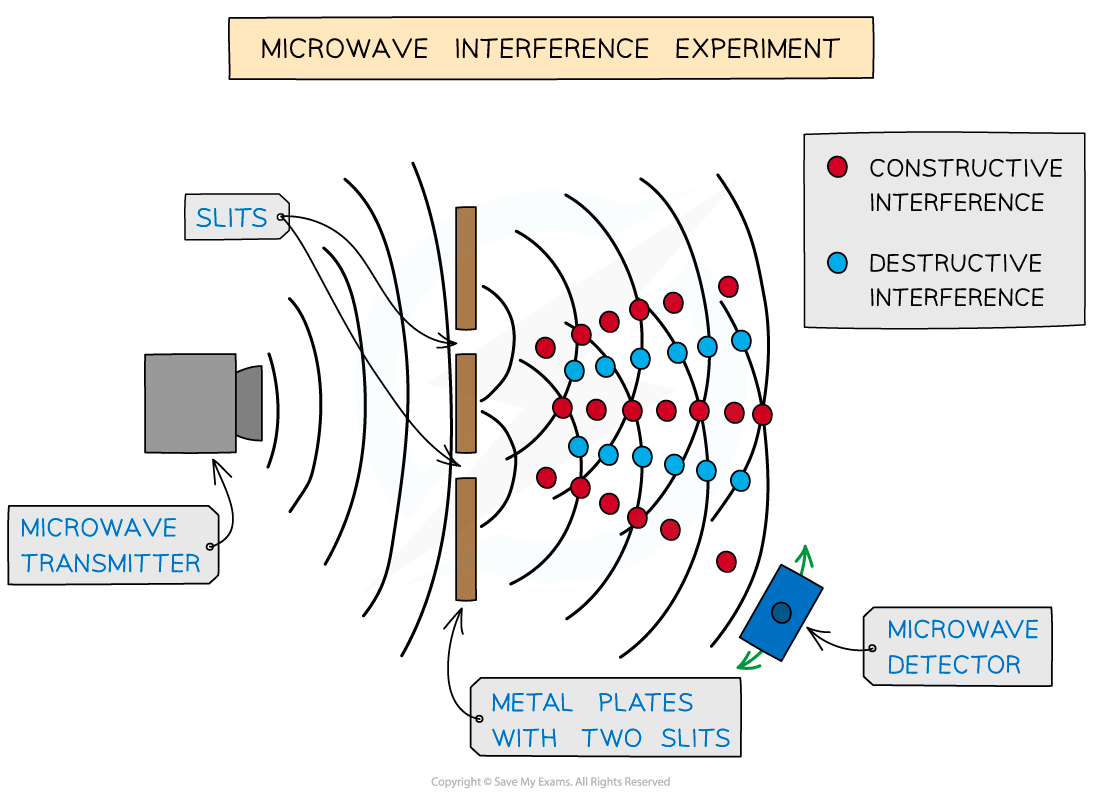
A microwave interference experiment creates a diffraction pattern with regions where microwaves are and are not detected
Interference
Interference is the effect observed due to the superposition of two or more waves
It can be seen clearly when waves overlap completely in phase or antiphase
The maximum amount of superposition occurs when two waves are in phase
They meet either peak-to-peak or trough-to-trough
This results in the two waves adding together
This is called constructive interference
The minimum amount of superposition occurs when two waves are in antiphase
They meet peak-to-trough
This results in the two waves cancelling each other out and having zero effect (there is an effect - that they cancel out)
This is called destructive interference
Constructive and destructive interference occurs when waves are coherent
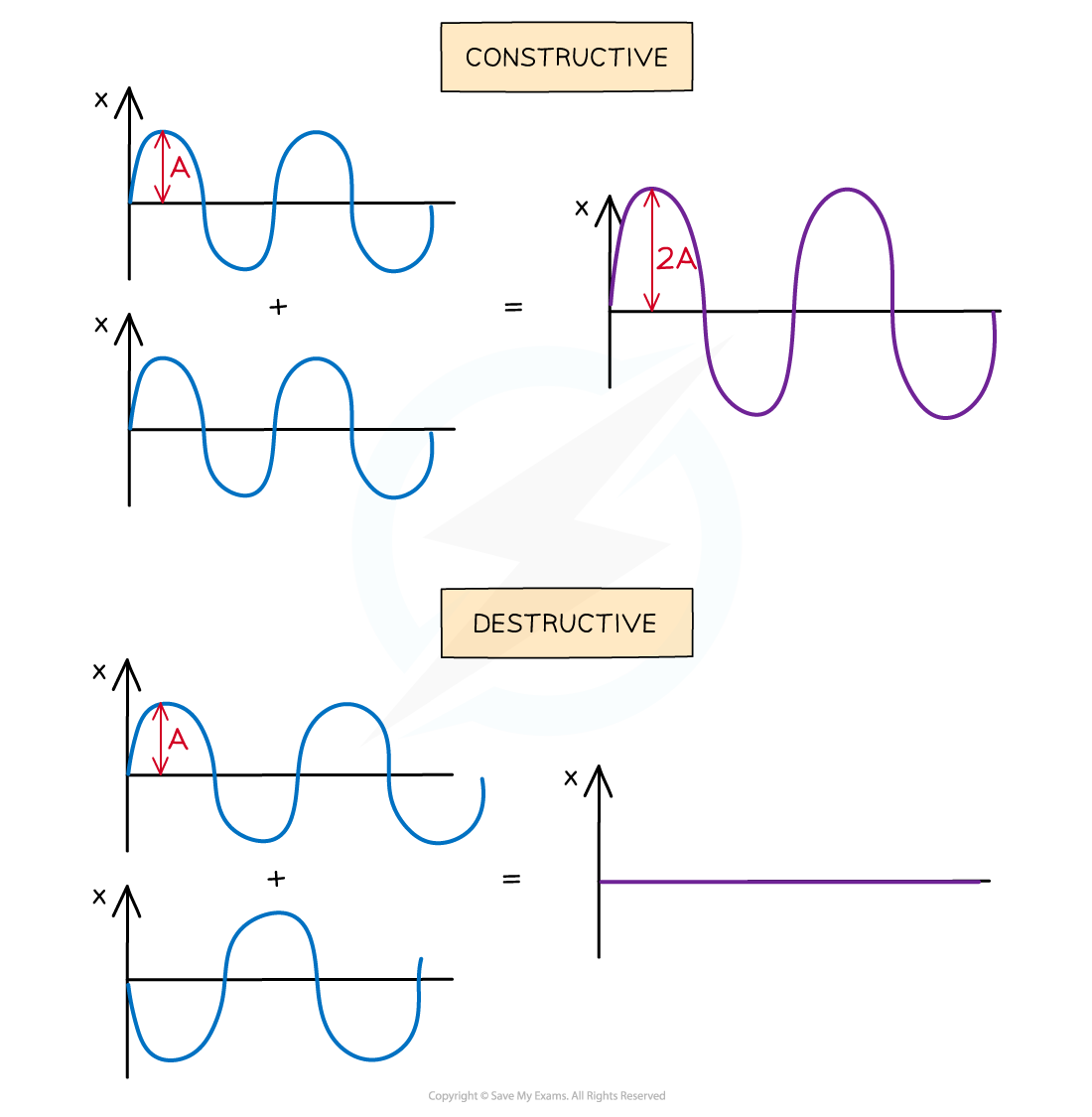
Waves undergo the maximum amount of constructive and destructive interference when they are in phase or antiphase
Coherence
For waves to be coherent they must have:
The same frequency
A constant phase difference
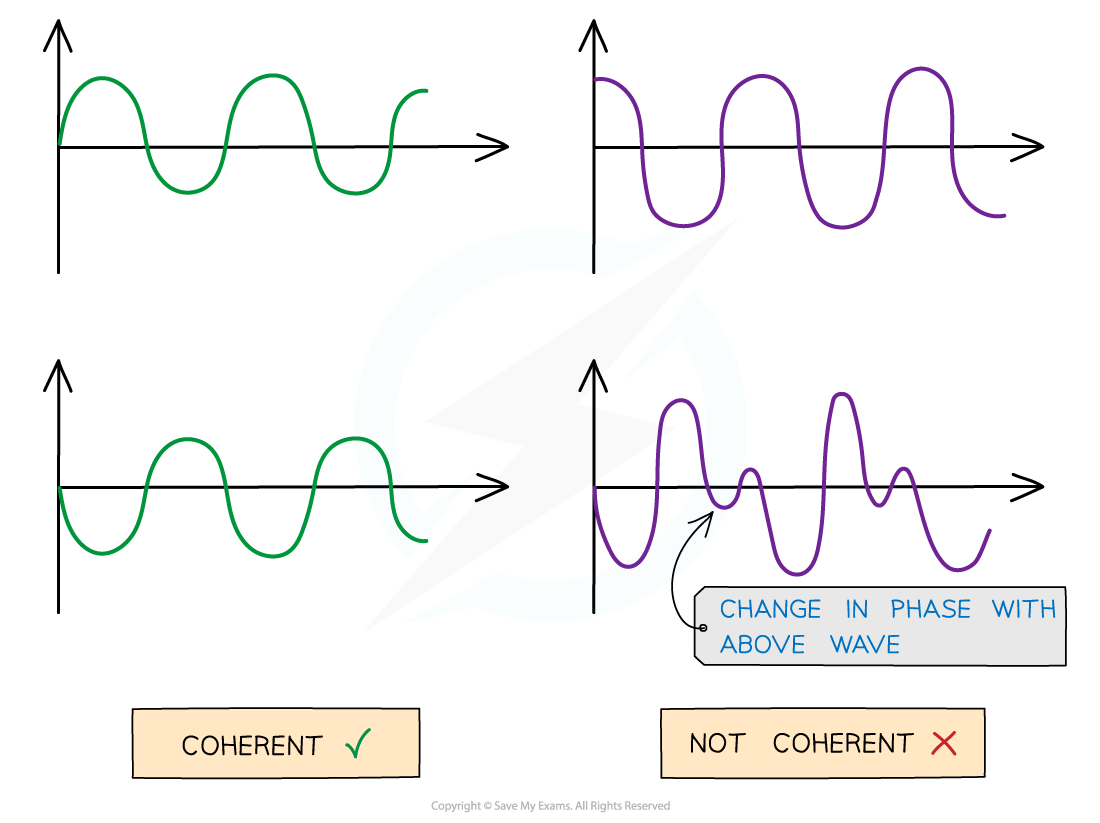
Coherent vs. non-coherent waves. The abrupt change in phase creates an inconsistent phase difference.
At points where two waves are neither in phase nor in antiphase, the resultant amplitude is somewhere in between the two extremes
Examples of interference from coherent light sources are:
Monochromatic laser light
Sound waves from two nearby speakers emitting sound of the same frequency
Constructive & Destructive Interference
Whether waves are in phase or antiphase is determined by their path difference
Path Difference
Path difference is defined as:
The difference in distance travelled by two waves from their sources to the point where they meet
Path difference vs phase difference
Phase difference compares the distance between the phases (peaks and troughs) of waves that are normally travelling parallel to each other at a point
Path difference compares the amount of progress made by waves along a path, so the difference in the distance travelled by the two waves
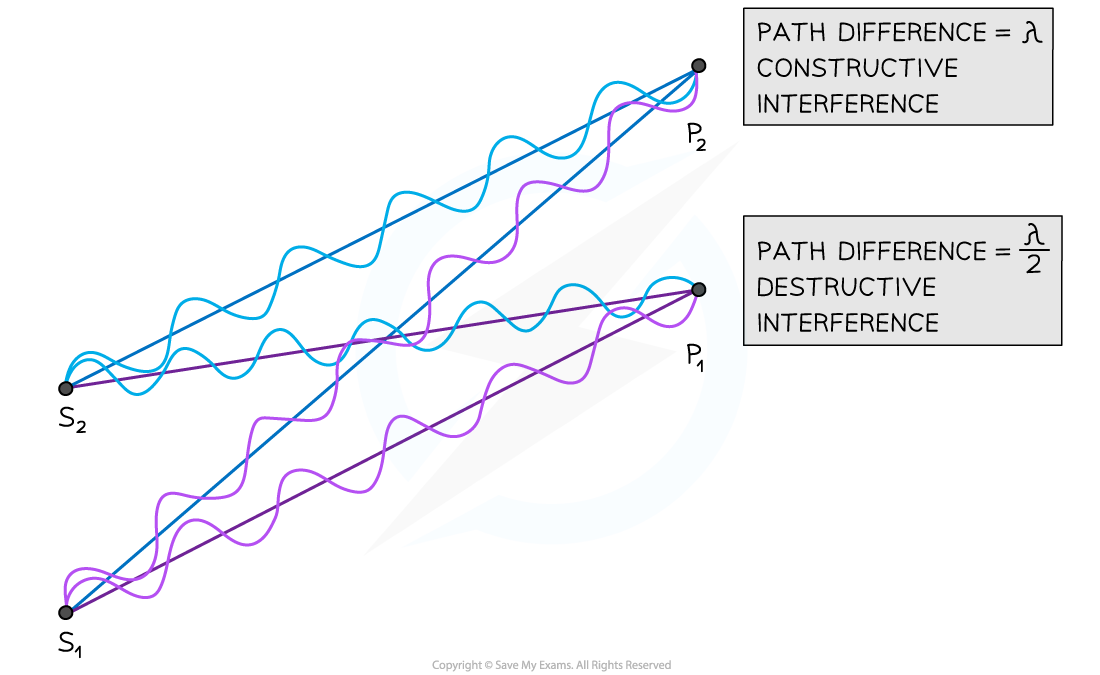
At point P2 the waves have a path difference of a whole number of wavelengths resulting in constructive interference. At point P1 the waves have a path difference of an odd number of half wavelengths resulting in destructive interference
In the diagram above, the number of wavelengths between:
S1 ➜ P1 = 6λ
S2 ➜ P1 = 6.5λ
S1 ➜ P2 = 7λ
S2 ➜ P2 = 6λ
The path difference is:
(6.5λ – 6λ) =
at point P1
(7λ – 6λ) = λ at point P2
Hence:
Destructive interference occurs at point P1
Constructive interference occurs at point P2
Conditions for Constructive and Destructive Interference
In general, for waves emitted by two coherent sources very close together:
The condition for constructive interference is:
path difference =
The condition for destructive interference is:
path difference =
Where:
λ = wavelength of the waves in metres (m)
n = 0, 1, 2, 3... (any other integer)
Path Difference and Wavefront Diagrams
Wavefront diagrams show the interference between waves more clearly
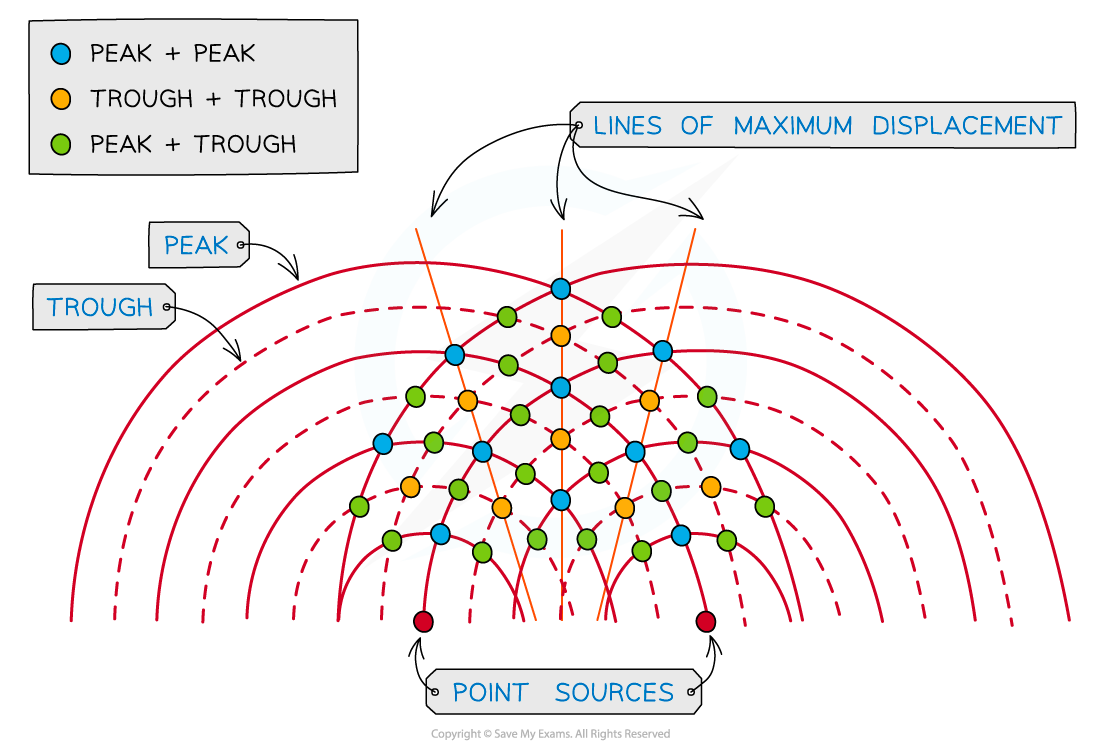
At the blue dot where the peak of two waves meet, constructive interference occurs. At the yellow dot where two troughs meet, constructive interference also occurs. Constructive interference occurs along the lines of maximum displacement. At the green dot, where a peak and a trough meet, destructive interference occurs
On a wavefront diagram, it is possible to count the number of wavelengths to determine whether constructive or destructive interference occurs at a certain point

At point P the waves have a path difference of a whole number of wavelengths, resulting in constructive interference
At point P, the number of crests from:
Source S1 = 4λ
Source S2 = 6λ
So the path difference at P is 6λ – 4λ = 2λ
This is a whole number of wavelengths, hence, constructive interference occurs at point P
Worked Example
The diagram shows the interferences of coherent waves from two-point sources.

Which row in the table correctly identifies the type of interference at points X, Y and Z?
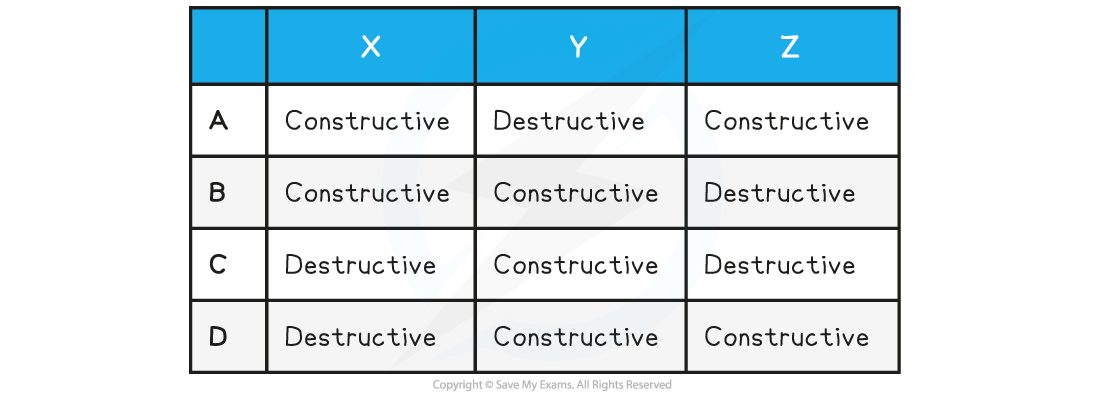
ANSWER: B
At point X:
Both peaks of the waves are overlapping
Path difference = 5.5λ – 4.5λ = λ
This is constructive interference and rules out options C and D
At point Y:
Both troughs are overlapping
Path difference = 3.5λ – 3.5λ = 0
Therefore constructive interference occurs
At point Z:
A peak of one of the waves meets the trough of the other
Path difference = 4λ – 3.5λ = λ / 2
This is destructive interference
Worked Example
The diagram below is a snapshot of overlapping wavefronts resulting from the interference of coherent waves diffracted by two narrow slits S1 and S2.

For each of the points A, B, C, D and E, determine:
The path difference from the sources
The value of n in the path difference formula
Whether they are locations of constructive or destructive interference
Answer:
Step 1: Count the number of wavelengths between each source and the desired point
For example, the number of wavelengths between:
S1 ➜ A = 5λ
S2 ➜ A = 6.5λ
Step 2: Determine the path difference by subtracting the distances of the point from the two sources
For example, path difference at A = (6.5λ – 5λ) = 1.5λ
Step 3: Compare the path difference calculated in Step 2 with the condition for constructive or destructive interference and give the value of n
For example, path difference at A = 1.5λ = (n + ½)λ ➜ n = 1
Step 4: Decide whether the point is a location of constructive or destructive interference
For example, at A, destructive interference occurs
Point A:
Path difference = (6.5λ – 5λ) = 1.5λ
n = 1
Destructive interference
Point B:
Path difference = (5λ – 4λ) = λ
n = 1
Constructive interference
Point C:
Path difference = (2λ – 2λ) = 0
n = 0
Constructive interference
Point D:
Path difference = (5λ – 4.5λ) = 0.5λ
n = 0
Destructive interference
Point E:
Path difference = (4λ – 3λ) = λ
n = 1
Constructive interference
Examiner Tips and Tricks
Remember, interference of two waves can either be:
In phase, causing constructive interference. The peaks and troughs line up on both waves. The resultant wave has double the amplitude
In antiphase, causing destructive interference. The peaks on one wave line up with the troughs of the other. The resultant wave has no amplitude
Think of ‘constructive’ interference as ‘building’ the wave and ‘destructive’ interference as ‘destroying’ the wave.
You are not required to memorise the specific conditions for constructive and destructive interference, as these are given in the data booklet.
You must be able to determine the path difference of waves from two sources (or two narrow slits) at a given point. You can then compare this with the given conditions for constructive and destructive interference, to decide which type of interference occurs at the point you are considering.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
