Diffraction of Waves (DP IB Physics)

Diffraction of Waves

• Diffraction is defined as:

  The spreading out of waves after they pass through a narrow gap or around an obstruction

• Diffraction can occur when waves:

  • pass through an aperture

  • pass around a barrier

Water waves diffract through a gap in a barrier such as in a harbour

Diffraction through an aperture

• When a wave passes through a gap or aperture:

  • The waves spread out so they have curvature 

  • The amplitude of the wave is less because the barrier on either side of the gap absorbs wave energy

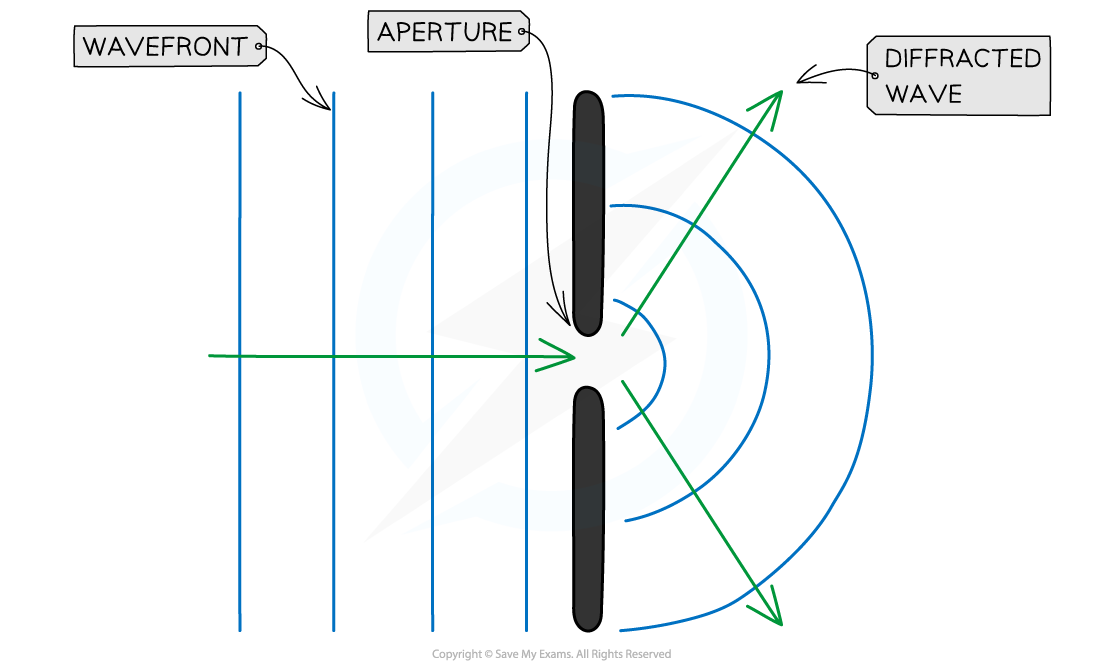
Diffraction causes waves to spread out and become curved after passing through a narrow gap 

• When the wavelength of the wave and the width of the gap is similar then diffraction occurs:

  • When the wavelength is bigger than the gap then more diffraction occurs, so the wave spreads out more after passing through

  • When the wavelength is smaller than the gap then less diffraction occurs, so the wave spreads out less after passing through

• When the wavelength of the wave and the width of the gap are not similar then diffraction does not occur:

  • For gaps that are much smaller than the wavelength of the wave, the wave passes over the gap easily so no diffraction occurs

  • For gaps that are much bigger than the wavelength of the wave, the majority of the wave passes straight through the gap so no diffraction occurs

• As the gap size increases, compared to the wavelength, the amount of curvature on the waves gets less pronounced

Effect of aperture size on diffraction

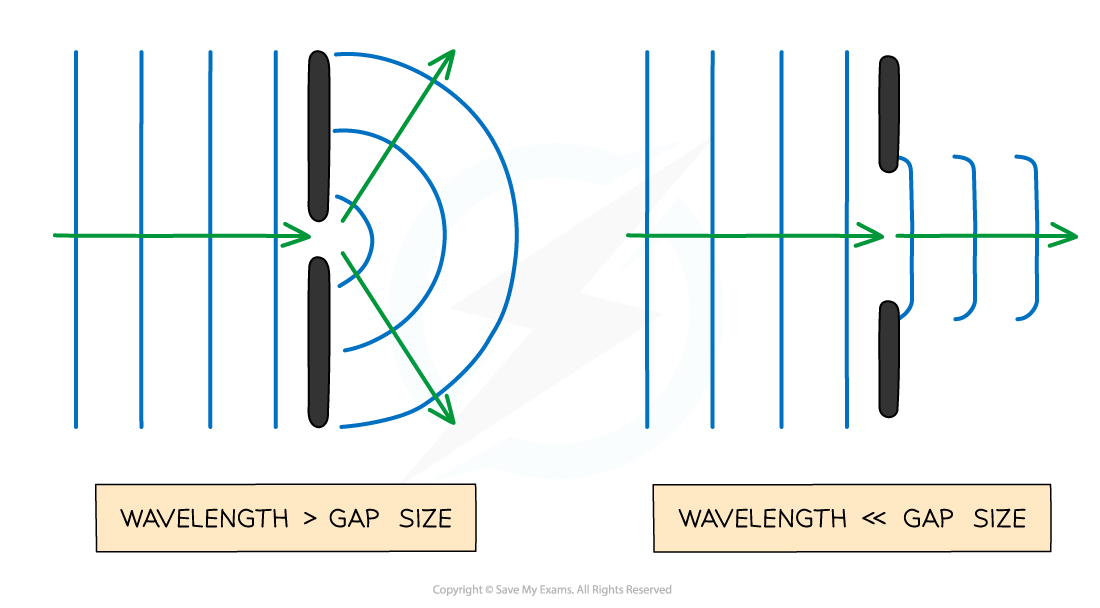
The size of the gap (compared to the wavelength) affects how much the waves spread out when diffracted through a gap

Diffraction around a barrier

• Diffraction can also occur when waves curve around an edge or barrier

  • The waves spread out to fill the gap behind the object

• The extent of this diffraction also depends upon the wavelength of the waves

  • The greater the wavelength then the greater the diffraction

When a wave goes past the edge of a barrier, the waves can curve around it. Shorter wavelengths undergo less diffraction than longer wavelengths

• When the barrier is larger than the wavelength:

  • There is some diffraction around the barrier

  • A lot of incident waves are reflected back towards the source

  • There is a "shadow" region behind the barrier where no wavefronts are present

• When the barrier is the same size as the wavelength:

  • There is more diffraction around the barrier

  • There is a smaller "shadow" region behind the barrier where no wavefronts are present

• When the barrier is smaller than the wavelength:

  • No diffraction occurs around the barrier

  • The "shadow" region behind the barrier is very small

The size of the barrier in relation to the wavelength affects how the waves diffract around it