Phase Angles in Simple Harmonic Motion (SHM) (DP IB Physics) : Revision Note
Phase Angles in Simple Harmonic Motion
Two points on a sine wave, or on different waves, are in phase when they are at the same point in their wave cycle
The angle between their wave cycles is known as the phase angle
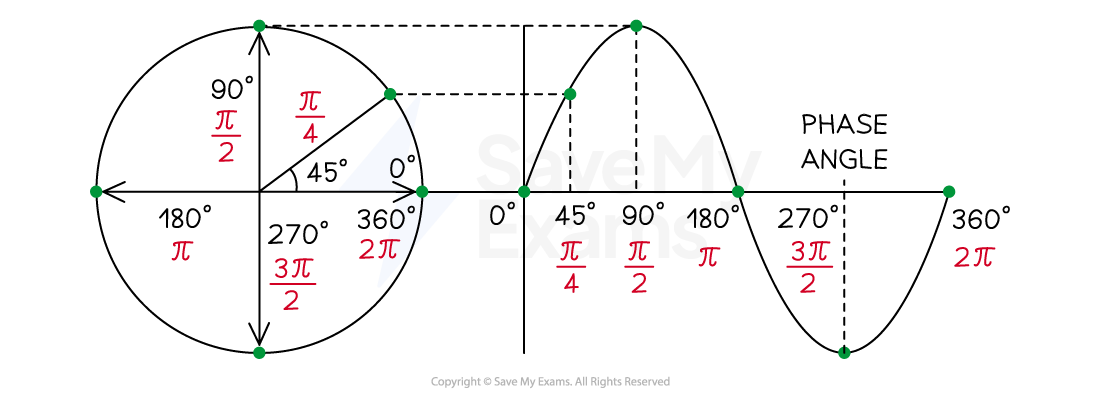
The relationship between a sine wave and phase angle
If an oscillation does not start from the equilibrium position, then it will be out of phase by an angle of
This would be compared to an oscillation which does start from the equilibrium position
The phase angle
of an oscillation (in SHM) is defined as
The difference in angular displacement compared to an oscillator which has a displacement of zero initially (i.e.
when
)
The phase angle can vary anywhere from 0 to 2π radians, i.e. one complete cycle
With the inclusion of the phase angle
, the displacement, velocity and acceleration SHM equations become:
If two bodies in simple harmonic motion oscillate with the same frequency and amplitude, but are out of phase by
, then:
The displacement of the oscillator starting from the equilibrium position is represented by the equation
The displacement of the oscillator which leads by
is represented by the equation
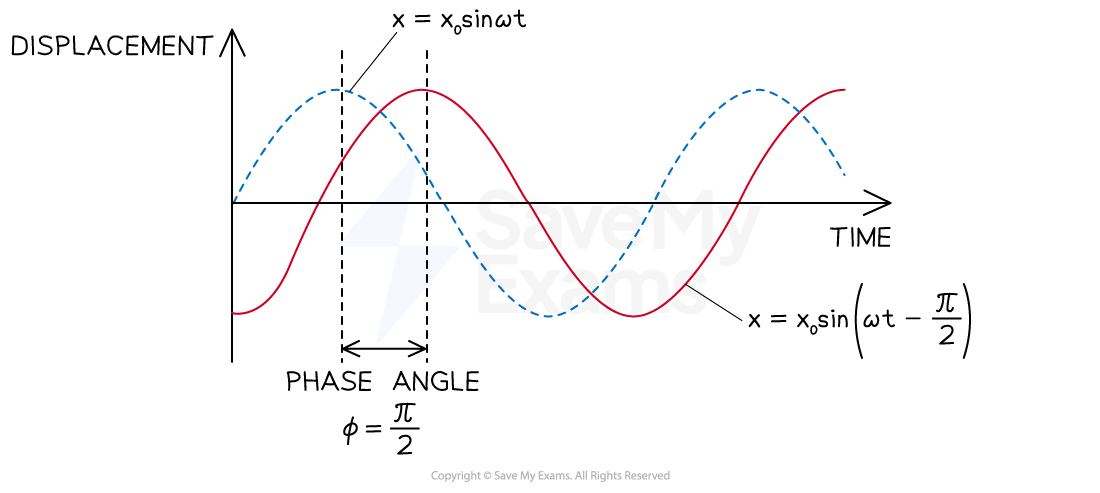
Two oscillators which are out of phase by . The blue-dotted wave represents an oscillator starting from the equilibrium position and the red wave represents an oscillator leading by
When a sine wave leads by a phase angle of
, this is equivalent to the cosine of the wave
Alternatively, a sine wave can be described as a cosine wave that lags by
Notice:
For a wave that lags the phase difference is
For a wave that leads the phase difference is
This is the opposite sign to the one you might think.
To review this concept, use the notes on the Transformation of Trigonometric Functions
How are sine and cosine functions related?
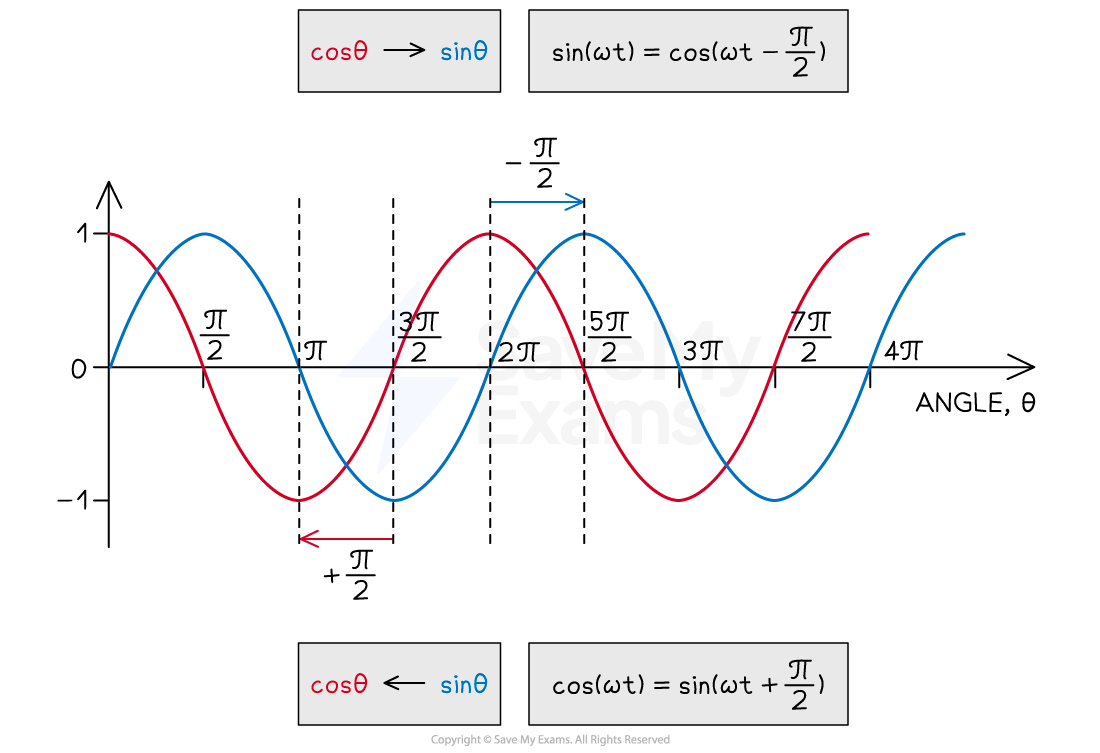
Sine and cosine functions are simply out of phase by radians
The general rules for phase shifts of sine and cosine functions are shown in the table below
Graph | Equation | Phase shift |
|---|---|---|
 | Shifts by | |
 | Shifts by | |
 | Shifts by | |
 | Shifts by |
Worked Example
An object oscillates with simple harmonic motion which can be described by the equation
Which of the following graphs correctly represents this equation?
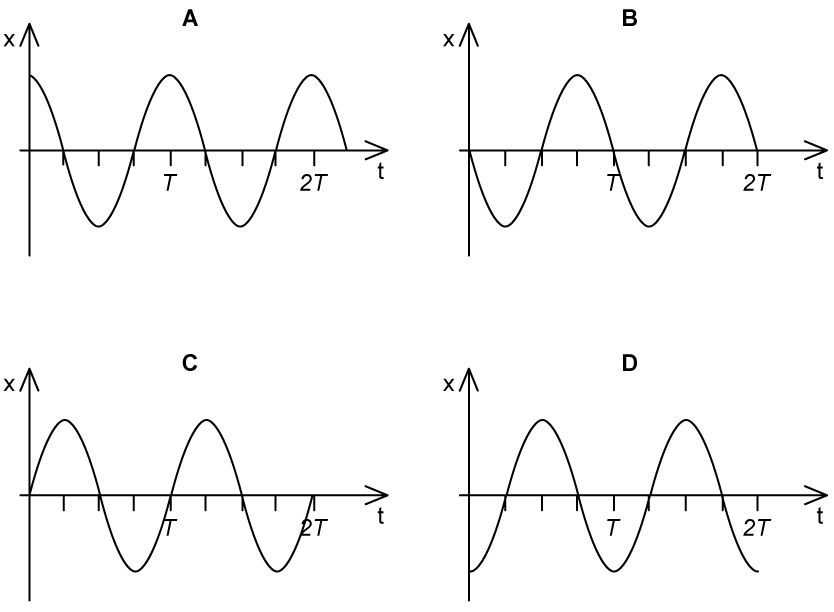
Answer: C
The equation
is equivalent to
This describes an oscillation where
when
Hence, options A & D are not correct
When
is positive, the oscillation will start moving in the
direction
Hence, option B is not correct
Worked Example
A mass attached to a spring is released from a vertical height of at time
. The mass oscillates with a simple harmonic motion of period T.

The graph shows the variation of h with t.
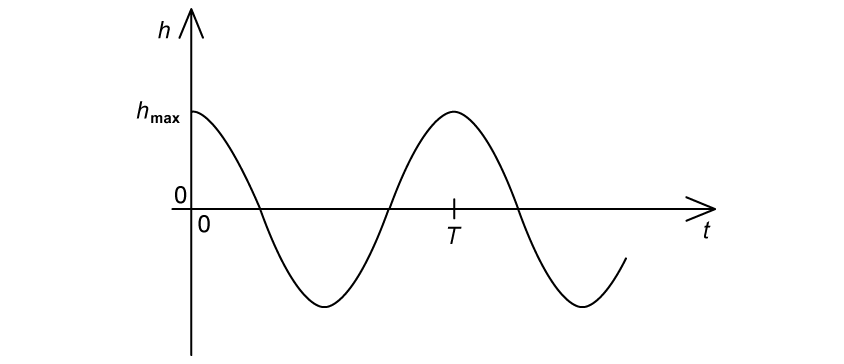
(a) State the equation of motion for this oscillation.
(b) A second mass-spring system is set up and made to oscillate with the same frequency but with a phase angle of . On the graph, sketch the variation of h with t for the second mass-spring system.
Answer:
(a)
The displacement-time equation for an oscillator released from a maximum displacement has the form
or
As the graph is leading a normal sine graph by
Where
and
Angular frequency
is equal to
Therefore, the equation of motion for this oscillation is:
or
(b)
One complete oscillation is equivalent to 2π rad
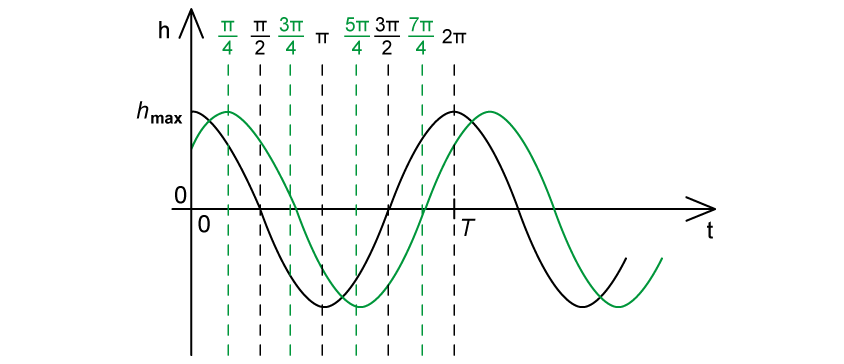
A phase angle of
corresponds to a shift to the right (positive direction)

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
