Calculating Uncertainties (DP IB Physics) : Revision Note
Calculating Uncertainties
There is always a degree of uncertainty when measurements are taken; the uncertainty can be thought of as the difference between the actual reading taken (caused by the equipment or techniques used) and the true value
Uncertainties are not the same as errors
Errors can be thought of as issues with equipment or methodology that cause a reading to be different from the true value
The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate
For example, if the true value of the mass of a box is 950 g, but a systematic error with a balance gives an actual reading of 952 g, the uncertainty is ±2 g
These uncertainties can be represented in a number of ways:
Absolute Uncertainty: where uncertainty is given as a fixed quantity
Fractional Uncertainty: where uncertainty is given as a fraction of the measurement
Percentage Uncertainty: where uncertainty is given as a percentage of the measurement
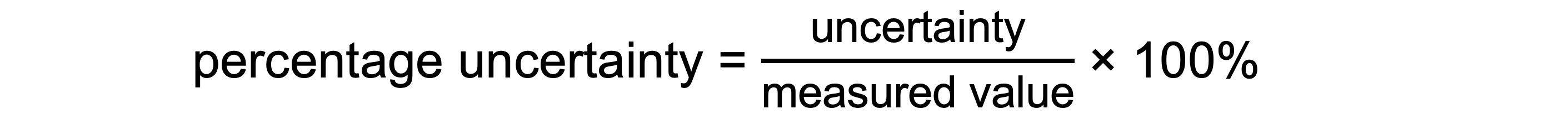
To find uncertainties in different situations:
The uncertainty in a reading: ± half the smallest division
The uncertainty in a measurement: at least ±1 smallest division
The uncertainty in repeated data: half the range i.e. ± ½ (largest - smallest value)
The uncertainty in digital readings: ± the last significant digit unless otherwise quoted
The uncertainty in the natural log of a value: absolute uncertainty in ln(x) =

How to calculate absolute, fractional and percentage uncertainty
Always make sure your absolute or percentage uncertainty is to the same number of significant figures as the reading
Combining Uncertainties
When combining uncertainties, the rules are as follows:
Operation | Example | Propagation Rule |
|---|---|---|
Addition & Subtraction | The sum of the absolute uncertainties | |
Multiplication & Division |
| The sum of the fractional uncertainties |
Power | The magnitude of n times the fractional uncertainty |
Adding / Subtracting Data
Add together the absolute uncertainties

Multiplying / Dividing Data
Add the percentage or fractional uncertainties

Raising to a Power
Multiply the percentage uncertainty by the power

Examiner Tips and Tricks
Remember:
Absolute uncertainties (denoted by Δ) have the same units as the quantity
Percentage uncertainties have no units
The uncertainty in constants, such as π, is taken to be zero
Uncertainties in trigonometric and logarithmic functions will not be tested in the exam, so just remember these rules and you’ll be fine!

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
