Revision NotesExam QuestionsFlashcardsPast Papers
IBPhysicsDPHLRevision NotesThe Particulate Nature of MatterThermal Energy TransfersTemperature & Kinetic Energy

Temperature & Kinetic Energy (DP IB Physics)

Revision Note

Katie M

Author

Katie M

Last updated

DP Physics: HLDP Physics: SL

Temperature & Kinetic Energy

  • Particles in gases usually have a range of speeds

  • The average kinetic energy of the particles Ek can be calculated using the equation

E subscript k space equals space 3 over 2 k subscript B T

  • Where:

    • Ek = average kinetic energy of the particles in joules (J)

    • kB = 1.38 × 10–23 J K–1 (Boltzmann's constant)

    • T = absolute temperature in kelvin (K)

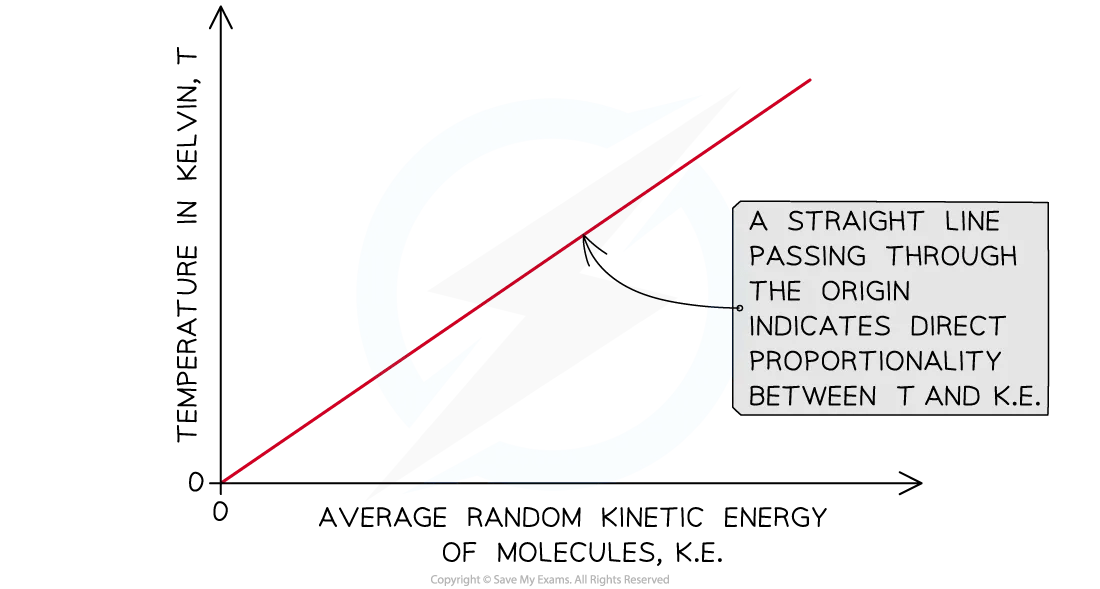
  • This tells us that the absolute temperature of a body is directly proportional to the average kinetic energy of the molecules within the body

Relationship between absolute temperature and average random kinetic energy of molecules

Graph of Absolute Temperature against Kinetic Energy of Molecules, for IB Physics Revision Notes

Worked Example

The surface temperature of the Sun is 5800 K and contains mainly hydrogen atoms.

Calculate the average speed of the hydrogen atoms, in km s−1, near the surface of the Sun.

Answer:

Step 1: List the known quantities

  • Temperature, T = 5800 K

  • Mass of a hydrogen atom = mass of a proton, mp = 1.673 × 10−27 kg

  • Boltzmann constant, kB = 1.38 × 10−23 J K−1

Step 2: Equate the equations relating kinetic energy with temperature and speed

  • Average kinetic energy of a molecule:  E subscript k space equals space 3 over 2 k subscript B T

  • Kinetic energy:  E subscript k space equals space 1 half m v squared

3 over 2 k subscript B T space equals space 1 half m subscript p v squared

Step 3: Rearrange for average speed and calculate

fraction numerator 3 k subscript B T over denominator m subscript p end fraction space equals space v squared

v space equals space square root of fraction numerator 3 k subscript B T over denominator m subscript p end fraction end root space equals space square root of fraction numerator 3 cross times open parentheses 1.38 cross times 10 to the power of negative 23 end exponent close parentheses cross times 5800 over denominator 1.673 cross times 10 to the power of negative 27 end exponent end fraction end root

Average speed:  v = 11 980 m s−1 = 12 km s−1

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Temperature ScalesNext:Internal Energy
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.