Apparent Brightness & Luminosity (DP IB Physics)

Apparent Brightness & Luminosity

• The apparent brightness b of a star is defined as:

  The intensity of radiation received on Earth from a star 

• Apparent brightness is measured in watts per metre squared (W m⁻²)

• The apparent brightness of a star depends on two main factors:

  • How much light the star emits

  • How far away the star is (more distant stars are usually fainter than nearby stars)

• How much light the star emits is given by the luminosity L of the star, which is defined as:

  The total power output of radiation emitted by a star

• Luminosity is measured in units of watts (W)

What is the difference between apparent brightness and luminosity?

The luminosity is the total power output of the star, whereas the apparent brightness is what is measured on Earth

• Knowing the luminosity and apparent brightness of a star is useful because it allows us to determine how far away it is from the Earth

• This is because

  • Luminosity tells us how bright the star is at its surface

  • Apparent brightness tells us how bright the star is as observed from the Earth

• Therefore, by the time the radiation from the distant star reaches the Earth, it will have spread out over a very large area

  • This means the intensity of the radiation detected on Earth will only be a fraction of the value of the star's luminosity

Inverse Square Law of Radiation

• A light source which is further away appears fainter because the light it emits is spread out over a greater area

• The moment the light leaves the surface of the star, it begins to spread out uniformly through a spherical shell

  • The surface area of a sphere is equal to 4πr²

• The radius r of this sphere is equal to the distance d between the star and the Earth

  • By the time the radiation reaches the Earth, it has been spread over an area of 4πd²

• This is called following an inverse square law

  • This phrase can be used to refer to any quantity whose intensity reduces by a factor equal to the square of the distance to the observer (e.g. the intensity of ionising radiation follows an inverse square law)

• The inverse square law of radiation can be written as:

• Where:

  • b = apparent brightness, or observed intensity on Earth (W m⁻²)

  • L = luminosity of the source (W)

  • d = distance between the star and the Earth (m)

• This equation assumes:

  • The power from the star radiates uniformly through space

  • No radiation is absorbed between the star and the Earth

• This equation tells us:

  • For a given star, the luminosity is constant

  • The intensity of the emitted light follows an inverse square law

  • For stars with the same luminosity, the star with the greater apparent brightness is closer to the Earth

Inverse square law of radiation

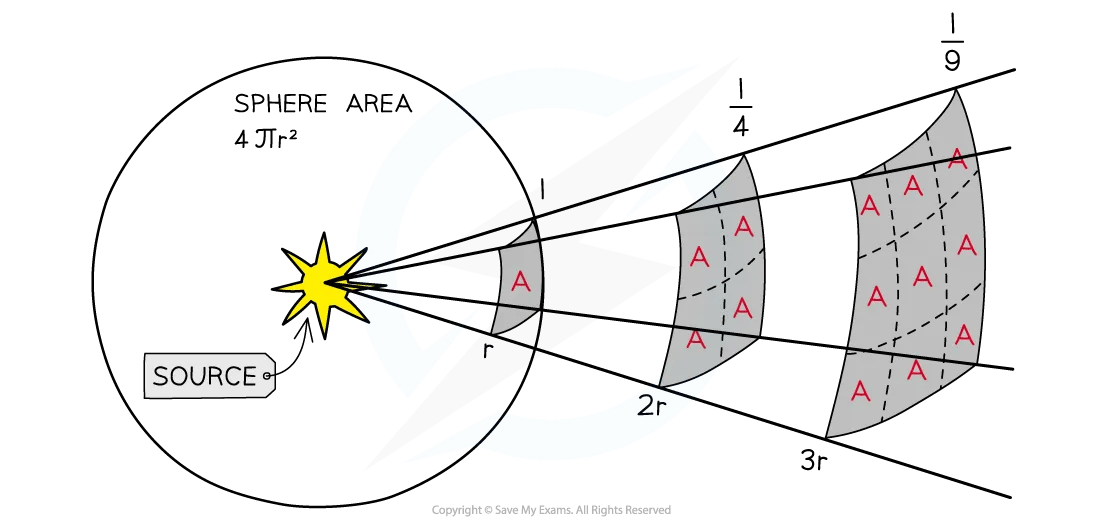
When the light is twice as far away, it has spread over four times the area, hence the intensity is four times smaller