Gravitational Potential Energy (DP IB Physics) : Revision Note
Gravitational Potential Energy
Gravitational potential energy is the energy stored in a mass due to its position in a gravitational field
If a mass is lifted up, it will gain gravitational potential energy
If a mass falls, it will lose gravitational potential energy
The equation for gravitational potential energy when close to the surface of the Earth is:
Where:
ΔEp = gravitational potential energy (J)
m = mass (kg)
g = gravitational field strength (9.8 N kg–1)
Δh = change in height (m)
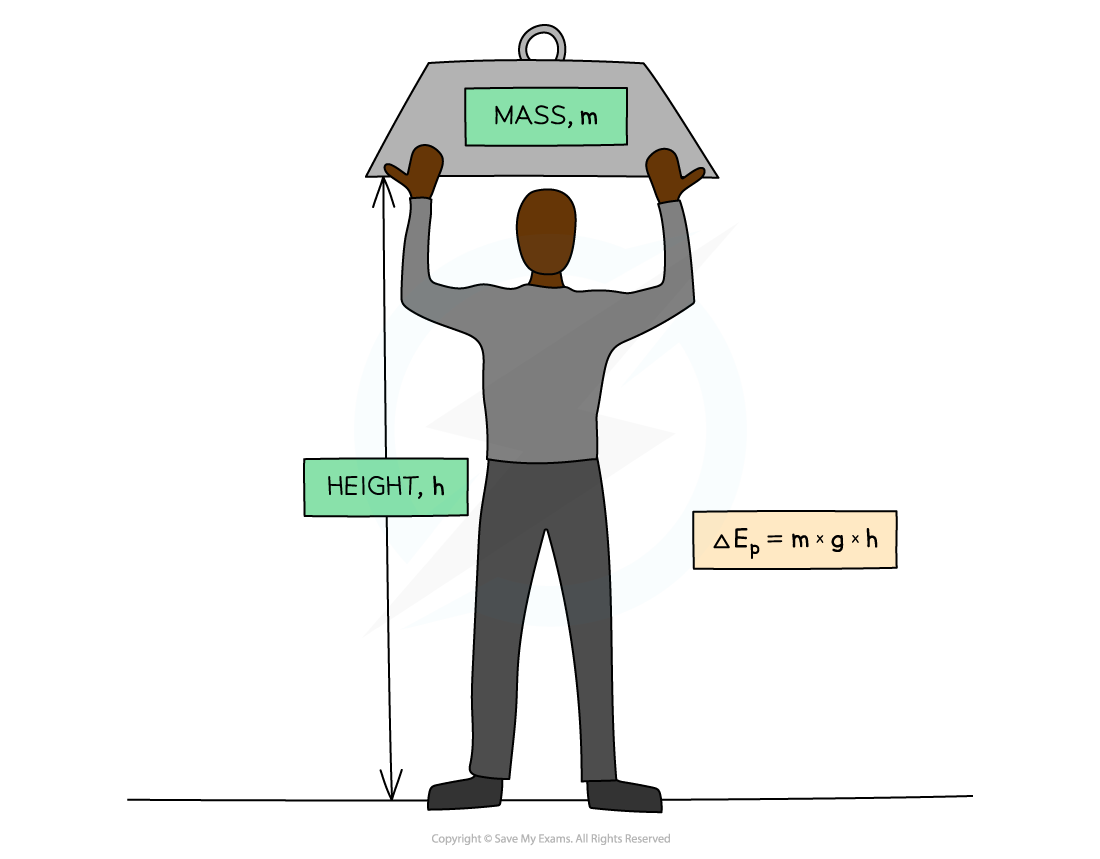
Gravitational potential energy: The energy an object has when lifted up
The potential energy on the Earth’s surface at ground level is usually taken to be equal to zero
However, any position can be taken as zero if you are calculating the change in gravitational potential energy
This equation is only relevant for energy changes in a uniform gravitational field (such as near the Earth’s surface)
A different potential energy is used in the gravitational fields topic, because the field is no longer uniform outside of the Earth's surface
Gravitational Potential Energy vs Height
The two graphs below show how the gravitational potential energy changes with height for a ball being thrown up in the air and then falling down (ignoring air resistance)

Graphs showing the linear relationship between gravitational potential energy and height
Since the graphs are straight lines, gravitational potential energy and height are said to have a linear relationship
These graphs would be identical for gravitational potential energy against time instead of height
Worked Example
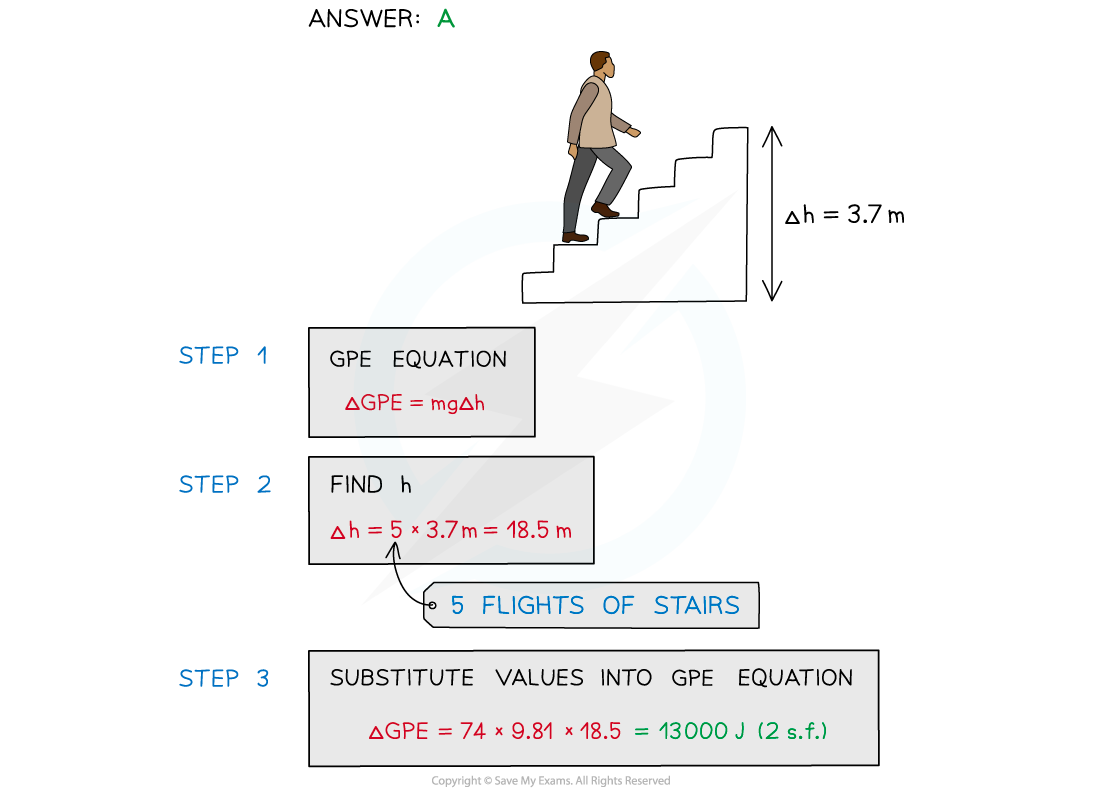
To get to his apartment a man has to climb five flights of stairs.
The height of each flight is 3.7 m and the man has a mass of 74 kg.
What is the approximate change in the man's gravitational potential energy during the climb?
A. 13 000 J
B. 2700 J
C. 1500 J
D. 12 500 J
Examiner Tips and Tricks
Gravitational potential energy is often shortened to GPE for ease. In your equations, you should stick to the correct symbol, which is

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
