Revision NotesExam QuestionsFlashcardsPast Papers
IBPhysicsDPHLRevision NotesSpace, Time & MotionWork, Energy & PowerElastic Potential Energy

Elastic Potential Energy (DP IB Physics)

Revision Note

Ashika

Author

Ashika

Last updated

DP Physics: HLDP Physics: SL

Elastic Potential Energy

  • Elastic potential energy is defined as

    The energy stored within a material (e.g. in a spring) when it is stretched or compressed

  • Therefore, for a material obeying Hooke’s Law, elastic potential energy is equal to:

E subscript H space equals space 1 half k increment x squared

  • Where:

    • k = spring constant of the spring (N m–1)

    • Δx = extension of the spring (m)

  • This can also be written as:

E subscript H space equals space 1 half F increment x

  • Where:

    • F = restoring force (N)

  • This force is the same restoring force as in Hooke's law: F space equals space k increment x

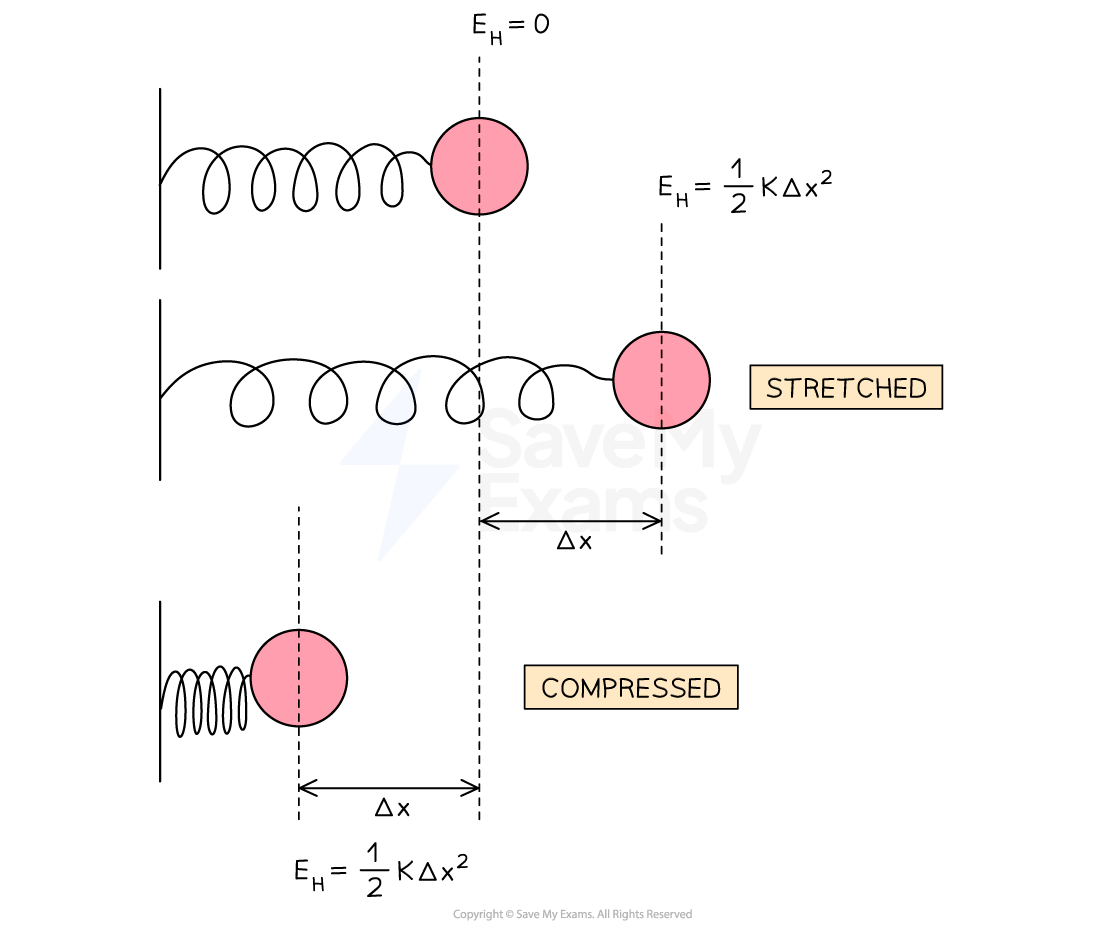
1-3-6-elastic-potential-energy-spring

A spring that is stretched or compressed has elastic potential energy

  • It is very dangerous if a wire under large stress suddenly breaks

  • This is because the elastic potential energy of the strained wire is converted into kinetic energy

E subscript H space equals space E subscript K 

1 half k increment x squared space equals space 1 half m v squared

v space proportional to space increment x

  • This equation shows

    • The greater the extension of a wire Δx the greater the speed v it will have when it breaks

Worked Example

A car’s shock absorbers make a ride more comfortable by using a spring that absorbs energy when the car goes over a bump. One of these springs, with a spring constant of 50 kN m–1 is fixed next to a wheel and compressed a distance of 10 cm.

Calculate the energy stored by the compressed spring.

Answer:

Step 1: List the known values

  • Spring constant, k = 50 kN m–1 = 50 × 103 N m–1

  • Compression, x = 10 cm = 10 × 10–2 m

Step 2: Substitute the values into the elastic potential energy equation

E subscript H space equals 1 half space cross times space open parentheses 50 space cross times space 10 cubed close parentheses space cross times space open parentheses 10 space cross times space 10 to the power of negative 2 end exponent close parentheses squared space equals space 250 space straight J

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Gravitational Potential EnergyNext:Conservation of Mechanical Energy
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.