Rotational Kinetic Energy (DP IB Physics: HL): Revision Note

Rotational Kinetic Energy

• A body moving with linear velocity has an associated linear kinetic energy given by

$E_k=\frac{1}{2}m{v}^2$

$E_k=\frac{p^2}{2m}$

• Similarly, a rotating body with angular velocity has an associated rotational kinetic energy given by

$E_k=\frac{1}{2}I{\omega }^2$

$E_k=\frac{L^2}{2I}$

• Where:

  • $E_k$ = rotational kinetic energy (J)

  • $I$ = moment of inertia (kg m²)

  • $\omega$ = angular velocity (rad s⁻¹)

  • $L$ = angular momentum (kg m² s⁻¹)

Rolling without slipping

• Circular objects, such as wheels, are made to move with both linear and rotational motion

  • For example, the wheels of a car, or bicycle rotate causing it to move forward

• Rolling motion without slipping is a combination of rotating and sliding (translational) motion

• When a disc rotates:

  • Each point on the disc has a different linear velocity depending on its distance from the centre $\left(v\propto r\right)$

  • The linear velocity is the same at all points on the circumference 

• When a disc slips, or slides:

  • There is not enough friction present to allow the object to roll

  • Each point on the object has the same linear velocity

  • The angular velocity is zero

• So, when a disc rolls without slipping:

  • There is enough friction present to initiate rotational motion allowing the object to roll

  • The point in contact with the surface has a velocity of zero

  • The centre of mass has a velocity of $v=\omega r$

  • The top point has a velocity of $2v$ or $2\omega r$

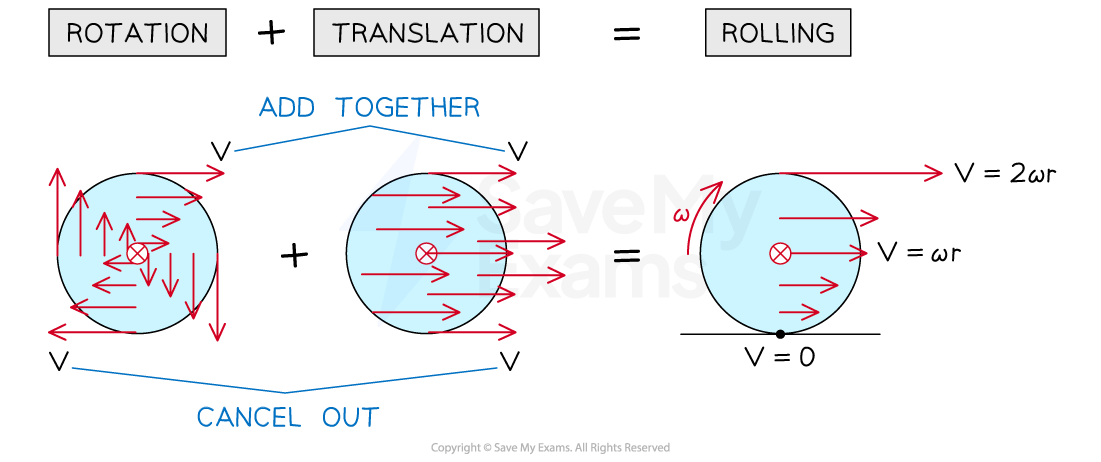
Rolling motion is a combination of rotational and translational motion. The resultant velocity at the bottom is zero and the resultant velocity at the top is 2v

Rolling down a slope

• Another common scenario involving rotational and translational motion is an object (usually a ball or a disc) rolling down a slope

• At the top of the slope, a stationary object will have gravitational potential energy equal to

$E_p=mg∆h$

• As the object rolls down the slope, the gravitational potential energy will be transferred to both translational (linear) and rotational kinetic energy

• At the bottom of the slope, the total kinetic energy of the object will be equal to

$E_{Ktotal}=\frac{1}{2}m{v}^2+\frac{1}{2}I{\omega }^2$

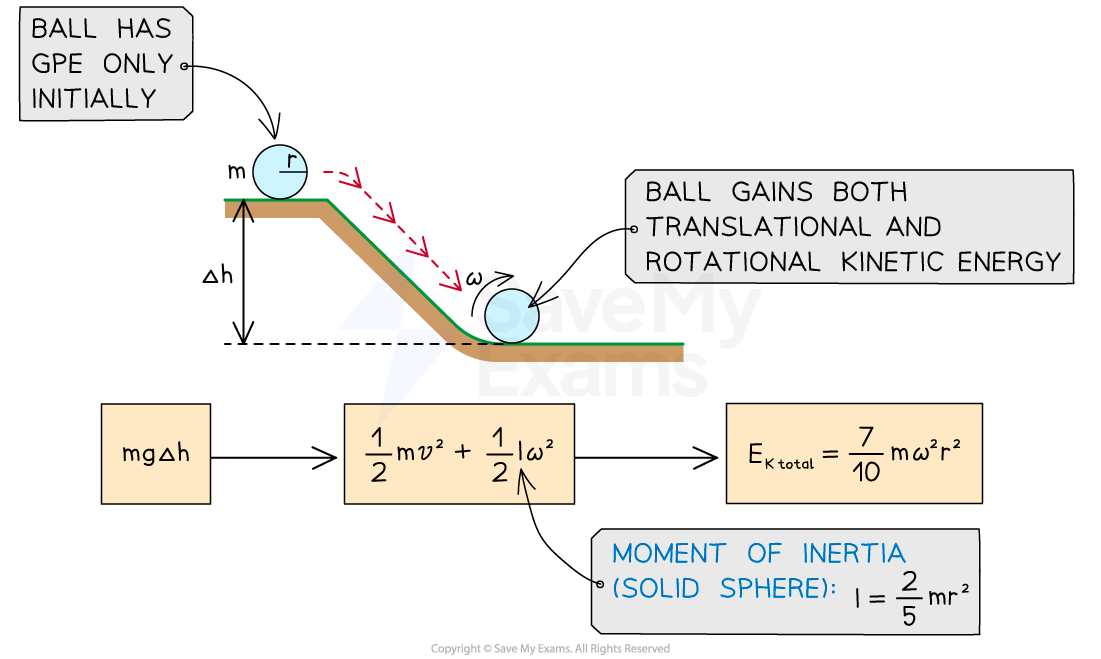
• The linear or angular velocity can then be determined by

  • Equating $E_p$ and $E_{Ktotal}$

  • Using the equation for the moment of inertia of the object

  • Using the relationship between linear and angular velocity $v=\omega r$

• For example, for a ball (a solid sphere) of mass m and radius r, its moment of inertia is

$I=\frac{2}{5}m{r}^2$

• Equating the equations for $E_p$ and $E_{Ktotal}$ and simplifying gives

$mg∆h=\frac{1}{2}m{\left(\omega r\right)}^2+\frac{1}{2}\left(\frac{2}{5}m{r}^2\right){\omega }^2$

$mg∆h=\frac{1}{2}m{\omega }^2{r}^2+\frac{1}{5}m{\omega }^2{r}^2$

$mg∆h=\frac{7}{10}m{\omega }^2{r}^2$