Angular Momentum (DP IB Physics) : Revision Note
Angular Momentum
Angular momentum is the rotational equivalent of linear momentum, which is defined by mass × velocity, or
Therefore, angular momentum
is defined by
Where:
= angular momentum (kg m2 rad s−1)
= moment of inertia (kg m2)
= angular velocity (rad s−1)
Angular Momentum of a Point Mass
The moment of inertia of a rotating point mass m which is a distance r from an axis of rotation is equal to
The angular velocity of the point mass is given by
Therefore, the angular momentum of the point mass is equal to
Worked Example
A horizontal rigid bar is pivoted at its centre so that it is free to rotate. A point particle of mass 3M is attached at one end of the bar and a container is attached at the other end, both are at a distance of R from the central pivot.
A point particle of mass M moves with velocity v at right angles to the rod as shown in the diagram.

The particle collides with the container and stays within it as the system starts to rotate about the vertical axis with angular velocity ω.
The mass of the rod and the container are negligible.
Write an expression for the angular momentum of the system about the vertical axis:
(a) just before the collision, in terms of M, v and R
(b) just after the collision, in terms of M, R and ω
Answer:
(a) Just before the collision:
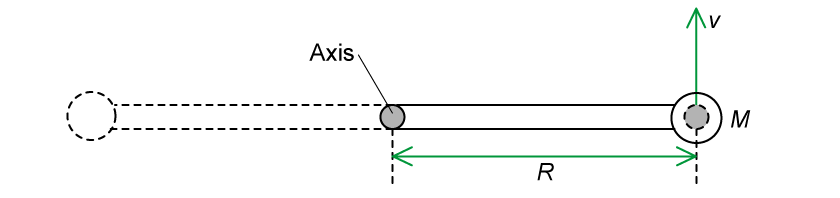
Angular momentum is equal to:
The moment of inertia of a point particle is
Linear velocity is related to angular velocity by
The rod, container and 3M mass are all stationary before the collision, so we only need to consider the angular momentum of the point particle
Where:
Mass of the particle,
Distance of the particle from the axis,
Angular velocity of the particle,
Therefore, the angular momentum of the system before the collision is:
(b) After the collision:
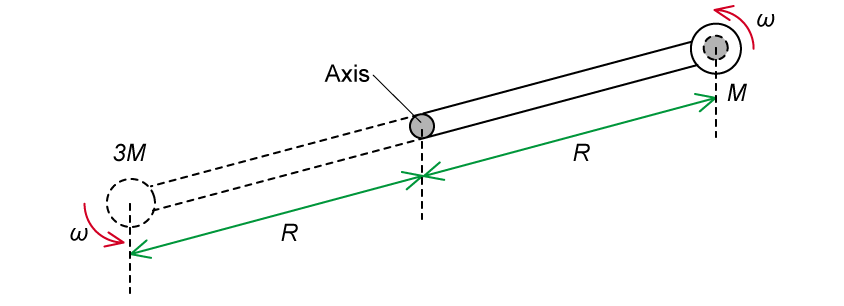
The whole system rotates with an angular velocity of ω
We are considering the rod and the container as massless, so we only need to consider the angular momentum of the two masses M and 3M
Therefore, the angular momentum of the system after the collision is:
Examiner Tips and Tricks
You should know that objects travelling in straight lines can have angular momentum - just make sure you understand that it all depends on the position of the object in relation to the axis of rotation being considered
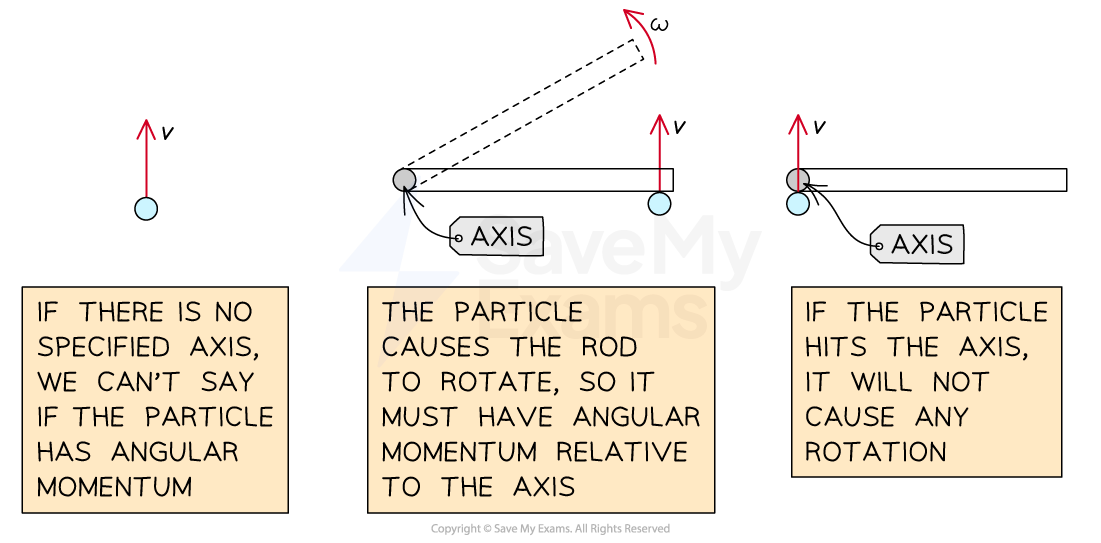
Conservation of Angular Momentum
As with linear momentum, angular momentum is always conserved
The principle of conservation of angular momentum states:
The total angular momentum of a system always remains constant, unless acted upon by a net resultant torque
This conservation law has many real-world applications, for example:
a person on a spinning chair spins faster while their arms and legs are contracted, and slower while extended
objects in elliptical orbits travel faster nearer the object they orbit and slower when further away
ice skaters can change their rotation velocity by extending or contracting their arms
tornados spin faster as their radius decreases
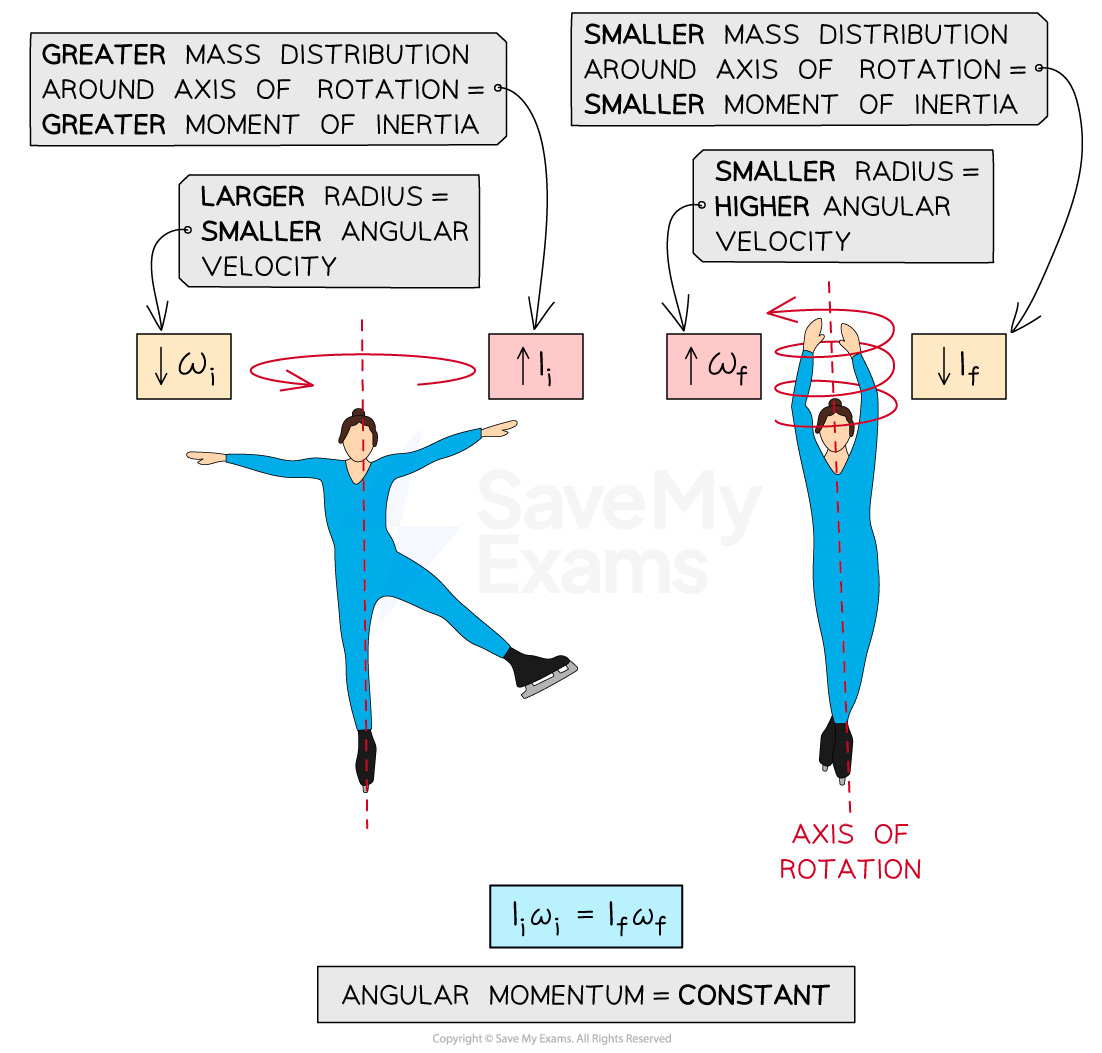
Ice skaters can change their moment of inertia by extending or contracting their arms and legs. Due to conservation of angular momentum, this allows them to spin faster or slower
Problems involving a constant total angular momentum can be solved using the equation:
Where:
= initial moment of inertia (kg m2)
= initial angular velocity (rad s−1)
= final moment of inertia (kg m2)
= final angular velocity (rad s−1)
Worked Example
The diagram shows the different positions of a diver between jumping off a springboard and entering the water.
During their fall, the diver pulls their arms and legs into a tight tuck position while in the air and straightens them before entering the water.
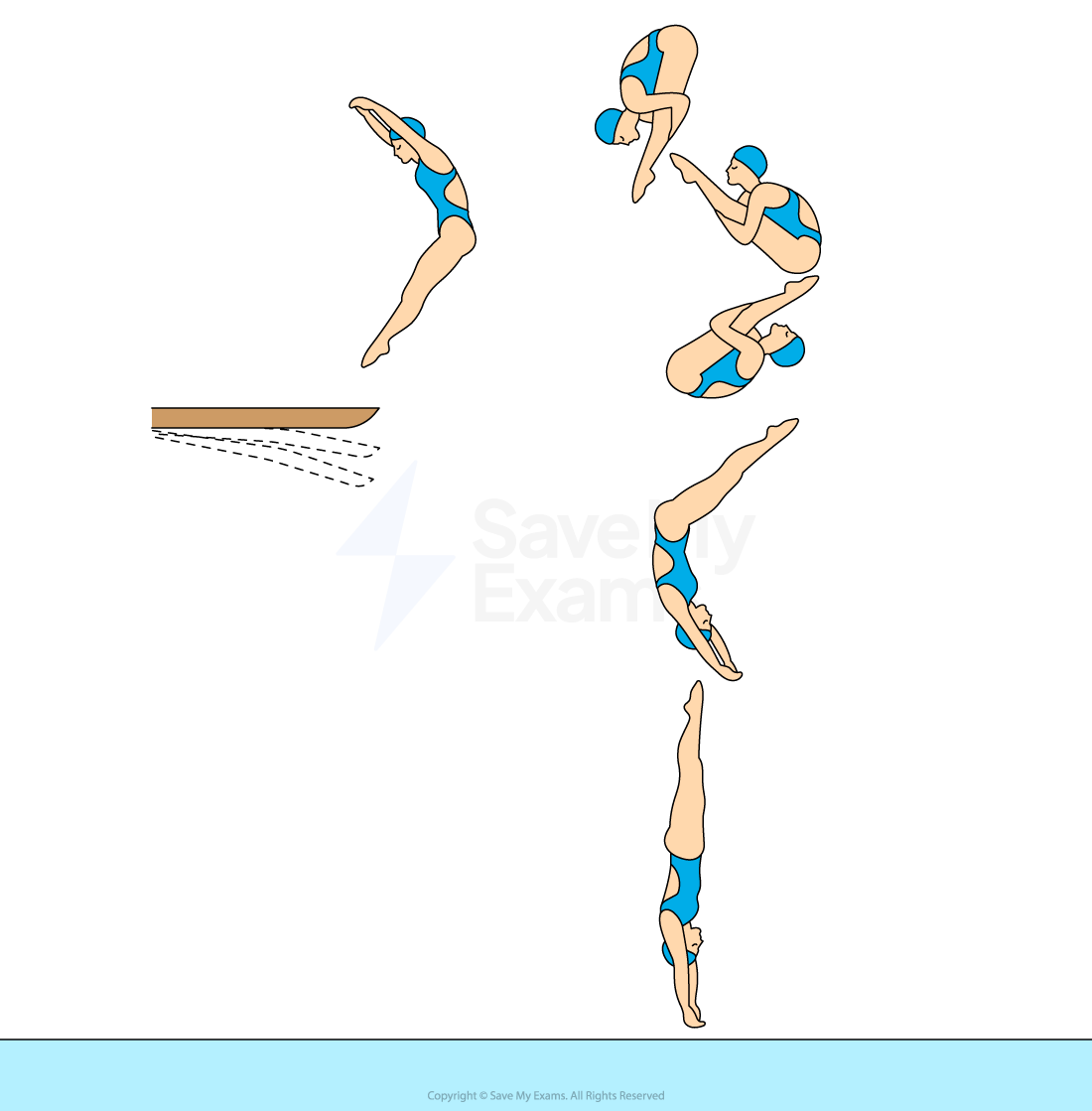
Which row correctly describes the changes to the diver's moment of inertia and angular velocity as they bring their limbs closer to their body?
| moment of inertia | angular velocity |
A. | increases | increases |
B. | decreases | increases |
C. | increases | decreases |
D. | decreases | decreases |
Answer: B
After the diver leaves the springboard, there is no longer a resultant torque acting on them
This means their angular momentum remains constant throughout the dive
Due to the conservation of angular momentum:
When the diver tucks their arms and legs in closer to their body, they decrease their moment of inertia
This eliminates options A & C
Therefore, to conserve angular momentum, when the diver's moment of inertia decreases, their angular velocity must increase
Worked Example
A spherical star of mass M and radius R rotates about its axis. The star explodes, ejecting mass in space radially and symmetrically. The remaining star is left with a mass of and a radius of
.
Calculate the ratio of the star’s final angular velocity to its initial angular velocity.
The moment of inertia of a sphere is
Answer:
Before the star explodes:
Initial moment of inertia,
Initial angular velocity =
After the star explodes:
Final moment of inertia,
Final angular velocity =
From the conservation of angular momentum:
Therefore, the ratio of the star’s final angular velocity to its initial angular velocity is:

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
