IBPhysicsDPHLRevision NotesSpace, Time & MotionGalilean & Special RelativityLorentz Transformations

Lorentz Transformations (DP IB Physics: HL): Revision Note

Written by: Ashika

Reviewed by: Caroline Carroll

Updated on 2 July 2026

Lorentz Transformation Equations

To relate measurements from one reference frame to another in Galilean relativity, we used Galilean transformations
However, Galilean transformations can no longer be used to describe distances, times and speeds for objects travelling close to the speed of light
Einstein's postulates of special relativity lead to the Lorentz transformation equations for the coordinates of an event in two inertial reference frames

The Lorentz Factor

Lorentz transformations are a correction of the Galilean transformations for speeds close to the speed of light, by multiplying by a scaling factor called the Lorentz factor, $γ$

$γ = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$

As v will always be less than c ( since nothing can travel faster than the speed of light), this means that $γ$ will always be greater than 1
This is especially important for time dilation and length contraction

Lorentz Transformation Equations

Again we have the reference frame S measuring with co-ordinates (x, y, t), and S' with co-ordinates (x', y', t')
Person F is moving away from Person E in their rocket ship at speed v which is close to the speed of light c
- Person E is a stationary observer on Earth
Both Person E and Person F witness a loud bang some distance away
- Person F measures the loud bang to be a distance x' away
- Person E measures the loud bang to be a distance x = γ(x' + vt') away

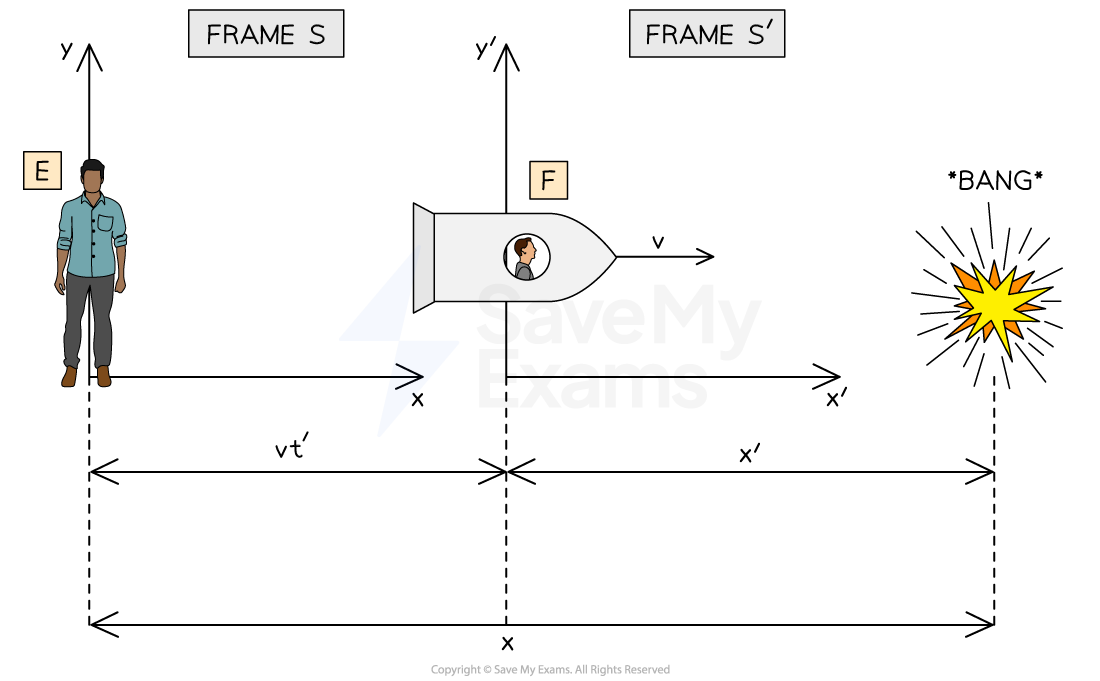
People E measures the loud bang to be at a different distance to person F

However, motion is relative
According to Person F, they are stationary and Person E is moving away from them at a velocity v in the opposite direction
So from Person F's point of view:
- Person E's velocity is -v
- Therefore, Person F measures the bang to happen at a distance x' = γ(x - vt) away
But, the time the bang happens is not the same in both frames of reference! t ≠ t'
These are the exact same equations as the Galilean transformation equations, just with the added Lorentz factor
In summary, the Lorentz equations from frame S → S' are:

$x' = γ (x - v t)$

$t' = γ (t - \frac{v x}{c^{2}})$

Where:
- (x, y, z, t) = the co-ordinates measured from one reference frame
- (x', y', z', t') = the co-ordinates measured from another reference frame moving at speed v relative to it

Galilean vs. Lorentz Transformations

Lorentz (v ≈ c)	Galilean (v << c)
$x' = γ (x - v t)$	$x' = x - v t$
$x = γ (x' + v t')$	$x = x' + v t$
$t' = γ (t - \frac{v x}{c^{2}})$	$t' = t$
$t = γ (t' + \frac{v x'}{c^{2}})$	$t = t'$
$y = y'$	$y = y'$
$z = z'$	$z = z'$

Notice that time is different between reference frames t and t' for objects travelling close to the speed of light, whilst in Galilean transformations, time was absolute (it doesn't change) between reference frames

Worked Example

A rocket of proper length 150 m moves to the right with speed 0.91c relative to the ground.

A probe is released from the back of the rocket at speed 0.45c relative to the rocket.

Determine the time it takes the probe to reach the front of the rocket according to an observer

(a) At rest in the rocket.

(b) At rest on the ground.

Answer:

(a)

Step 1: List the known quantities

Length of the rocket, l = 150 m
Speed of the probe, v' = 0.40c

Step 2: Analyse the situation

In the reference frame of an observer at rest in the rocket, they are stationary
Therefore, the probe travels at a constant speed 0.45c across the full length of the rocket of 150 m

$t' = \frac{l}{v'} = \frac{150}{0.45 c} = \frac{150}{0.45 \times (3 \times 10^{8})}$

$t' = 1.11 \times 10^{- 6} s$

t' and v' are used because they are the times and velocity of the moving object in the reference frame of the observer at rest

(b)

Step 1: List the known quantities

Length of the rocket, l = 150 m
Speed of the rocket, v = 0.91c
Time taken for the probe to reach the front of the rocket, t' = 1.11 × 10^–6 s

Step 2: Analyse the situation

In reference to an observer at rest on the ground, they will see the probe taking longer to reach the front of the ship
Since object in question, the probe, is moving in both reference frames, we need to use a Lorentz transformation

Step 3: Calculate the gamma factor

$γ = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} = \frac{1}{\sqrt{1 - \frac{{(0.91 c)}^{2}}{c^{2}}}}$

$γ = \frac{1}{\sqrt{1 - 0 . 91^{2}}} = 2.412$

Step 4: Substitute values into the Lorentz transformation

Since the observer is at rest, the Lorentz equation for time t must be used

$t = γ (t' + \frac{v x'}{c^{2}})$

$t = 2.412 ((1.11 \times 10^{- 6}) + \frac{(0.91 c) (150)}{c^{2}}) = 2.412 ((1.11 \times 10^{- 6}) + \frac{(0.91) (150)}{3 \times 10^{8}})$

$t = 3.8 \times 10^{- 6} s$

Examiner Tips and Tricks

Always check that your value of $γ$ is greater than 1.

You will often be given a speed v in terms of c e.g. v = 0.90c etc. When you put this value into the gamma factor, this is squared. Therefore, you do not need to put in 3.0 × 10⁸ at all into your calculator, as the c² will cancel.

E.g. $γ = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} = \frac{1}{\sqrt{1 - \frac{{(0.90 c)}^{2}}{c^{2}}}} = \frac{1}{\sqrt{1 - \frac{{(0.90)}^{2} {(c)}^{2}}{c^{2}}}}$

$γ = \frac{1}{\sqrt{1 - \frac{{(0.90)}^{2} {(c)}^{2}}{c^{2}}}} = \frac{1}{\sqrt{1 - {(0.90)}^{2}}}$

The equations for x', t' and $γ$ are given in your data booklet, but you must remember the sign change if you want to calculate x or t (from the rest frame) instead!

Some textbooks may go further into this for your understanding, you will not be expected to derive these equations in your exam. You will only be assessed on how to use them.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent

Lorentz Transformations (DP IB Physics: HL): Revision Note

Lorentz Transformation Equations

The Lorentz Factor

Lorentz Transformation Equations

Galilean vs. Lorentz Transformations

Lorentz (v ≈ c)

Galilean (v << c)

$x' = γ (x - v t)$

$x' = x - v t$

$x = γ (x' + v t')$

$x = x' + v t$

$t' = γ (t - \frac{v x}{c^{2}})$

$t' = t$

$t = γ (t' + \frac{v x'}{c^{2}})$

$t = t'$

$y = y'$

$y = y'$

$z = z'$

$z = z'$

Worked Example

Examiner Tips and Tricks

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Ashika

Reviewer: Caroline Carroll

Lorentz Transformations (DP IB Physics: HL): Revision Note

Lorentz Transformation Equations

The Lorentz Factor

Lorentz Transformation Equations

Galilean vs. Lorentz Transformations

Lorentz (v ≈ c)

Galilean (v << c)

x' = γ(x − vt)

x' = x − vt

x = γ(x' + vt')

x = x' + vt

t' = γ(t − vx c2)

t' = t

t = γ(t' + vx' c2)

t = t'

y = y'

y = y'

z = z'

z = z'

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Ashika

Reviewer: Caroline Carroll

$x' = γ (x - v t)$

$x' = x - v t$

$x = γ (x' + v t')$

$x = x' + v t$

$t' = γ (t - \frac{v x}{c^{2}})$

$t' = t$

$t = γ (t' + \frac{v x'}{c^{2}})$

$t = t'$

$y = y'$

$y = y'$

$z = z'$

$z = z'$