Impulse & Momentum (DP IB Physics) : Revision Note
Impulse & Momentum
When an external resultant force acts on an object for a very short time and changes the object's motion, we call this impulse
For example:
Kicking a ball
Catching a ball
A collision between two objects
Impulse is the product of the force applied and the time for which it acts
Where:
= impulse, measured in newton seconds (N s)
= resultant external force applied, measured in newtons (N)
= change in time over which the force acts, measured in seconds (s)
Because the force is acting for only a short time, it is very difficult to directly measure the magnitude of the force or the time for which it acts
Instead, it can be measured indirectly
Newtons' second law can be stated in terms of momentum
The resultant force on an object is equal to its rate of change of momentum
Therefore:
Where:
= resultant force, measured in newtons (N)
= change in momentum, measured in kilogram metres per second (kg m s−1)
= change in time over which the force acts, measured in seconds (s)
Change in momentum is equal to impulse
Therefore, change in momentum can be used to measure impulse indirectly
Where:
= impulse, measured in newton seconds (N s)
= change in momentum, measured in kilogram metres per second (kg m s−1)
= mass, measured in kilograms (kg)
= final velocity, measured in meters per second (m s−1)
= initial velocity, measured in meters per second (m s−1)
These equations are only used when the force F is constant
Impulse, like force and momentum, is a vector quantity with both a magnitude and direction
The impulse is always in the direction of the resultant force
A small force acting over a long time has the same effect as a large force acting over a short time
Examiner Tips and Tricks
If you follow the units in your calculations (which is always a good idea!), the base units for the newton are:
1 N = 1 kg m s−2
This is why FΔt = Δp
kg m s−2 × s = kg m s−1
Impulse Examples
When rain and hail (frozen water droplets) hit an umbrella they feel very different. This is an example of impulse.
Water droplets tend to splatter and roll off the umbrella because there is only a very small change in momentum
Hailstones have a larger mass and tend to bounce back off the umbrella, because there is a greater change in momentum
Therefore, the impulse that the umbrella applies on the hail stones is greater than the impulse the umbrella applies on the raindrops
This means that more force is required to hold an umbrella upright in hail compared to rain
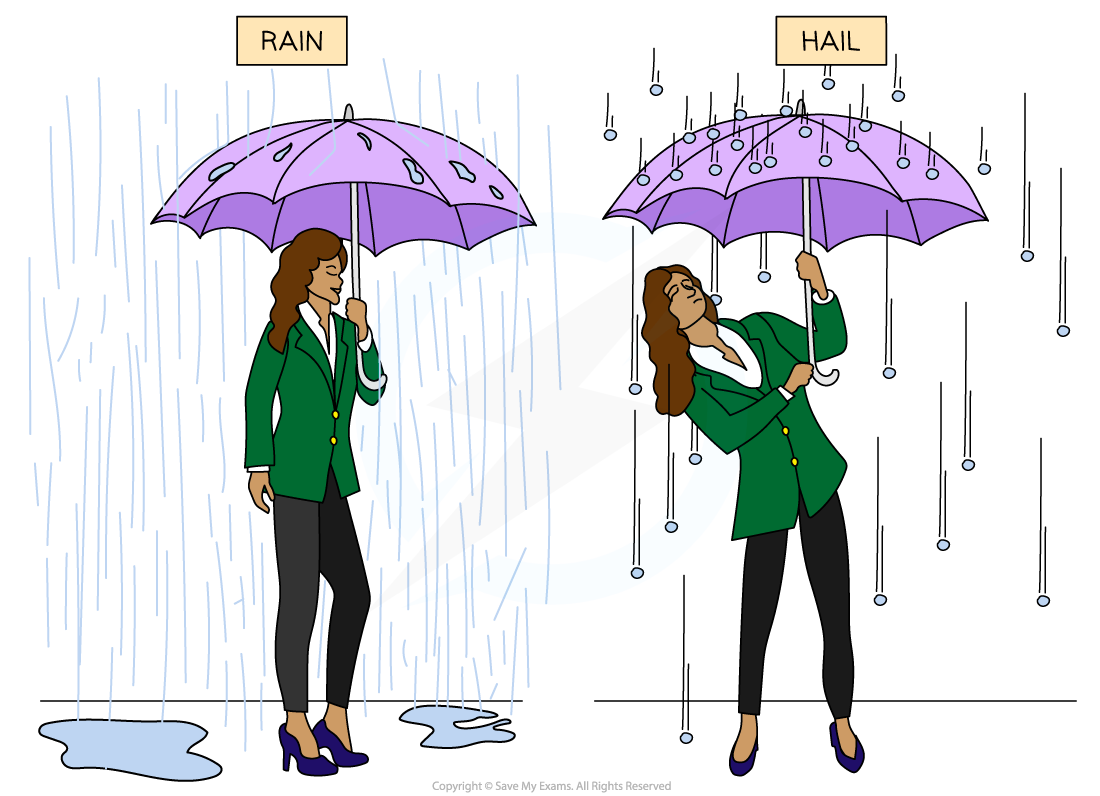
The impulse applied by the umbrella to the hail stones is greater than the impulse applied to the rain drops
The concept of impulse is used to prevent injury
Increasing the time over which the change in momentum occurs, reduces the force experienced by the person
For example, in cricket:
A cricket ball travels at very high speeds and therefore has a high momentum
When a fielder catches the ball, the ball exerts a force on their hands
Stopping a ball with high momentum abruptly will exert a large force on their hands
This is because the change in momentum (impulse) acts over a short period of time which creates a large force on the fielder's hands and could cause serious injury
A fielder moves their hands back when they catch the ball, which increases the time for the change in momentum to occur
This means there will be less force exerted on the fielder's hands and therefore, less chance of injury
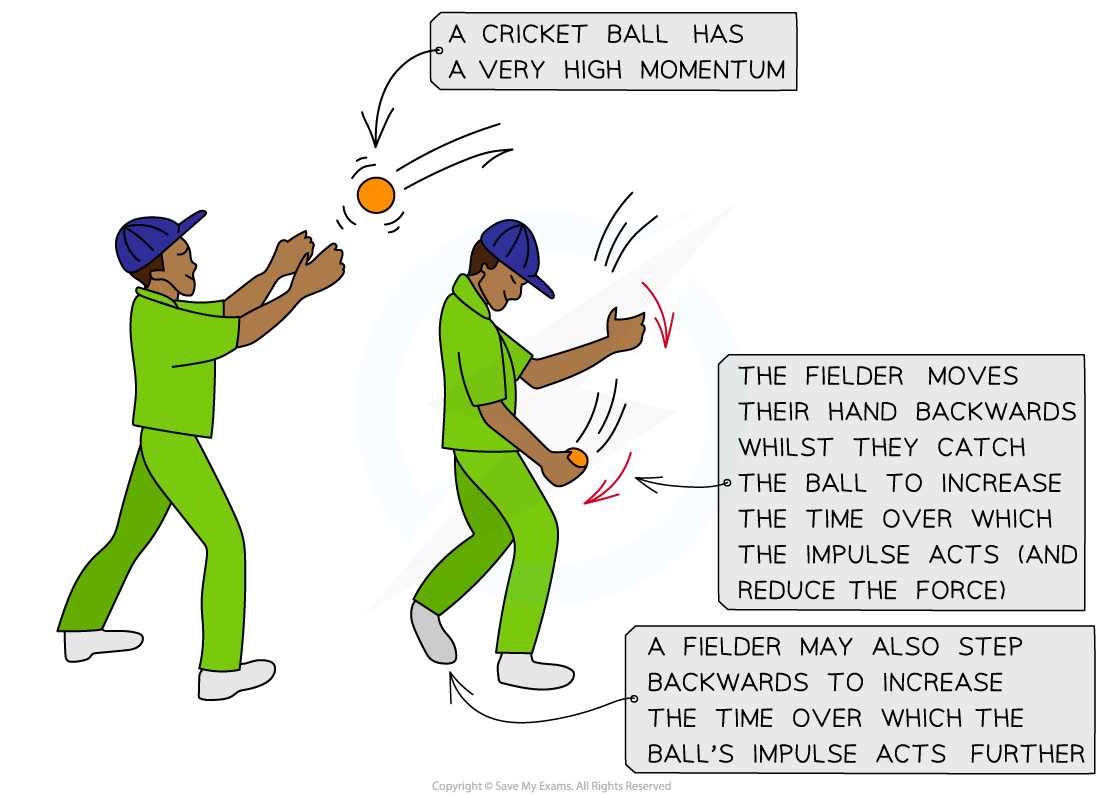
A cricket fielder moves their hands backwards when catching a cricket ball to reduce the force it will exert on their hands
Worked Example
A 58 g tennis ball moving horizontally to the left at a speed of 30 m s–1 is struck by a tennis racket which returns the ball to the right at 20 m s–1.
(a) Calculate the impulse of the racket on the ball
(b) State the direction of the impulse
Answer:
(a)
Step 1: List the known quantities
Taking the direction of the initial motion of the ball as positive (the left)
Initial velocity, u = 30 m s–1
Final velocity, v = –20 m s–1
Mass, m = 58 g = 58 × 10–3 kg
Step 2: Write down the impulse equation
Step 3: Substitute in the known values
(b)
Step 1: State the direction of the impulse
Since the impulse is negative, it must be in the opposite direction to which the tennis ball was initially travelling
Therefore, (since the left is taken as positive) the direction of the impulse is to the right
Examiner Tips and Tricks
Remember that if an object changes direction, then this must be reflected by the change in the sign of the velocity (and impulse). This is the most common mistake made by students. Velocity, impulse, force and momentum are all vectors!
For example, if the left is taken as positive and therefore the right as negative, an impulse of 20 N s to the right is equal to −20 N s

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
