Angular Velocity (DP IB Physics)

Angular Velocity

Motion in a Straight Line

• When an object moves in a straight line at a constant speed its motion can be described as follows:

  • The object moves at a constant velocity, v

  • Constant velocity means zero acceleration, a

  • Newton's First Law of motion says the object will continue to travel in a straight line at a constant speed unless acted on by another force

  • Newton's Second Law of motion says that for zero acceleration there is no net or resultant force

• For example, an ice hockey puck moving across a flat frictionless ice rink

An ice puck moving in a straight line

Motion in a Circle

• If one end of a string was attached to the puck, and the other attached to a fixed point, it would no longer travel in a straight line, it would begin to travel in a circle

The red arrows represent the velocity vectors of the puck. If the string were cut, the puck would move off in the direction shown by the red vector, as predicted by Newton’s first law.

• The motion of the puck can now be described as follows:

  • As the puck moves it stretches the string a little to a length r

  • The stretched string applies a force to the puck pulling it so that it moves in a circle of radius r around the fixed point

• The force acts at 90° to the velocity so there is no force component in the direction of velocity

  • As a result, the magnitude of the velocity is constant

  • However, the direction of the velocity changes

• As it starts to move in a circle the tension of the string continues to pull the puck at 90° to the velocity

  • The speed does not change, hence, this is called uniform circular motion

The applied force (tension) from the string causes the puck to move with uniform circular motion

Time Period & Frequency

• If the circle has a radius r, then the distance through which the puck moves as it completes one rotation is equal to the circumference of the circle = 2πr

• The speed of the puck is therefore equal to:

• Where:

  • r = the radius of the circle (m)

  • T = the time period (s)

• This is the same as the time period in waves and simple harmonic motion (SHM)

• The frequency, f, can be determined from the equation:

• Where:

  • f = frequency (Hz)

  • T = the time period (s)

Angles in Radians

• A radian (rad) is defined as:

  The angle subtended at the centre of a circle by an arc equal in length to the radius of the circle

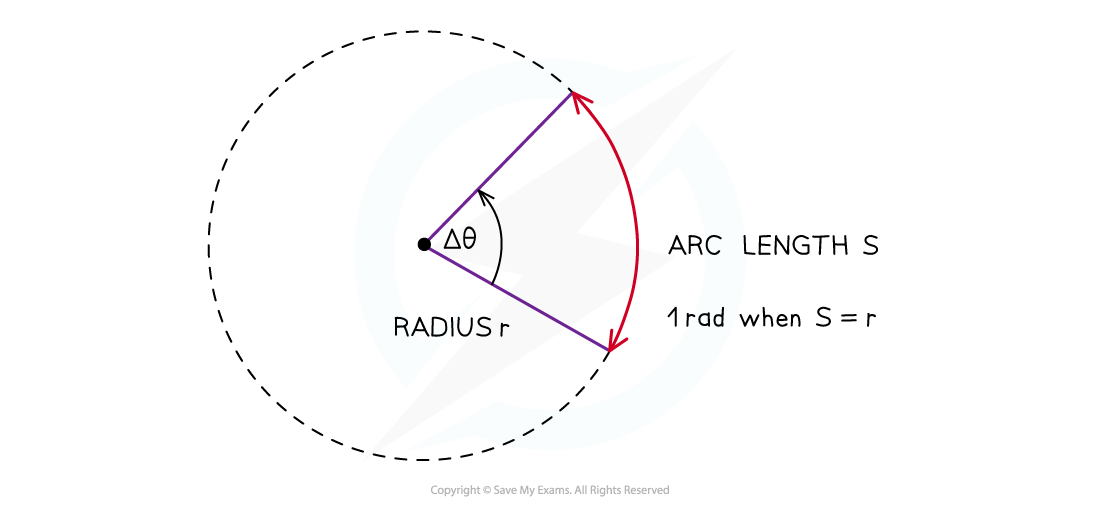
When the angle is equal to one radian, the length of the arc (S) is equal to the radius (r) of the circle

• Radians are commonly written in terms of π

• The angle in radians for a complete circle (360°) is equal to: 

• Use the following equation to convert from degrees to radians:

• Use the following equation to convert from radians to degrees:

Table of common degrees to radians conversions

Angular Displacement

• In circular motion, it is more convenient to measure angular displacement in units of radians rather than units of degrees

• Angular displacement is defined as:

  The change in angle, in radians, of a body as it rotates around a circle

• Where:

  • Δθ = angular displacement, or angle of rotation (radians)

  • S = length of the arc, or the distance travelled around the circle (m)

  • r = radius of the circle (m)

An angle in radians, subtended at the centre of a circle, is the arc length divided by the radius of the circle

Angular Speed

• Any object rotating with a uniform circular motion has a constant speed but constantly changing velocity

• Its velocity is changing so it is accelerating

  • But at the same time, it is moving at a constant speed

• The angular speed, ⍵, of a body in circular motion is defined as:

  The change in angular displacement with respect to time

• Angular speed is a scalar quantity and is measured in rad s^–1

• The angular speed does not depend on the length of the line AB

• The line AB will sweep out an angle of 2π rad in a time T

The angular speed is ω is the rate at which the line AB rotates

Angular Velocity & Linear Speed

• Angular velocity is a vector quantity and is measured in rad s^–1

• Angular speed is the magnitude of the angular velocity

• Although the angular speed doesn’t depend on the radius of the circle, the linear speed does

The angle Δθ is swept out in a time Δt, but the arc lengths s and S are different and so are the linear speeds

• The linear speed, v, is related to the angular speed, ⍵, by the equation:

• Where:

  • v = linear speed (m s^–1)

  • r = radius of circle (m)

  • ⍵ = angular speed (rad s^–1)

• Taking the angular displacement of a complete cycle as 2π, the angular speed ⍵ can be calculated using the equation:

• Therefore, the linear velocity can also be written as: