The Bohr Model of Hydrogen (DP IB Physics) : Revision Note
The Bohr Model of Hydrogen
Hydrogen is the simplest atom in existence, making it ideal for experiments investigating the nature of electron energy levels
Line spectra produced by hydrogen atoms showed that
Electrons are able to jump, or transition, between specific energy levels producing specific energy photons
Different transitions can be categorised into series, or families, of lines
The Lyman series converges on the ground state (n = 1) for electrons
The Balmer series converges on the second energy level (n = 2)
The Ritz-Paschen converges on the third energy level (n = 3) and so on

The transitions observed in hydrogen line spectra can be classed into series
The Lyman series photons will have the highest energies since they have the shortest wavelength
These transitions tend to produce ultraviolet photons
The Pfund series photons will have the lowest energies since they have the longest wavelength
These transitions tend to produce infrared photons

Representing the electron jumps in the hydrogen spectra
The finding of these electron transitions helped scientists to understand how electrons work to produce photons of specific wavelength and energy
This led to the development of the Bohr model of hydrogen, which states that
Electrons can only move in fixed orbits
The orbital radius of electrons is restricted to certain values
The discrete energy of the transitions in the Bohr model for hydrogen are described by the equation:
Where
E = photon energy (J)
n = an integer 1, 2, 3 etc. to describe the energy level of an atom
Worked Example
Determine the frequency of an emitted photon from a hydrogen atom when an electron makes a transition between levels n = 4 and n = 2.
Answer:
Step 1: List the known quantities
Transition between n = 4 and n = 2
Planck’s constant, h = 6.63 × 10–34 J s
Electronvolt, eV = 1.6 × 10–19 J
Step 2: Determine an equation for the change in energy ΔE
Step 3: Calculate the change in energy, in eV, for the photon using the given equation
Step 4: Rearrange the photon energy equation for frequency f
Step 5: Substitute the known values into the equation for frequency
Quantisation of Angular Momentum
Angular momentum is a property of any spinning or rotating body, very similar to linear momentum
In linear motion, momentum is the product of mass and velocity
In rotational motion, the momentum is the product of moment of inertia and angular speed
Angular momentum is a vector, which means:
The magnitude is equal to the momentum of the particle times its radial distance from the centre of its circular orbit
The direction of the angular momentum vector is normal to the plane of its orbit with the direction being given by the corkscrew rule
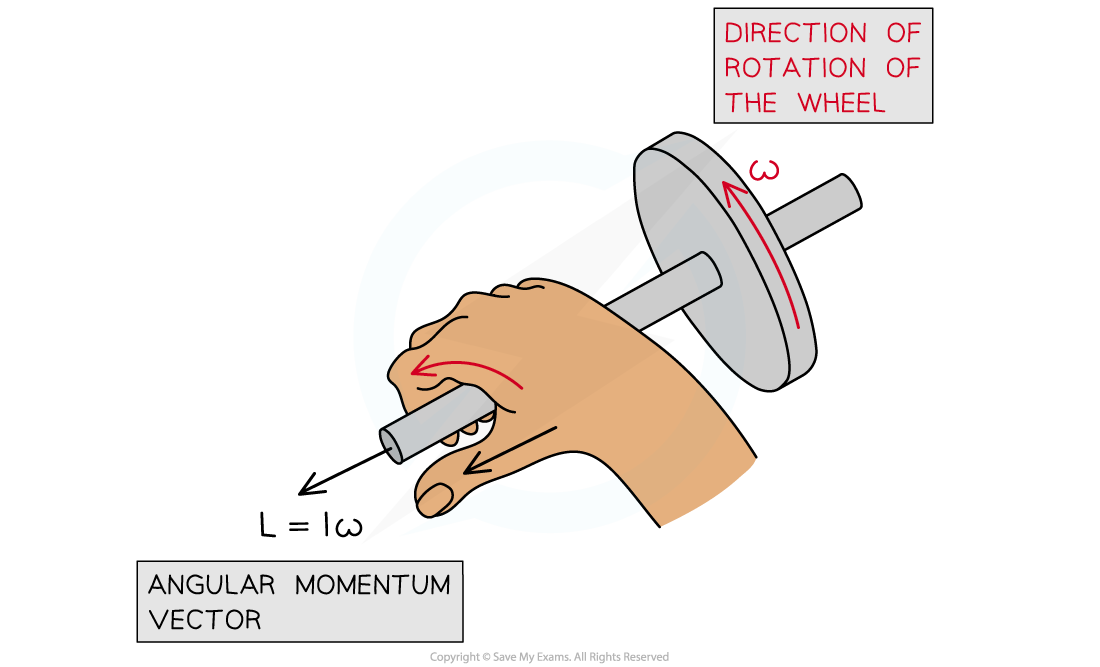
Angular momentum acts at right angles to the direction of rotation
Niels Bohr proposed that the angular momentum L of an electron in an energy level is quantised in integer multiples of Planck's constant over 2π:
Where:
n = an integer (n = 1, 2, 3...)
h = Planck’s constant
Hence the angular momentum for an electron in a circular orbit is constant
De Broglie proposed that an electron with momentum p = mv has a wavelength λ given by
For an electron moving in a straight line, the matter wave takes a familiar wave shape consisting of peaks and troughs
Although the electron itself isn't oscillating up and down, only the matter wave is

de Broglie matter wave for an electron moving in a straight line at constant speed
For the same electron moving in a circle, the matter wave still has a sinusoidal shape but is wrapped into a circle

de Broglie matter wave for an electron moving in a circular orbit at constant speed
As the electron continues to orbit in a circle two possibilities may occur:
1. On completing one oscillation, the waves overlap in phase
The waves will continue in phase over many orbits giving rise to constructive interference and a standing wave

de Broglie matter wave where n = 3. Here the circumference of the circular orbit is 3λ
2. On completing one oscillation, the waves overlap but they are not in phase
In other words, the peak of one wave does not overlap with the peak of another wave, and the trough of one wave does not overlap with the trough of another wave,
This means that where the waves overlap, destructive interference occurs and as a result, no such electron orbit is allowed

de Broglie matter wave where 3λ is less than the orbit's circumference
Hence, the circumference of the orbit
must equal an integer number of wavelengths
for a standing wave to form:
Using the de Broglie relation:
Since momentum is equal to
:
Rearranging for angular momentum
:
This is known as the Bohr Condition
Where:
n = integer number of energy level
h = Planck's constant (J s)
m = mass of an electron (kg)
v = velocity of electron (m s–1)
r = radius of orbit (m)
Worked Example
Determine the velocity of the electron in the first Bohr orbit of the hydrogen atom.
You may use the following values:
Mass of an electron = 9.1 × 10−31 kg
Radius of the orbit = 0.529 × 10−10 m
Planck's constant = 6.63 × 10−34 kg m2 s−1
Answer:
Step 1: List the known quantities
First orbital level, n = 1
Mass of an electron, m = 9.1 × 10−31 kg
Radius of the orbit, r = 0.529 × 10−10 m
Planck's constant, h = 6.63 × 10−34 kg m2 s-1
Step 2: Write the Bohr Condition equation and rearrange for velocity, v
Step 3: Substitute the values in and calculate the velocity v
Step 4: Write the final answer
Velocity of an electron (n = 1): v = 2.2 × 106 m s−1

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
