Rutherford Scattering & Nuclear Radius (DP IB Physics) : Revision Note
Nuclear Radius
The radius of a nucleus depends on the nucleon number A of the atom
The greater the number of nucleons a nucleus has, the greater the space the nucleus occupies, hence giving it a larger radius
The exact relationship between the radius and nucleon number can be determined from experimental data, such as Rutherford scattering
By doing this, physicists were able to deduce the following relationship:
Where:
R = nuclear radius (m)
A = nucleon / mass number
R0 = Fermi radius
The constant of proportionality R0 = 1.20 × 10−15 m is known as the Fermi radius
This is the radius of a hydrogen nucleus which contains only one proton (A = 1)
Nuclear Density
Assuming that the nucleus is spherical, its volume is equal to:
Combining this with the expression for nuclear radius gives:
This tells us that the nuclear volume V is proportional to the mass of the nucleus m, which is equal to
Where u = atomic mass unit (kg)
Using the definition for density, nuclear density is equal to:
Since the mass number A cancels out, the remaining quantities in the equation are all constants
Therefore, this shows the density of the nucleus is:
The same for all nuclei
Independent of the radius
The fact that nuclear density is constant shows that nucleons are evenly separated throughout the nucleus regardless of their size
The accuracy of nuclear density depends on the accuracy of the constant R0
As a guide, nuclear density should always be of the order 1017 kg m–3
Nuclear density is significantly larger than atomic density which suggests:
The majority of the atom’s mass is contained in the nucleus
The nucleus is very small compared to the atom
Atoms must be predominantly empty space
Worked Example
Determine the value of nuclear density.
You may take the constant of proportionality R0 to be 1.20 fm.
Answer:
Step 1: Derive an expression for nuclear density
Using the equation derived above, the density of the nucleus is:
Step 2: List the known quantities
Atomic mass unit, u = 1.661 × 10–27 kg
Constant of proportionality, R0 = 1.20 fm = 1.20 × 10–15 m
Step 3: Substitute the values to determine the nuclear density
Examiner Tips and Tricks
You do not need to remember the value of the Fermi radius R0 as it is included in the data booklet in the 'fundamental constants' section.
Rutherford Scattering Experiment
In the Rutherford scattering experiment, alpha particles are fired at a thin gold foil
Initially, before interacting with the foil, the particles have kinetic energy equal to
Some of the alpha particles are found to come straight back from the gold foil
This indicates that there is electrostatic repulsion between the alpha particles and the gold nucleus
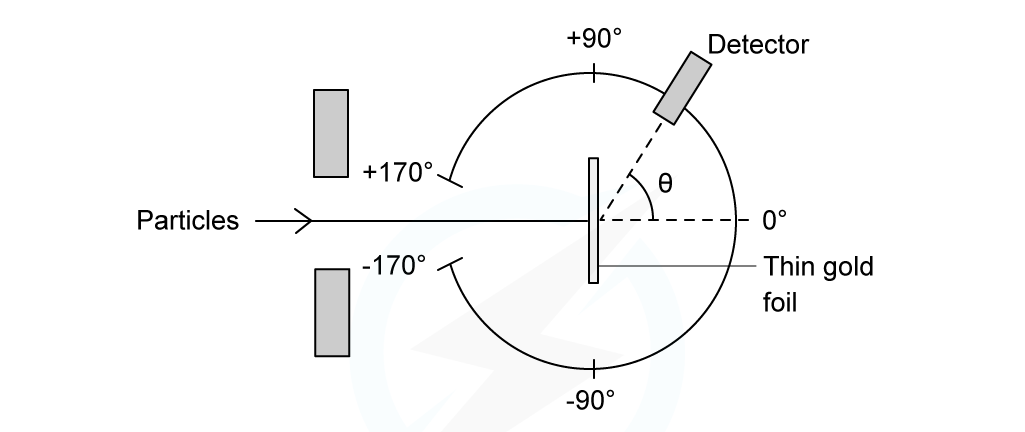
Experimental set-up of the Rutherford alpha scattering experiment
At the point of closest approach d, the repulsive force reduces the speed of the alpha particles to zero momentarily, before any change in direction
At this point, the initial kinetic energy
of the alpha particle is equal to the electric potential energy
of the target nucleus:
Where the electric potential energy is given by
Where:
Charge of an alpha particle, Q = 2e
Charge of a target nucleus, q = Ze
Z = proton (atomic) number
e = elementary charge (C)
k = Coulomb constant
This gives an expression for the potential energy at the point of repulsion:
Which, due to the conservation of energy also gives the initial kinetic energy possessed by the alpha particle
Rearranging for the distance of closest approach d
This gives a value for the radius of the nucleus, assuming the alpha particle is fired at a high energy

The closest approach method of determining the size of a gold nucleus
Examiner Tips and Tricks
Make sure you're comfortable with the calculations involved with the alpha particle closest approach method, as this is a common exam question.
You will be expected to remember that the charge of an α is the charge of 2 protons (2 × the charge of an electron)

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?