Nuclear Energy Levels (DP IB Physics) : Revision Note
Nuclear Energy Levels
A nucleus can exist in an excited state in the same way as an electron
Once an unstable nucleus has decayed, it may emit any remaining energy in the form of a gamma photon (γ)
The emission of a γ photon does not change the number of protons or neutrons in the nucleus, it only allows the nucleus to lose energy
This happens when a daughter nucleus is in an excited state after a decay
This excited state is usually very short-lived, and the nucleus quickly moves to its ground state, either directly or via one or more lower-energy excited states
Metastable technetium-99m is a technetium-99 nucleus in an excited energy state
One common application of this is the use of technetium-99m as a γ source in medical diagnosis
The ‘m’ stands for metastable which means the nucleus exists in a particularly stable excited state
Technetium-99m is the decay product of molybdenum-99, which can be found as a product in nuclear reactors
The decay of molybdenum-99 is shown below:
Nuclear energy levels are similar to electron energy levels
The nuclear energy level diagram of molybdenum-99 can be represented as follows:

A diagonal line represents the decay mode (usually alpha or beta)
The excited state, or states, are generally stacked in descending energy order to the right of the decay
Worked Example
A nucleus of iron Fe-59 decays into a stable nucleus of cobalt Co-59. It decays by β– emission followed by the emission of γ-radiation as the Co-59 nucleus de-excites into its ground state.
The total energy released when the Fe-59 nucleus decays is 2.52 × 10–13 J. The Fe-59 nucleus can decay to one of three excited states of the cobalt-59 nucleus as shown below. The energies of the excited states are shown relative to the ground state.

Following the production of excited states of Co-59, γ-radiation of discrete wavelengths is emitted.
(a) Calculate the maximum possible kinetic energy of the β– particle emitted in MeV
(b) State the maximum number of discrete wavelengths that could be emitted
(c) Calculate the longest wavelength of the emitted γ-radiation
Answer:
Part (a)
Step 1: Identify the beta emission with the largest energy gap

Step 2: Calculate the energy difference
ΔE = (2.52 – 1.76) × 10–13 = 7.6 × 10–14 J
Step 3: Convert from J to MeV
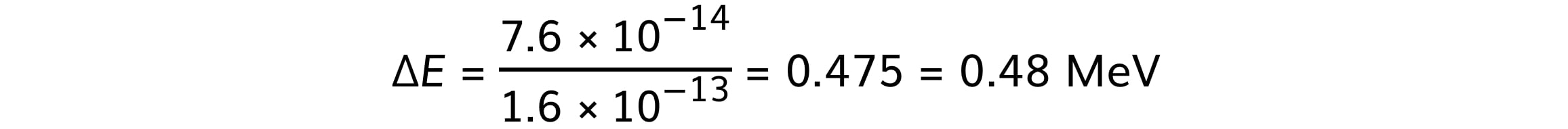
1 MeV = 1.6 × 10–13 J
Part (b)

There are 6 possible transitions, hence 6 discrete wavelengths could be emitted
Part (c)
Step 1: Identify the emission with the longest wavelength / smallest energy gap

Longest wavelength = lowest frequency = smallest energy
Step 2: Calculate the energy difference
ΔE = (2.29 – 2.06) × 10–13 = 2.3 × 10–14 J
Step 3: Relate photon energy and wavelength
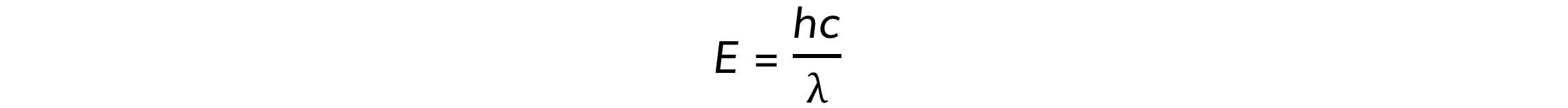
Where:
h = Planck’s constant
c = speed of light
Step 4: Calculate the wavelength associated with the energy change
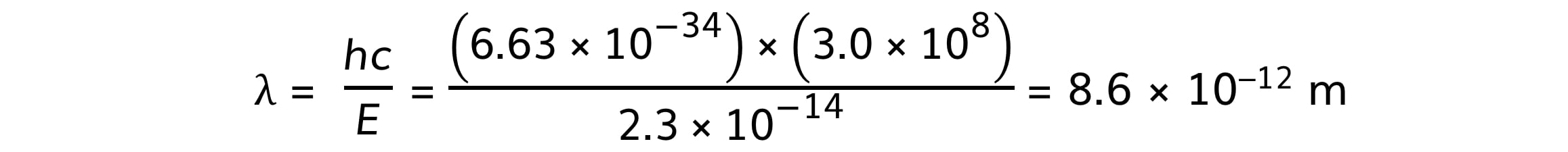

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
