Revision NotesExam QuestionsFlashcardsPast Papers
IBPhysicsDPHLRevision NotesNuclear & Quantum PhysicsQuantum PhysicsThe Photoelectric Equation

The Photoelectric Equation (DP IB Physics)

Revision Note

Katie M

Author

Katie M

Last updated

The Photoelectric Equation

  • The energy of a photon is equal to:

E space equals space h f

  • This equation shows that:

    • Photon energy open parentheses E close parentheses and frequency open parentheses f close parentheses are directly proportional

    • Therefore, a photon which has a greater frequency than the threshold frequency of the metal will also have a greater energy than the work function of the metal

  • When a photon is incident on the surface of a metal, its energy is divided as follows:

    • The energy equal to the work function is used to liberate a photoelectron from the metal

    • The remaining energy will be transferred to the photoelectron as kinetic energy

  • This can be described using the photoelectric equation:

h f space equals space ϕ space plus space E subscript k space m a x end subscript

  • The maximum kinetic energy a photoelectron can have is therefore:

E subscript k space m a x end subscript space equals space h f space minus space ϕ

  • Where:

    • h = Planck's constant (J s)

    • f = frequency of the incident radiation (Hz)

    • capital phi = work function of the metal (J) 

    • E subscript K space m a x end subscript = maximum kinetic energy of a photoelectron (J)

  • The photoelectric equation shows that incident photons:

    • Which do not have enough energy to overcome the work function (Φ) will not liberate any photoelectrons

    • Which have a frequency equal to the threshold frequency open parentheses f subscript 0 close parentheses will be just able to liberate photoelectrons from the surface of the metal

    • These photons have energy equal to: 

E space equals space h f subscript 0 space equals space capital phi

  • The photoelectric equation shows that for photoelectrons: 

    • Those that are just able to escape the surface of the metal will have zero kinetic energy

    • The majority will have kinetic energies less than E subscript k space m a x end subscript

    • The maximum kinetic energy E subscript k space m a x end subscript depends only on the frequency of the incident photon and not the intensity of the radiation

Graphical Representation of Work Function

  • The photoelectric equation can be rearranged into the equation of a straight-line:

y space equals space m x space plus space c

  • Comparing this to the photoelectric equation:

E subscript K space m a x end subscript space equals space h f space minus space capital phi

  •  A graph of maximum kinetic energy E subscript K space m a x end subscript against frequency f can be obtained

  • The key elements of the graph are:

    • The work function Φ is the y-intercept

    • The threshold frequency f0 is the x-intercept

    • The gradient is equal to Planck's constant h

    • There are no electrons emitted below the threshold frequency f0

Worked Example

The graph below shows how the maximum kinetic energy Ek of electrons emitted from the surface of sodium metal varies with the frequency f of the incident radiation.

5-2-2-work-function-graph-worked-example

Calculate the work function of sodium in eV.

Answer:

Step 1: Write out the photoelectric equation and rearrange it to fit the equation of a straight line

h f space equals space capital phi space plus space E subscript K space m a x end subscript

E subscript K space m a x end subscript space equals space h f space minus space capital phi

y space equals space m x space plus space c

  • Therefore, when E subscript K space equals space 0, h f space equals space capital phi and f space equals space f subscript 0

 Step 2: Identify the threshold frequency from the x-axis of the graph

  • From the graph:

    • When E subscript K space equals space 0, threshold frequency:  f space equals space f subscript 0 = 4 × 1014 Hz

Step 3: Calculate the work function

capital phi space equals space h f subscript 0 space equals space open parentheses 6.63 cross times 10 to the power of negative 34 end exponent close parentheses space cross times space open parentheses 4 cross times 10 to the power of 14 close parentheses

Work function:  capital phi = 2.652 × 10−19 J

Step 4: Convert the work function into eV

  • To convert from J to eV:  divide by 1.6 × 10−19 J

E space equals space fraction numerator 2.652 space cross times space 10 to the power of negative 19 end exponent over denominator 1.6 space cross times space 10 to the power of negative 19 end exponent end fraction = 1.66 eV

Examiner Tips and Tricks

When using the photoelectric equation, hf, Φ and Ek(max) must all have the same units, so make sure your quantities are all in either eV or J.

Remember that the maximum kinetic energy part of the photoelectric equation is for a photoelectron and not a photon!

If the photoelectron is emitted with the maximum kinetic energy E subscript k space m a x end subscript, it will be travelling at its maximum velocity v subscript m a x end subscript, which can be calculated using the kinetic energy equation:

E subscript k space m a x end subscript space equals space 1 half m subscript e v subscript m a x end subscript squared

Intensity & Photoelectric Current

Kinetic Energy & Intensity

  • The kinetic energy of the photoelectrons is independent of the intensity of the incident radiation

    • This is because each electron can only absorb one photon

    • Kinetic energy is only dependent on the frequency of the incident radiation

  • Intensity is the rate of energy transferred per unit area and is related to the number of incident photons striking the metal plate

  • Increasing the number of photons striking the metal plate will not increase the kinetic energy of the photoelectrons; it will increase the number of photoelectrons emitted

Why Kinetic Energy is a Maximum

  • Each electron in the metal acquires the same amount of energy from the photons in the incident monochromatic radiation.

  • However, the energy required to remove an electron from the metal varies because some electrons are on the surface whilst others are deeper in the metal

    • The photoelectrons with the maximum kinetic energy will be those on the surface of the metal since they do not require as much energy to leave the metal

    • The photoelectrons with lower kinetic energy are those deeper within the metal since some of the energy absorbed from the photon is used to approach the metal surface (and overcome the work function)

    • There is less kinetic energy available for these photoelectrons once they have left the metal

Photoelectric Current

  • The photoelectric current is a measure of the number of photoelectrons emitted per second

    • The value of the photoelectric current is calculated by the number of electrons emitted multiplied by the charge on one electron

  • Photoelectric current is proportional to the intensity of the radiation incident on the surface of the metal

  • This is because intensity is proportional to the number of photons striking the metal per second

  • Since each photoelectron absorbs a single photon, the photoelectric current must be proportional to the intensity of the incident radiation

2-4-3-ke-photocurrent-graphs

Sketch graphs showing the trends in the variation of electron kinetic energy with the frequency and intensity of the incident light and the variation of photocurrent with the intensity of the incident light

Examiner Tips and Tricks

It is a common misconception that photoelectric current is independent of photon frequency. In an exam question, you could be asked about the effect on photoelectric current by:

  • Changing the intensity of the incident radiation whilst keeping the frequency constant

  • Changing the frequency of the incident radiation whilst keeping the intensity constant

In both scenarios, the photoelectric current will change

If you change the frequency of the incident light whilst keeping the number of photons emitted by the light source constant, then the photoelectric current will not change. This is because changing the frequency will change the energy of the emitted photons, but the number of photons will remain the same.

However, if you change the frequency of the incident light whilst keeping the intensity constant, the photoelectric current will change. This is because intensity is power per unit area which is equal to the rate of energy transfer per unit area

I space equals space fraction numerator space P over denominator A end fraction space equals space fraction numerator space E over denominator t A end fraction

The energy transferred comes from the photons, where the energy of a single photon is hf

I space equals space fraction numerator space h f over denominator t A end fraction

So, to account for n number of photons:

I space equals space fraction numerator space n h f over denominator t A end fraction

If the frequency f is increased and the intensity I remains constant, then the number of photons n must decrease. Planck's constant h, and the area A of the metal plate do not change

This is because at higher frequencies, each photon has a higher energy, so fewer photons are required to maintain the same intensity.

Stopping Potential

  • Stopping potential V subscript S is defined as:

    The potential difference required to stop photoelectron emission from occurring

  • The photons arriving at the metal plate cause photoelectrons to be emitted

    • This is called the emitter plate

  • The electrons that cross the gap are collected at the other metal plate

    • This is called the collector plate

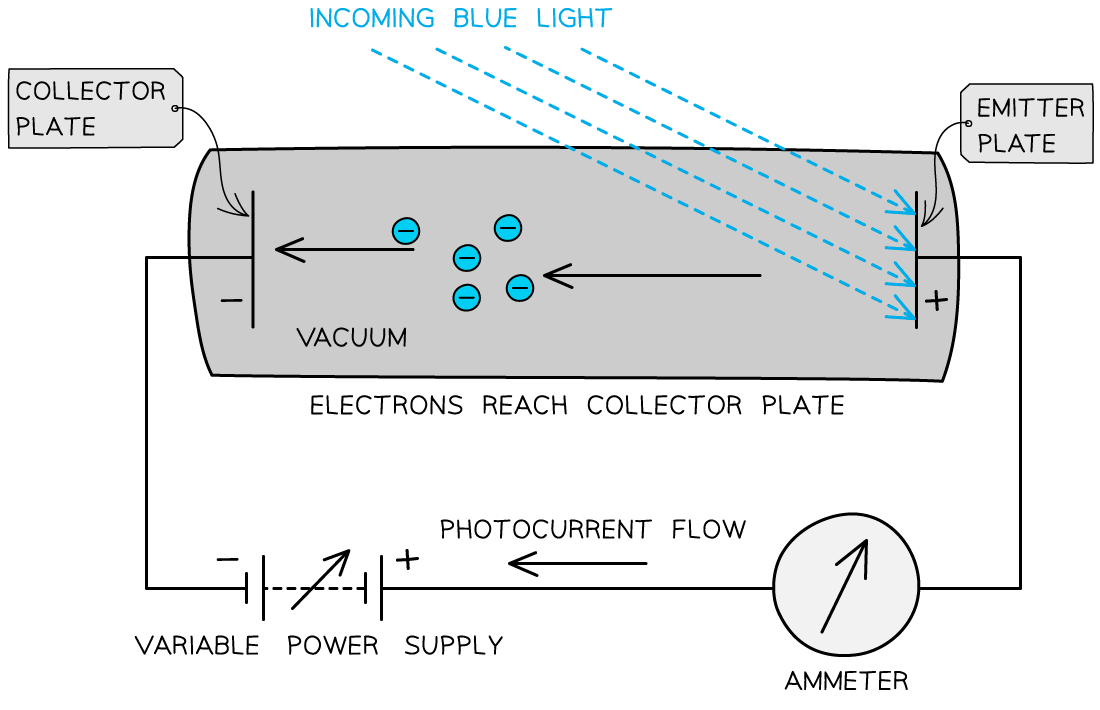
Stopping Potential, downloadable AS & A Level Physics revision notes

This setup can be used to determine the maximum kinetic energy of the emitted photoelectrons

  • The flow of electrons across the gap sets up an e.m.f. between the plates that allows a current to flow around the rest of the circuit

    • Effectively, it becomes a photoelectric cell which produces a photoelectric current

  • If the e.m.f. of the variable power supply is initially zero, the circuit operates only on the photoelectric current

  • As the supply is turned up, the emitter plate becomes more positive

    • This is because it is connected to the positive terminal of the supply

  • As a result, electrons leaving the emitter plate are attracted back towards it

    • This is because the p.d. across the tube opposes the motion of the electrons between the plates

  • If any electrons escape with high enough kinetic energy, they can overcome this attraction and cross to the collector plate

    • And if they don't have enough energy, they can't cross the gap

  • By increasing the e.m.f. of the supply, eventually, a p.d. will be reached at which no electrons will be able to cross the gap

    • This value of e.m.f. is equal to the stopping potential V subscript S

  • At this point, the energy needed to cross the gap is equal to the maximum kinetic energy E subscript K space m a x end subscript of the electrons

V subscript s space equals fraction numerator space W over denominator Q end fraction space equals fraction numerator space E over denominator Q end fraction space equals fraction numerator space E subscript k space m a x end subscript over denominator e end fraction

  • Therefore:

E subscript K space m a x end subscript space equals space e V subscript S

  • Where:

    • E subscript K space m a x end subscript = maximum kinetic energy of the electrons (J)

    • e = elementary charge (C)

    • V subscript S = stopping voltage (V)

Intensity and Stopping Potential

  • Increasing the intensity of the incident radiation on the plate increases

    • The number of photons incident on the metal plate

    • The number of photoelectrons emitted from the plate, i.e. the photoelectric current

  • For a given potential difference, increasing the intensity increases the photoelectric current but the stopping potential remains the same

    • This shows that the intensity does not affect the kinetic energy of the photoelectrons

  • The maximum kinetic energy of the photons (and photoelectrons) depends only on

    • The frequency (or wavelength) of the incident photons

    • The work function of the metal

  • However, if the frequency or wavelength is changed whilst keeping the intensity constant, the photoelectric current will not be constant

  • For example, increasing the frequency of the incident radiation whilst keeping the intensity constant will cause the photoelectric current to decrease. This is because: 

    • Increasing the frequency of a source means the energy of each photon increases

    • Keeping intensity the same means the energy transferred per unit area in a given time is constant

    • So, a higher frequency source must emit fewer photons per unit area in a given time than a lower frequency source (of the same intensity)

    • If there are fewer photons incident on a given area each second, the number of electrons emitted each second must decrease

2-4-stopping-potential-at-different-intensities

The stopping potential remains constant even at different intensities, which shows that intensity does not affect the kinetic energy of the photoelectrons

Worked Example

Monochromatic light of wavelength lambda subscript 1 is incident on the surface of a metal. The stopping potential for this light is V subscript 1.

When another monochromatic light of wavelength lambda subscript 2 is incident on the same surface, the stopping potential is V subscript 2.

What is the quantity fraction numerator open parentheses V subscript 2 space minus space V subscript 1 close parentheses over denominator open parentheses fraction numerator 1 space over denominator lambda subscript 2 end fraction space minus space fraction numerator 1 space over denominator lambda subscript 1 end fraction close parentheses end fraction equal to?

A. fraction numerator h over denominator 2 straight pi end fraction                 

B. h over c                 

C. fraction numerator h c over denominator e end fraction                 

D. h over e

Answer:  C

  • The photoelectric equation for light 1 is

h f subscript 1 space equals space capital phi space plus thin space E subscript K space m a x open parentheses 1 close parentheses end subscript

Where E subscript K space m a x open parentheses 1 close parentheses end subscript space equals space e V subscript 1  and  E subscript 1 space equals space h f subscript 1 space equals fraction numerator h c over denominator lambda subscript 1 end fraction

  • The photoelectric equation for light 2 is

h f subscript 2 space equals space capital phi space plus thin space E subscript K space m a x open parentheses 2 close parentheses end subscript

Where E subscript K space m a x open parentheses 2 close parentheses end subscript space equals space e V subscript 2  and  E subscript 2 space equals space h f subscript 2 space equals fraction numerator h c over denominator lambda subscript 2 end fraction

  • Since the metal is the same, the work function capital phi is the same for both, so:

capital phi space equals fraction numerator h c space over denominator lambda subscript 1 end fraction minus space e V subscript 1 space equals space fraction numerator h c space over denominator lambda subscript 2 end fraction minus space e V subscript 2

  • Collecting the terms together and simplifying gives

e V subscript 2 space minus space e V subscript 1 space equals space fraction numerator h c space over denominator lambda subscript 2 end fraction space minus space fraction numerator h c space over denominator lambda subscript 1 end fraction

e open parentheses V subscript 2 space minus space V subscript 1 close parentheses space equals space h c open parentheses fraction numerator 1 space over denominator lambda subscript 2 end fraction space minus space fraction numerator 1 space over denominator lambda subscript 1 end fraction close parentheses

fraction numerator open parentheses V subscript 2 space minus space V subscript 1 close parentheses over denominator open parentheses fraction numerator 1 space over denominator lambda subscript 2 end fraction space minus space fraction numerator 1 space over denominator lambda subscript 1 end fraction close parentheses end fraction space equals space fraction numerator h c over denominator e end fraction

Examiner Tips and Tricks

It is important to note that the stopping potential actually holds a negative value, but since we use it to determine the maximum kinetic energy of the emitted electrons, its sign is not important in calculations, it's acceptable to just quote its magnitude.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:The Photoelectric EffectNext:The Particle Nature of Light
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.