The de Broglie Wavelength (DP IB Physics: HL): Revision Note

The de Broglie Wavelength

• Louis de Broglie thought that if waves can behave like particles, then perhaps particles can also behave like waves

• He proposed that electrons travel through space as waves

  • This would explain why they can exhibit wave-like behaviour such as diffraction

• De Broglie suggested that electrons must also hold wave properties, such as wavelength

  • This came to be known as the de Broglie wavelength

• However, he realised that all particles can show wave-like properties, not just electrons

  • He hypothesised that all moving particles have a matter wave associated with them

• The definition of a de Broglie wavelength is:

  The wavelength associated with a moving particle

• De Broglie suggested that the momentum p of a particle and its associated wavelength λ are related by the equation:

$\lambda =\frac{h}{p}$

• Since momentum p = mv, the de Broglie wavelength can be related to the speed of a moving particle v by the equation:

$\lambda =\frac{h}{mv}$

Kinetic Energy & de Broglie Wavelength

• Kinetic energy is defined as

$E_K=\frac{1}{2}m{v}^2$

$E_K=\frac{p^2}{2m}\Rightarrow p=\sqrt{2m{E}_K}$

• Combining this with the previous equation gives relationship between the de Broglie wavelength of a particle to its kinetic energy:

$\lambda =\frac{h}{p}=\frac{h}{\sqrt{2m{E}_K}}$

• Where:

  • λ = the de Broglie wavelength (m)

  • h = Planck’s constant (J s)

  • p = momentum of the particle (kg m s⁻¹)

  • E_K = kinetic energy of the particle (J)

  • m = mass of the particle (kg)

  • v = speed of the particle (m s⁻¹)

Evidence for the Wave Nature of Matter

• The majority of the time, and for everyday objects travelling at normal speeds, the de Broglie wavelength is far too small for any quantum effects to be observed

  • A typical electron in a metal has a de Broglie wavelength of about 10 nm

• Therefore, the quantum effects of diffraction will only be observable when the width of the aperture is of a similar size to the de Broglie wavelength

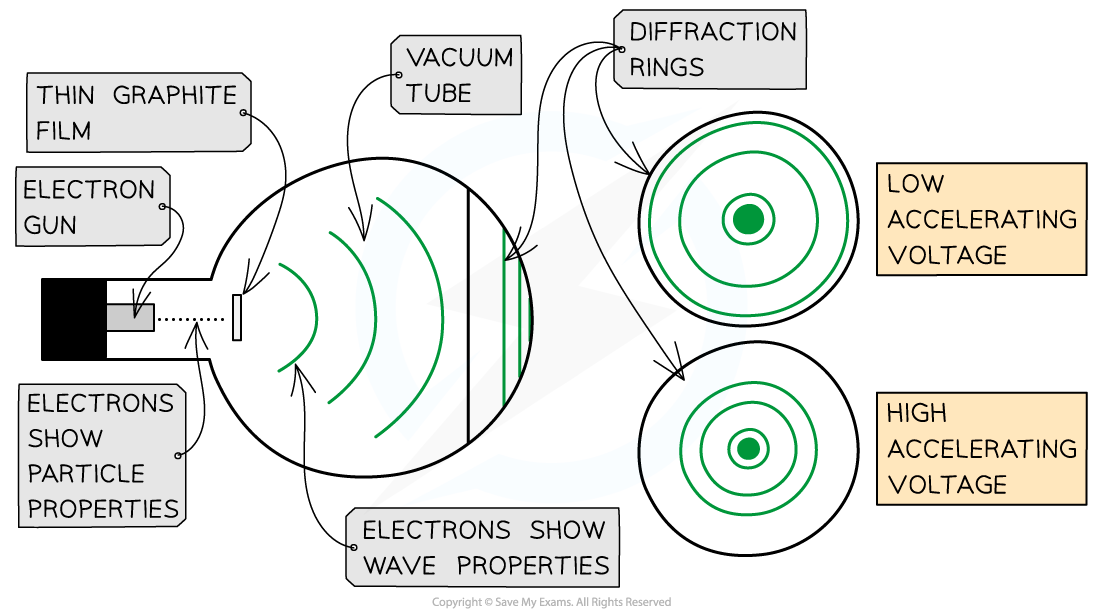
Electrons accelerated through a high potential difference demonstrate wave-particle duality 

• The electron diffraction tube can be used to investigate how the de Broglie wavelength of electrons depends on their speed

• To observe the diffraction of electrons, they must be focused through a gap similar to their de Broglie wavelength, such as an atomic lattice

  • Graphite film is ideal for this purpose because of its crystalline structure

  • The gaps between neighbouring planes of the atoms in the crystals act as slits, allowing the electron waves to spread out and create a diffraction pattern

  • This phenomenon is similar to the diffraction pattern produced when light passes through a diffraction grating

  • If the electrons acted as particles, a pattern would not be observed, instead, the particles would be distributed uniformly across the screen. The diffraction pattern is observed on the screen as a series of concentric rings

• It is observed that:

  • a larger accelerating voltage reduces the diameter of a given ring

  • a lower accelerating voltage increases the diameter of the rings

• As the voltage is increased:

  • The speed of the electrons is increased, therefore:

    • the momentum of the electrons is increased

    • the kinetic energy of the electrons is increased

    • the de Broglie wavelength is decreased

  • The angle of diffraction is decreased, therefore:

    • the radius of the diffraction pattern is decreased

• Electron diffraction was the first clear evidence that matter can behave like light and has wave properties

• The de Broglie wavelength can be used to calculate the angle of the first maximum in the diffraction pattern

$n\lambda =d\sin \theta \Rightarrow \sin \theta =\frac{\lambda }{d}$

• Where:

  • $\theta$ = angle of diffraction of the first maximum

  • $\lambda$ = de Broglie wavelength

  • $d$ = spacing between atoms used for diffraction

• The first minimum:

  • will be half the value of the first maximum

  • will not be zero

• Subsequent minima reduce in intensity until reaching zero