Charged Particles in Magnetic Fields (DP IB Physics)

Charged Particles in Magnetic Fields

• When a charged particle enters a uniform magnetic field, it travels in a circular path

• This is because the direction of the magnetic force F will always be

  • perpendicular to the particle's velocity v

  • directed towards the centre of the path, resulting in circular motion

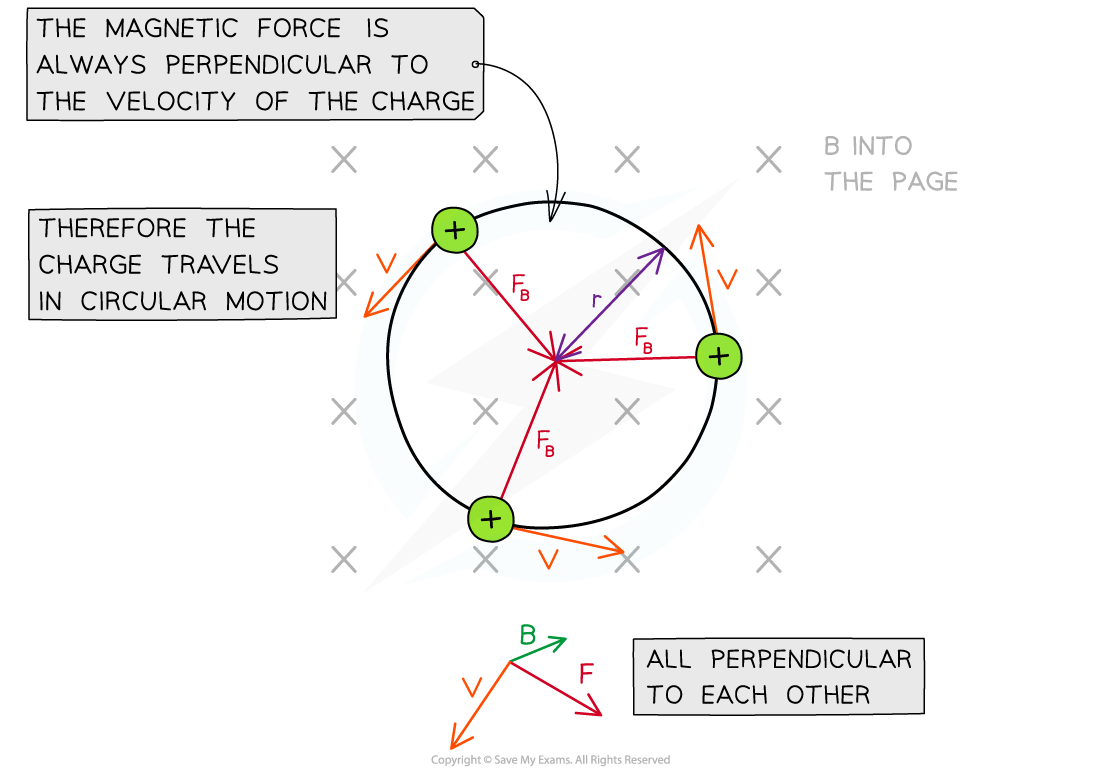
In a magnetic field, a charged particle travels in a circular path as the force, velocity and field are all perpendicular

• The magnetic force F provides the centripetal force on the particle

• The equation for centripetal force is:

• Equating this to the magnetic force on a moving charged particle gives the expression:

• Rearranging for the radius r gives an expression for the radius of the path of a charged particle in a perpendicular magnetic field:

• Where:

  • r = radius of the path (m)

  • m = mass of the particle (kg)

  • v = linear velocity of the particle (m s⁻¹)

  • B = magnetic field strength (T)

  • Q = charge of the particle (C)

• This equation shows that:

  • Faster moving particles with speed v move in larger circles (larger r): 

  • Particles with greater mass m move in larger circles: 

  • Particles with greater charge q move in smaller circles:  

  • Particles moving in a strong magnetic field B move in smaller circles: 

• The centripetal acceleration is in the same direction as the magnetic (centripetal) force

• This can be found using Newton's second law: