Charged Particles in Electric & Magnetic Fields (DP IB Physics) : Revision Note
Charged Particles in Electric & Magnetic Fields
A charged particle moving in perpendicularly orientated uniform electric and magnetic fields will experience
a force parallel to the electric field
a force perpendicular to the magnetic field
One particular orientation is:
a charged particle moving with speed v to the right of the x-axis
an electric field E directed up the y-axis
a magnetic field B directed out of the page on the z-axis
Hence, the three vectors are perpendicular to each other
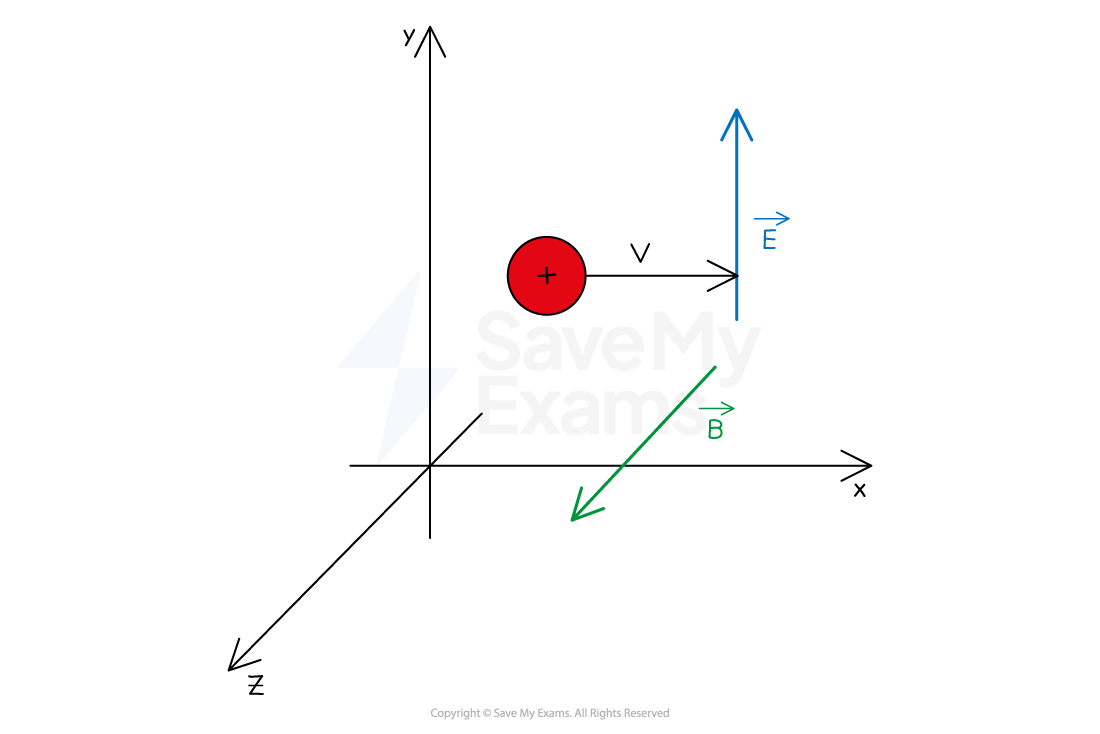
An example of the orientation of an electric field perpendicular to a magnetic field
Motion of a Positively Charged Particle
When the particle is positively charged
the electric force acts upwards, in the same direction as the electric field
the magnetic force acts downwards, perpendicular to the magnetic field
Using Fleming's left hand rule:
Field (first finger): the magnetic field is directed out of the page
Current (second finger): the positive charge moves to the right
Force (thumb): the magnetic force acts downwards
Hence, the electric force and magnetic force act in opposite directions on the positive charge
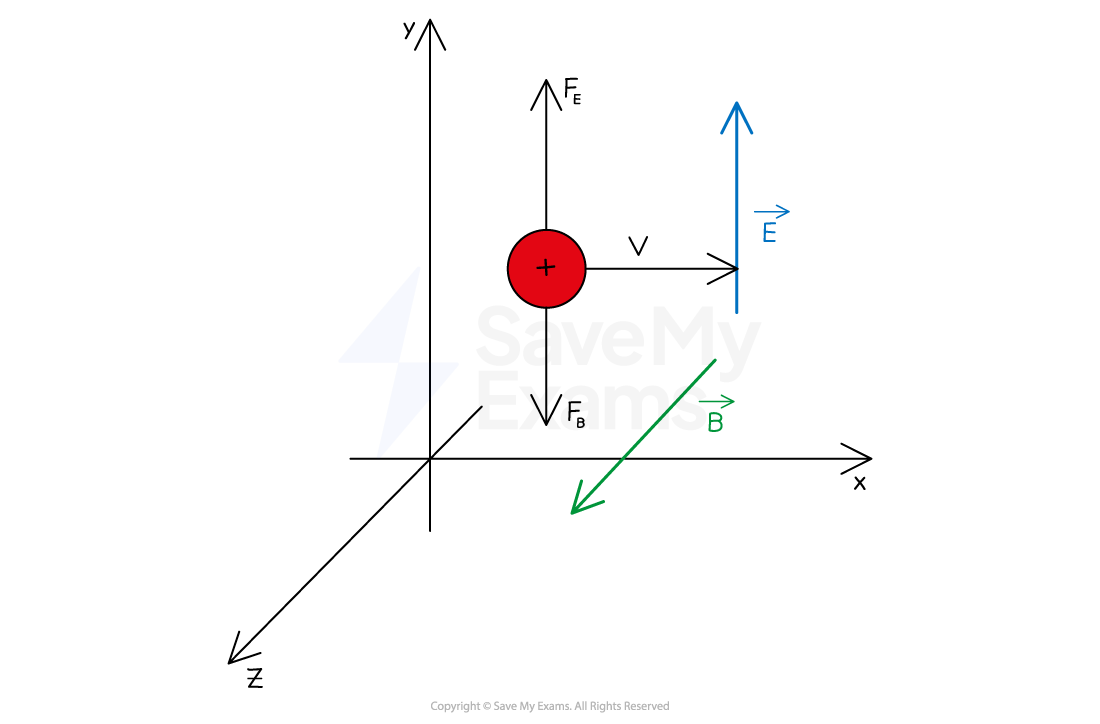
The electric force acts up the page and the magnetic force acts in the opposite direction down the page
Motion of a Negatively Charged Particle
When the particle is negatively charged
the electric force acts downwards, in the opposite direction to the electric field
the magnetic force acts upwards, perpendicular to the magnetic field
Using Fleming's left hand rule:
Field (first finger): the magnetic field is directed out of the page
Current (second finger): the positive charge moves to the left (since the negative charge moves to the right, in the opposite direction)
Force (thumb): the magnetic force acts upwards
Hence, the electric force and magnetic force act in opposite directions on the negative charge
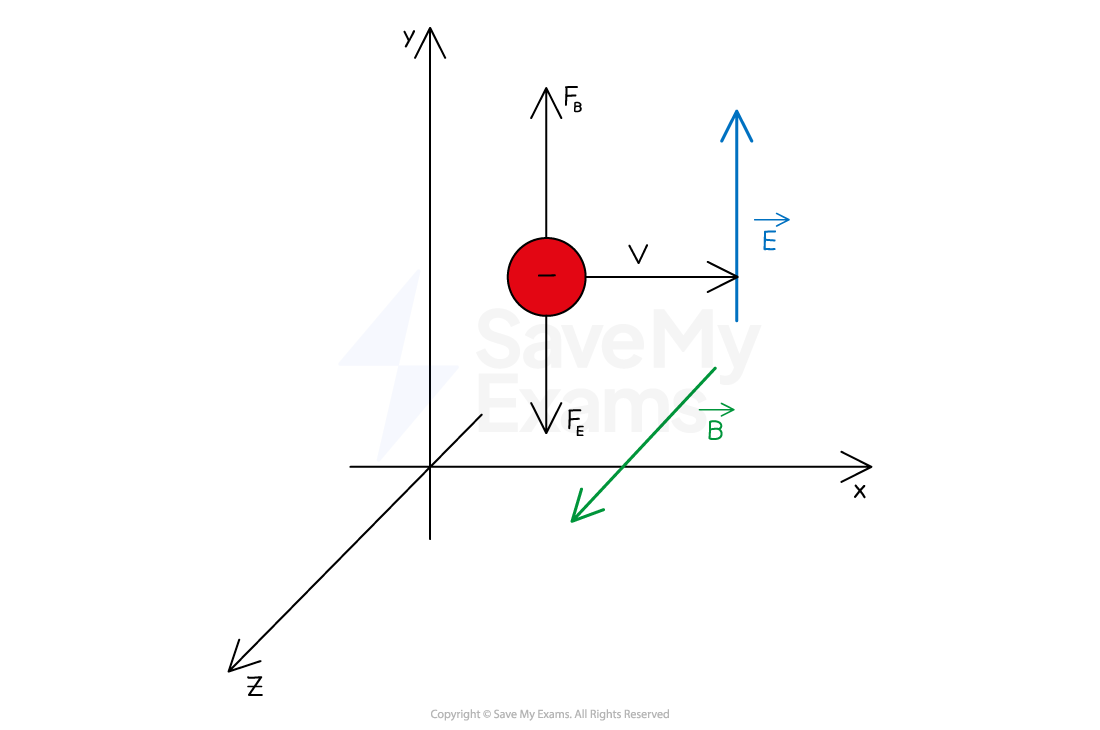
The magnetic force acts up the page and the electric force acts in the opposite direction down the page
Balancing the Electric and Magnetic Fields
The field strengths of each field can be adjusted until the forces cancel each other out
If the magnitude of the electric and magnetic forces are equal, the particle will move in a straight line with constant speed
This speed can be determined by equating the two forces:
Where:
The electric force on the particle:
The magnetic force on the particle:
Equating these and rearranging for speed v gives:
Therefore, the speed v is equal to the ratio of the electric and magnetic field strengths
Worked Example
An electron passes between two parallel metal plates moving with a constant velocity of 2.1 × 107 m s−1. The potential difference between the plates is 3100 V. A uniform magnetic field of magnitude 0.054 T acts perpendicular to the electric field and the movement of the electron.
The electric field acts to the right and the electron is moving downwards.
(a) Determine the direction of the magnetic field
(b) Calculate the separation of the plates
Answer:
(a) The direction of the magnetic field:
Step 1: Draw a diagram of the situation
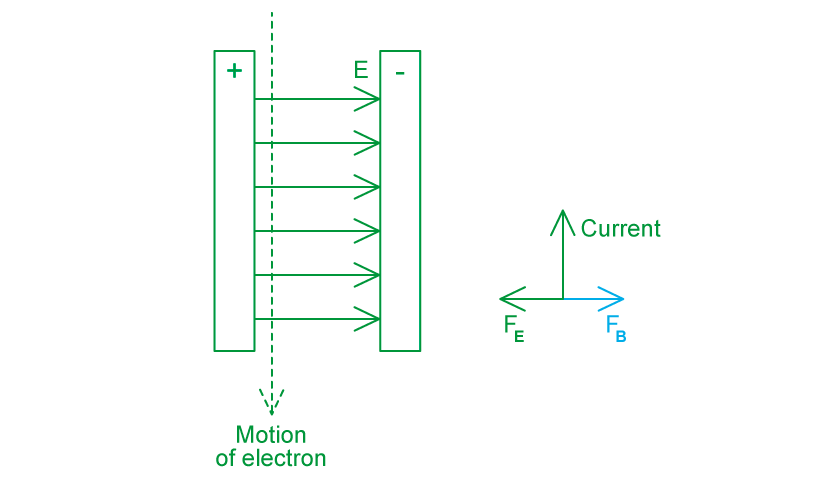
The electric field goes (from the positive plate to the negative plate), to the right
The electron is moving vertically downwards
So, the current is moving upwards in the opposite direction to the electron
The electric force is acting in the opposite direction to the electric field because the particle is an electron
Step 2: Determine the direction of the magnetic field
The electron is moving at a constant speed, so the magnetic and electric forces are equal and opposite
Hence, the magnetic force acts to the left
(b) Calculate the separation of the plates:
Step 1: Calculate the magnitude of the electric field, E
Step 2: Calculate the separation of the plates
Use the electric field strength equation:
m
Examiner Tips and Tricks
Take time to consider the direction of all components of the electric and magnetic fields.
Remember that the electric and magnetic forces act in the opposite direction for negatively charged particles compared to positively charged.
The direction of the charge in Fleming's left hand rule is always the direction of positive charge. This should be in the opposite direction if the particle has a negative charge!
Charge to Mass Ratio of Particles
The charge-to-mass ratio of a particle is defined as:
The ratio of the total charge of a particle to its mass
It can be calculated using the equation:
charge-to-mass ratio =
The charge-to-mass ratio of an electron is
C kg−1
The charge-to-mass ratio of a proton is
C kg−1
Determining Charge-to-Mass Ratio
The charge-to-mass ratio of a charged particle can be determined by investigating its path in a uniform magnetic field
The method used by J.J. Thomson to determine the charge-to-mass ratio of an electron used:
'Helmholtz coils' to generate a uniform magnetic field
oppositely charged parallel plates to generate a uniform electric field
Apparatus of the J.J. Thomson Experiment
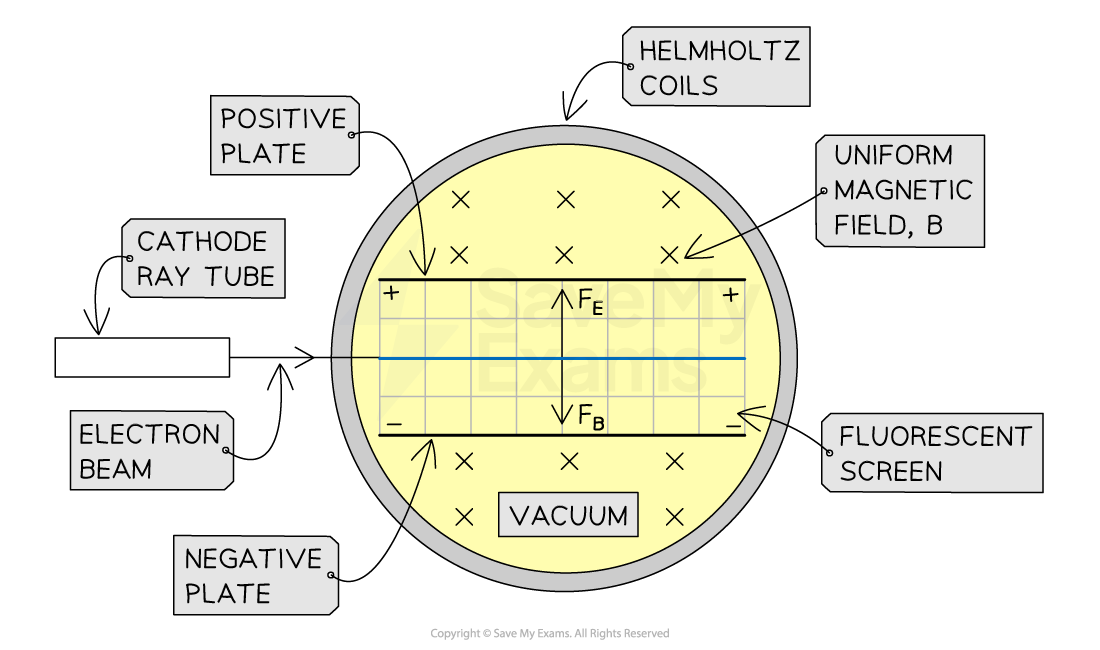
The magnetic field generates a downward force, the electric field between the plates generates an upward force - the fluorescent screen shows a straight beam when these two forces are equal and opposite
When moving in a magnetic field, a charge experiences a force perpendicular to its motion
From the diagram above, the magnetic field B is directed into the plane of the page
From Fleming's left-hand rule, the magnetic force FB on an electron acts downwards
When moving in a uniform electric field, a charge experiences a force towards either the positive or negative plate
The electrons are negative so they experience an upward electric force FE towards the positive plate
When these forces are equal in magnitude, the beam of electrons is horizontal and straight
The electric field strength between two parallel plates is given by:
The electric force can be adjusted by changing the potential difference V across the plates
Therefore, the upward electric force FE is equal to:
Where:
q = charge of the particle (C)
V = potential difference between the plates (V)
d = separation between the plates (m)
The upward electric force is adjusted until it is equal to the downward magnetic force, making the electron beam horizontal:
The downward magnetic force FB on the particle is equal to:
Where:
v = speed of the particle (m s−1)
B = magnetic field strength (T)
Equating the two forces and rearranging for particle speed v:
If the electric field is switched off, the beam will be influenced by the magnetic field only
The particles will then travel in a circular path with the same speed v
Electron beam in a magnetic field
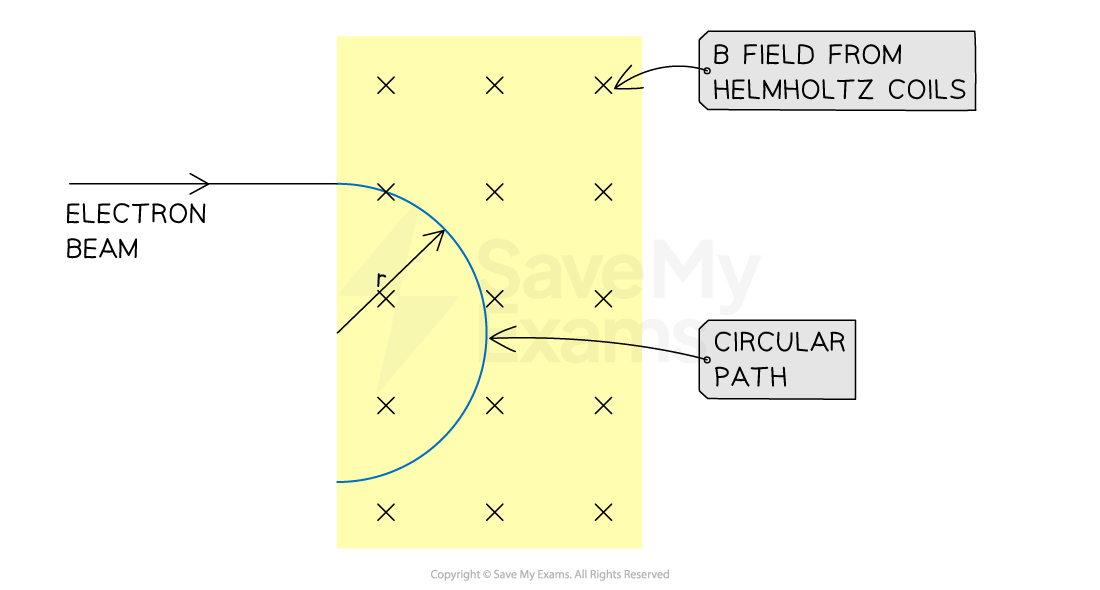
The radius of the electron beam's circular path can be measured to calculate the charge-to-mass ratio of an electron
The radius of the circular path of a charged particle in a magnetic field is given by:
Where:
r = radius of the path (m)
m = mass of the particle (kg)
Rearranging for the charge-to-mass ratio:
To measure these quantities:
the radius r of the path and the magnetic field strength B can be measured directly
the speed v of the particles can determined using perpendicular electric and magnetic fields
Combining these two equations gives an expression for the charge-to-mass ratio of a charged particle:
Therefore, these four quantities
are needed to determine a particle's charge-to-mass ratio.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
