AC Generators (DP IB Physics: HL): Revision Note

The AC generator

• If a coil of wire is rotated inside a magnetic field by an external force, an e.m.f. will be generated in the wire which causes current to flow within the coil

• A simple A.C. generator converts mechanical energy into electrical energy in the form of alternating current

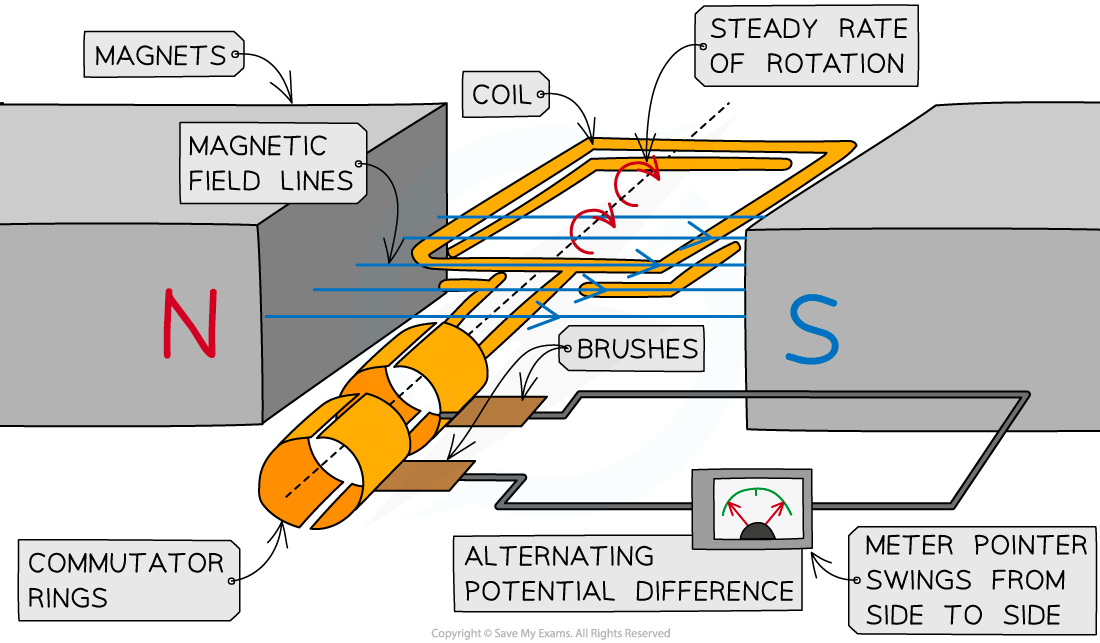
An alternator is a rotating coil in a magnetic field connected to commutator rings

• A rectangular coil is forced to spin in a uniform magnetic field

• The coil is connected to a centre-reading meter by metal brushes that press on two metal slip rings (or commutator rings)

  • The slip rings and brushes provide a continuous connection between the coil and the meter

• When the coil turns in one direction:

  • The pointer defects first one way, then the opposite way, and then back again

  • This is because the coil cuts through the magnetic field lines and a potential difference, and therefore current, is induced in the coil

• The pointer deflects in both directions because the current in the circuit repeatedly changes direction as the coil spins

  • This is because the induced potential difference in the coil repeatedly changes its direction

  • This continues as long as the coil keeps turning in the same direction

• The induced potential difference and the current alternate because they repeatedly change direction

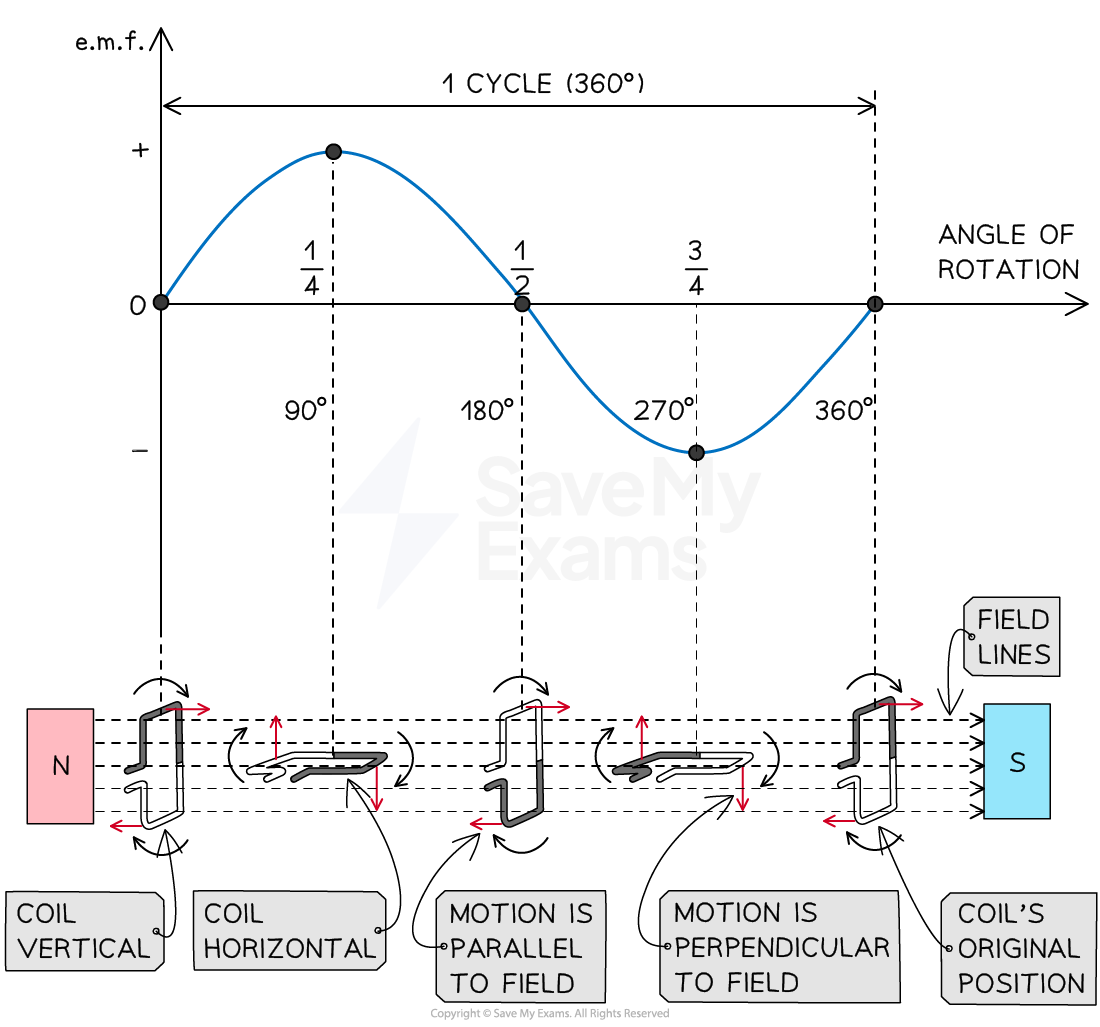
As the coil rotates in the magnetic field, the changing magnetic flux causes the induction of e.m.f. in the opposite sides of the coil

Emf Induction in a Rotating Coil

• When a coil rotates in a uniform magnetic field, the flux through the coil will vary as it rotates

• Since e.m.f is the rate of change of flux linkage, this means the e.m.f will also change as it rotates 

  • The maximum e.m.f is when the coil cuts through the most field lines

  • The e.m.f induced is an alternating voltage

• Flux linkage is given by

$N\Phi =BAN\cos \theta$

• Angular speed ω is defined as the rate of change of angular displacement, so

$\omega =\frac{\theta }{t}$

• Therefore, for a rotating coil, the angle θ depends on the angular speed of the coil ω:

$\theta =\omega t$

• Hence, flux linkage can also be written as:

$N\Phi =BAN\cos \omega t$

• Where:

  • $N\Phi$ = flux linkage (Wb turns)

  • B = magnetic flux density (T)

  • A = cross-sectional area of the coil (m²)

  • N = number of turns of coil

  • ω = angular speed of the coil (rad s^-1)

  • t = time (s)

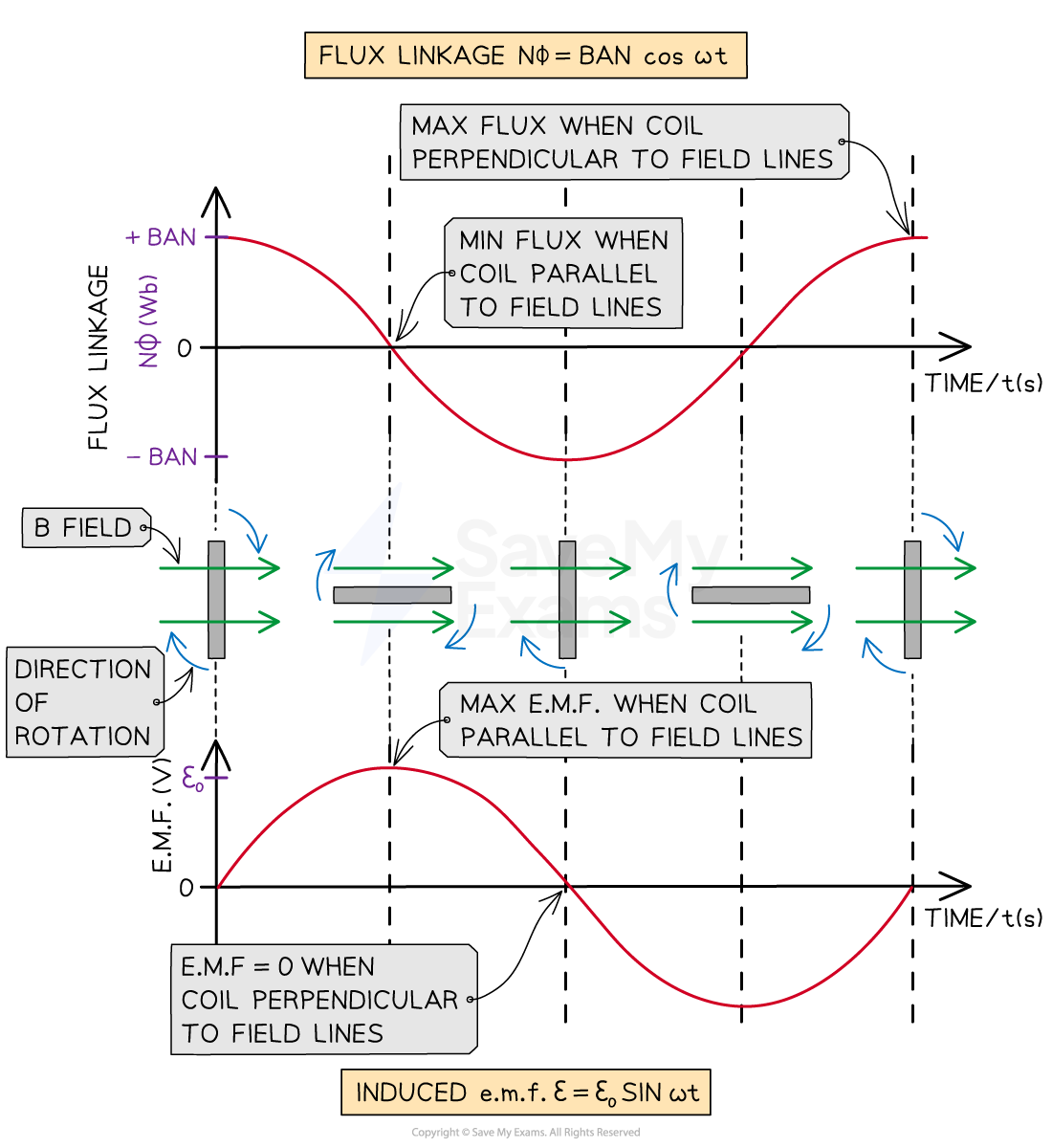
Flux linkage and induced e.m.f. in a rotating coil

• The graph shows that

  • The induced e.m.f varies sinusoidally and it is 90° out of phase with the flux linkage

• Mathematically, the induced e.m.f. can also be written as:

$\epsilon ={\epsilon }_0\sin \omega t$

$\epsilon =BAN\omega \sin \omega t$

• Where:

  • ε = e.m.f induced in the coil (V)

  • ε₀ = maximum e.m.f induced in the coil (V)

• The size of the induced e.m.f. in a rotating coil can be increased by increasing the frequency of rotation of the coil

• Increasing the coil's frequency of rotation increases:

  • The frequency of the alternating voltage

  • The amplitude of the alternating voltage

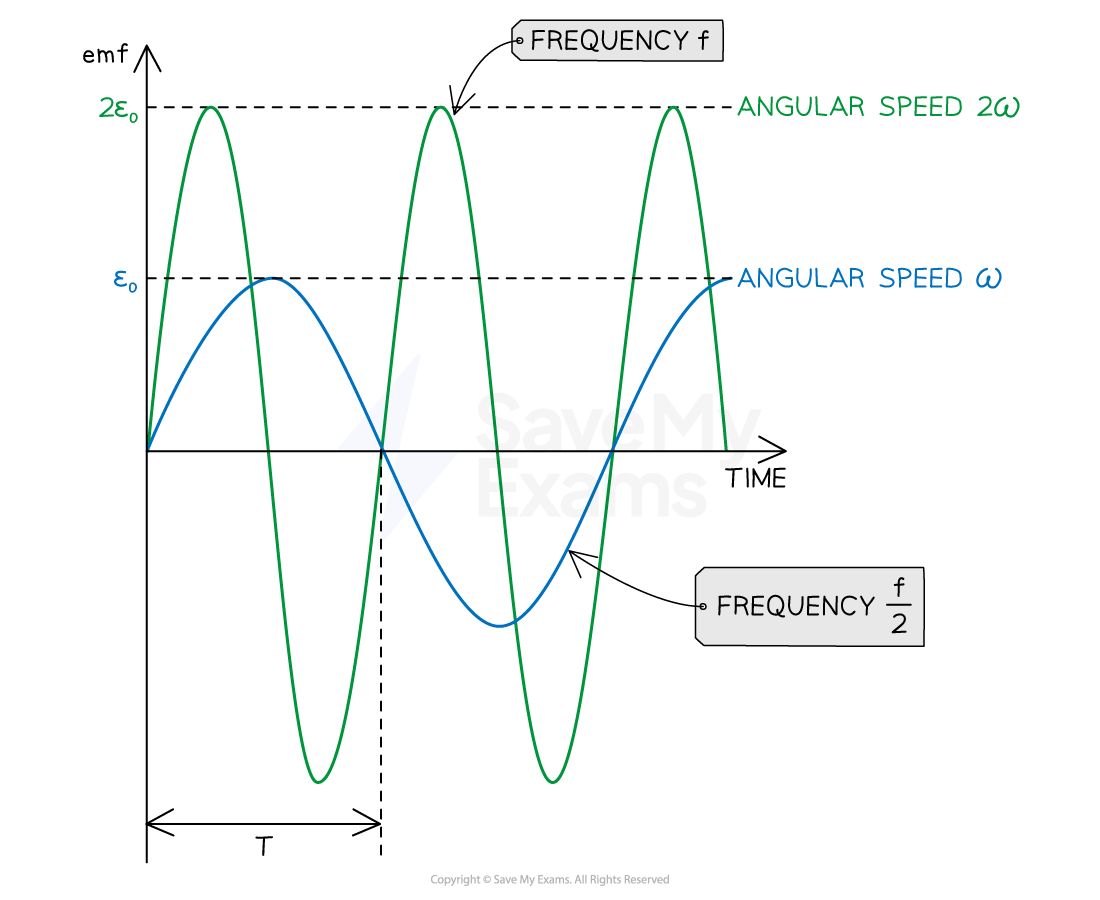
Doubling the angular speed of the rotating coil in a magnetic field doubles the size of the induced e.m.f. (double the amplitude) and the frequency of the rotation (half the time period)