IBPhysicsDPHLRevision NotesFieldsGravitational FieldsOrbital Motion, Speed & Energy

Orbital Motion, Speed & Energy (DP IB Physics: HL): Revision Note

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on 2 July 2026

Orbital Motion, Speed & Energy

Since most planets and satellites have near-circular orbits, the gravitational force F_G between two bodies (e.g. planet & star, planet & satellite) provides the centripetal force needed to stay in an orbit
- Both the gravitational force and centripetal force are perpendicular to the direction of travel of the planet

Consider a satellite with mass m orbiting Earth with mass M at a distance r from the centre travelling with linear speed v

$F_{G} = F_{c i r c}$

Equating the gravitational force to the centripetal force for a planet or satellite in orbit gives:

$\frac{G M m}{r^{2}} = \frac{m v^{2}}{r}$

The mass of the satellite m will cancel out on both sides to give:

$v^{2} = \frac{G M}{r} \Rightarrow v_{o r b i t a l} = \sqrt{\frac{G M}{r}}$

Where:
- $v_{o r b i t a l}$ = orbital speed of the smaller mass (m s⁻¹)
- G = Newton's Gravitational Constant
- M = mass of the larger mass being orbited (kg)
- r = orbital radius (m)

This means that all satellites, whatever their mass, will travel at the same speed v in a particular orbit radius r
- Since the direction of a planet orbiting in circular motion is constantly changing, the centripetal acceleration acts towards the planet

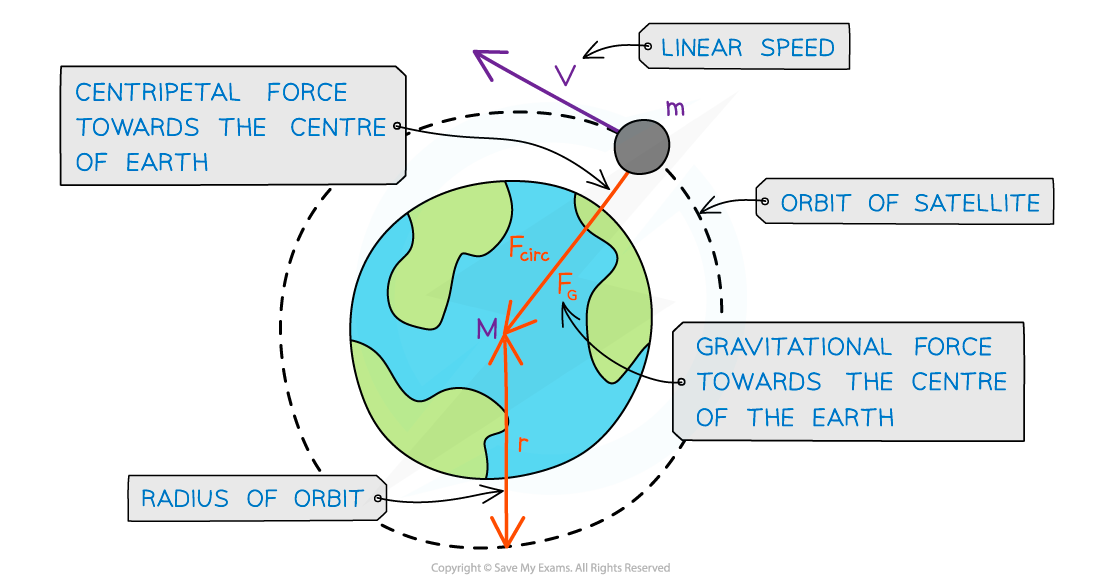
Circular motion satellite, downloadable AS & A Level Physics revision notes

A satellite in orbit around the Earth travels in circular motion

Energy of an Orbiting Satellite

An orbiting satellite follows a circular path around a planet
Just like an object moving in circular motion, it has both kinetic energy (E_k) and gravitational potential energy (E_p) and its total energy is always constant
An orbiting satellite's total energy is calculated by:

Total energy = Kinetic energy + Gravitational potential energy

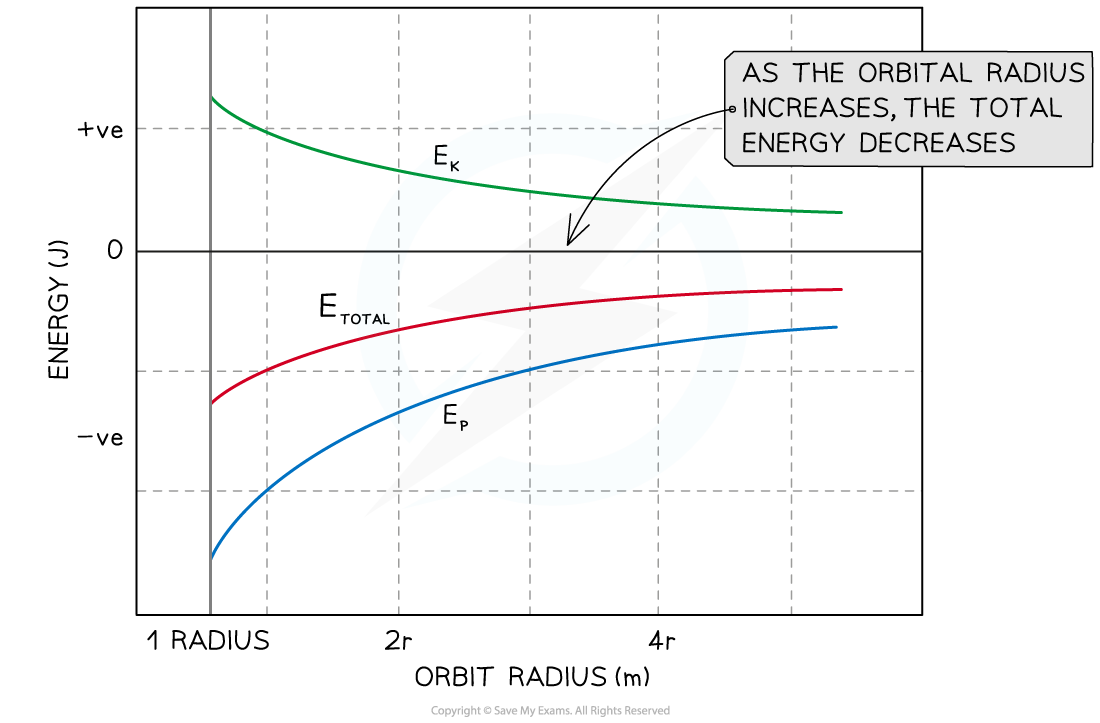
A graph showing the kinetic, potential and total energy for a mass at varying orbital distances from a massive body

This means that the satellite's E_k and E_p are also both constant in a particular orbit
- If the orbital radius of a satellite decreases its E_kincreases and its E_pdecreases
- If the orbital radius of a satellite increases its E_kdecreases and its E_pincreases

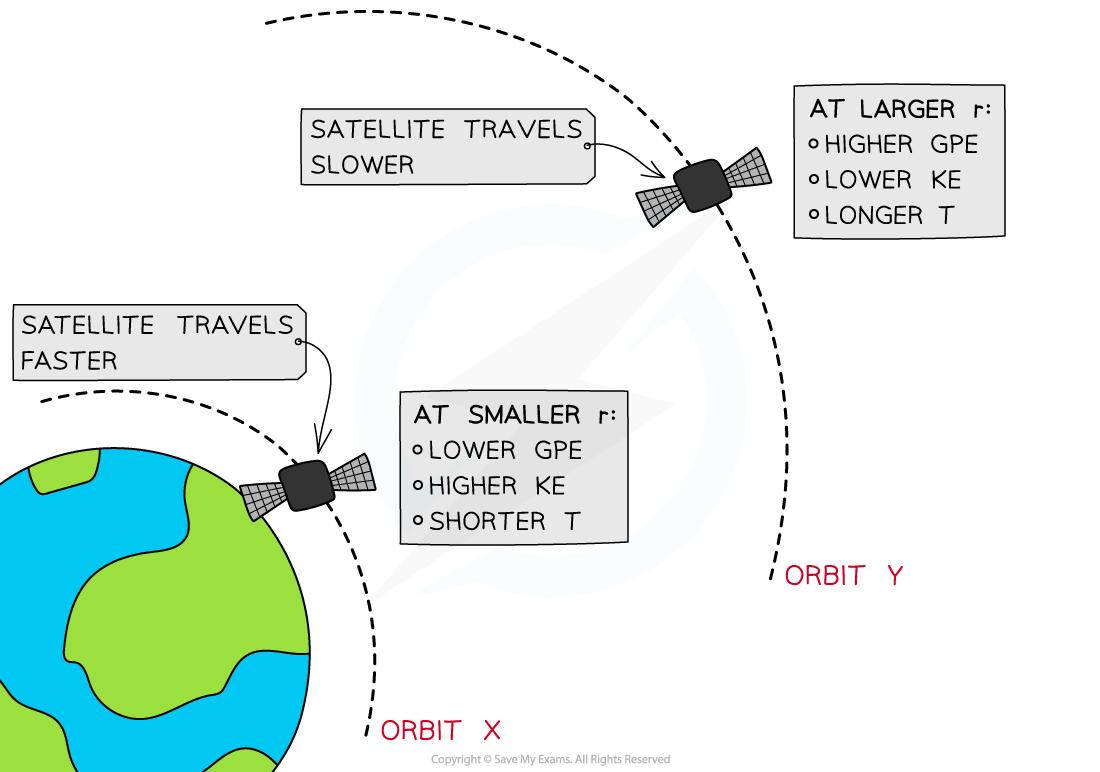
Energy of Orbiting Satellite, downloadable AS & A Level Physics revision notes

At orbit Y, the satellite has greater GPE and less KE than at at orbit X

A satellite is placed in two orbits, X and Y, around Earth
At orbit X, where the radius of orbit r is smaller, the satellite has a:
- Larger gravitational force on it
- Higher speed
- Higher E_k
- Lower E_p
- Shorter orbital time period, T
At orbit Y, where the radius of orbit r is larger, the satellite has a:
- Smaller gravitational force on it
- Smaller speed
- Lower E_k
- Higher E_p
- Longer orbital time period, T

Worked Example

A binary star system constant of two stars orbiting about a fixed point B.

The star of mass M₁ has a circular orbit of radius R₁ and mass M₂ has a radius of R₂. Both have an angular speed ⍵ about B.

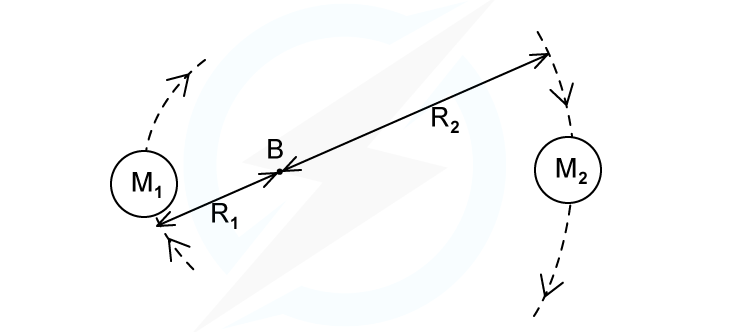
Worked example - circular orbits in g fields, downloadable AS & A Level Physics revision notes

In terms of G, M₂, R₁ and R₂, write an expression for

(a) the angular speed ⍵ of mass M₁

(b) the time period T of each star

Answer:

(a) Angular speed:

The centripetal force on mass M₁ is:

$F = \frac{M_{1} {v_{1}}^{2}}{R_{1}} = \frac{M_{1} {(ω R_{1})}^{2}}{R_{1}} = M_{1} R_{1} ω^{2}$

The gravitational force between the two masses is:

$F = \frac{G M_{1} M_{2}}{{(R_{1} + R_{2})}^{2}}$

Equating these expressions gives:

$M_{1} R_{1} ω^{2} = \frac{G M_{1} M_{2}}{{(R_{1} + R_{2})}^{2}}$

Rearrange for angular velocity

$ω = \sqrt{\frac{G M_{2}}{R_{1} {(R_{1} + R_{2})}^{2}}}$

(b) Orbital period:

The relation between angular speed and orbital period is

$ω = \frac{2 π}{T} \Rightarrow T = \frac{2 π}{ω}$

Using the expression for angular velocity from part (a)

$T = 2 π \div \sqrt{\frac{G M_{2}}{R_{1} {(R_{1} + R_{2})}^{2}}} = 2 π \sqrt{\frac{R_{1} {(R_{1} + R_{2})}^{2}}{G M_{2}}}$

Worked Example

Two identical satellites, X and Y, orbit a planet at radii R and 3R respectively.

Which one of the following statements is incorrect?

A. Satellite X has more kinetic energy and less potential energy than satellite Y

B. Satellite X has a shorter orbital period and travels faster than satellite Y

C. Satellite Y has less kinetic energy and more potential energy than satellite X

D. Satellite Y has a longer orbital period and travels faster than satellite X

Answer: D

Satellite Y is at a larger orbital radius, therefore it will have a longer orbital period, since $T^{2} \propto R^{3}$
Being at a larger orbital radius means the gravitational force will be weaker for Y than for X
So, satellite Y will travel much slower than X as centripetal force: $F \propto v^{2}$
Travelling at a slower speed means satellite Y will have less kinetic energy, as $E_{K} \propto v^{2}$ , and, therefore, more potential energy than X

Satellite X

Satellite Y

orbital radius

orbital period

orbital speed

kinetic energy

potential energy

smaller

shorter

faster

greater

lower

larger

longer

slower

lower

greater

Therefore, all statements are correct except in D where it says 'Satellite Y travels faster than satellite X'

Examiner Tips and Tricks

If you can't remember which way around the kinetic and potential energy increases and decreases, think about the velocity of a satellite at different orbits.

When it is orbiting close to a planet, it experiences a larger gravitational pull and therefore orbits faster. Since the kinetic energy is proportional to v², it, therefore, has higher kinetic energy closer to the planet. To keep the total energy constant, the potential energy must decrease too.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent

Orbital Motion, Speed & Energy (DP IB Physics: HL): Revision Note

Orbital Motion, Speed & Energy

Energy of an Orbiting Satellite

Worked Example

Worked Example

Examiner Tips and Tricks

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M

Reviewer: Caroline Carroll