Electric Potential (DP IB Physics) : Revision Note
Electric Potential
The electric potential at a point is defined as:
The work done per unit charge in taking a small positive test charge from infinity to a defined point
Electric potential is measured in J C−1 or V
It is a scalar quantity but has a positive or negative sign to indicate the sign of the charge
In a similar way to gravitational potential, electric potential also has a value of zero at infinity
The electric potential at a point depends on:
The magnitude of the point charge
The distance between the charge and the point
Electric potential for a positive charge
Around an isolated positive charge, electric potential:
has a positive value
increases when a test charge moves closer
decreases when a test charge moves away
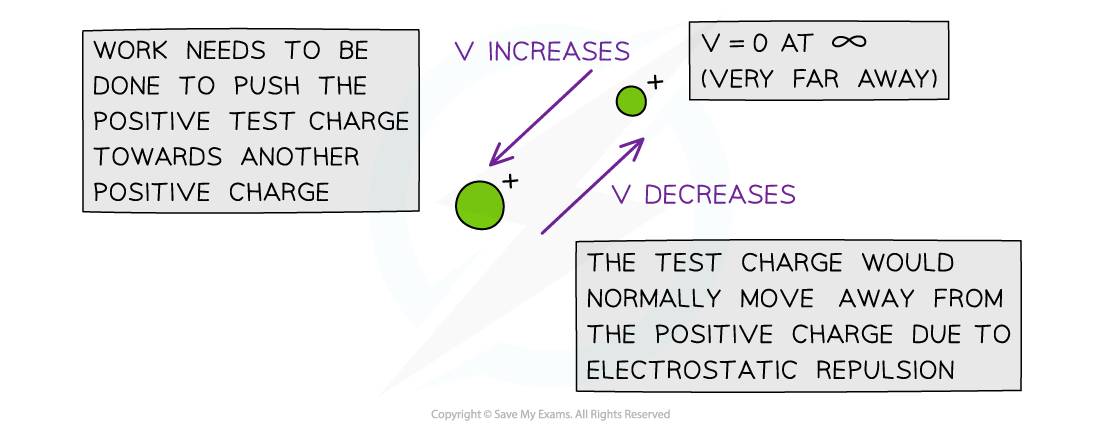
For a positive charge, the electric potential decreases in the direction a positive test charge would move in due to the electrostatic repulsion
Electric potential for a negative charge
Around an isolated negative charge, electric potential:
has a negative value
decreases when a test charge moves closer
increases when a test charge moves away

For a negative charge, the electric potential decreases in the direction a positive test charge would move in due to the electrostatic attraction
Examiner Tips and Tricks
One way to remember whether the electric potential increases or decreases with respect to the distance from the charge is by the direction of the electric field lines. The potential always decreases in the same direction as the field lines and vice versa.
Calculating Electric Potential
The electric potential around a point charge can be calculated using:
Where:
Ve = electric potential (V)
Q = magnitude of the charge producing the potential (C)
k = Coulomb constant (N m2 C−2)
r = distance from the centre of the point charge (m)
For a positive (+) charge:
potential Ve increases as the separation r decreases
energy must be supplied to a positive test charge to overcome the repulsive force
For a negative (−) charge:
potential Ve decreases as the separation r increases
energy is released as a positive test charge moves in the direction of the attraction force
The electric potential has an inversely proportional relationship with distance
Unlike gravitational potential which is always negative, the sign of the charge corresponds to the sign of the electric potential
Note: this equation also applies to a conducting sphere. The charge on the sphere is treated as if it is concentrated at the centre of the sphere, i.e. like a point charge
Graph of potential against distance for a positive charge
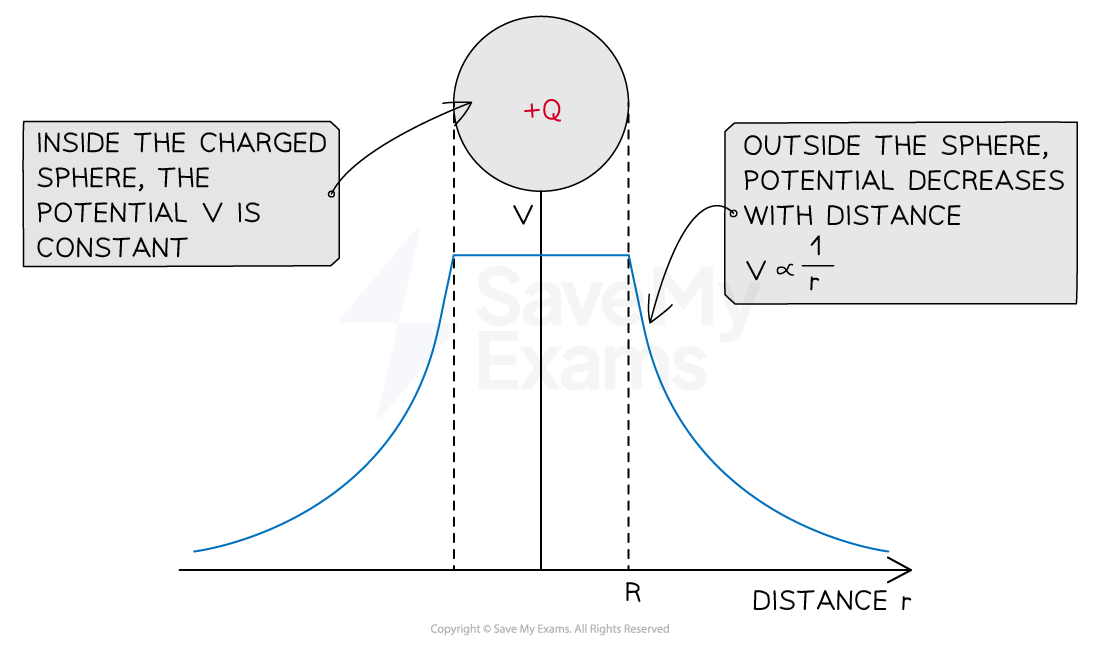
Electric potential is constant inside a charged sphere and decreases with distance outside the sphere
Combining Electric Potentials
To find the potential at a point caused by multiple charges, each potential can be combined by addition
For example, the combined potential of two point charges at a point is:
Where:
Q1, Q2 = magnitude of the charges (C)
r1, r2 = distance between each charge and the point (m)
How to determine resultant electric potential
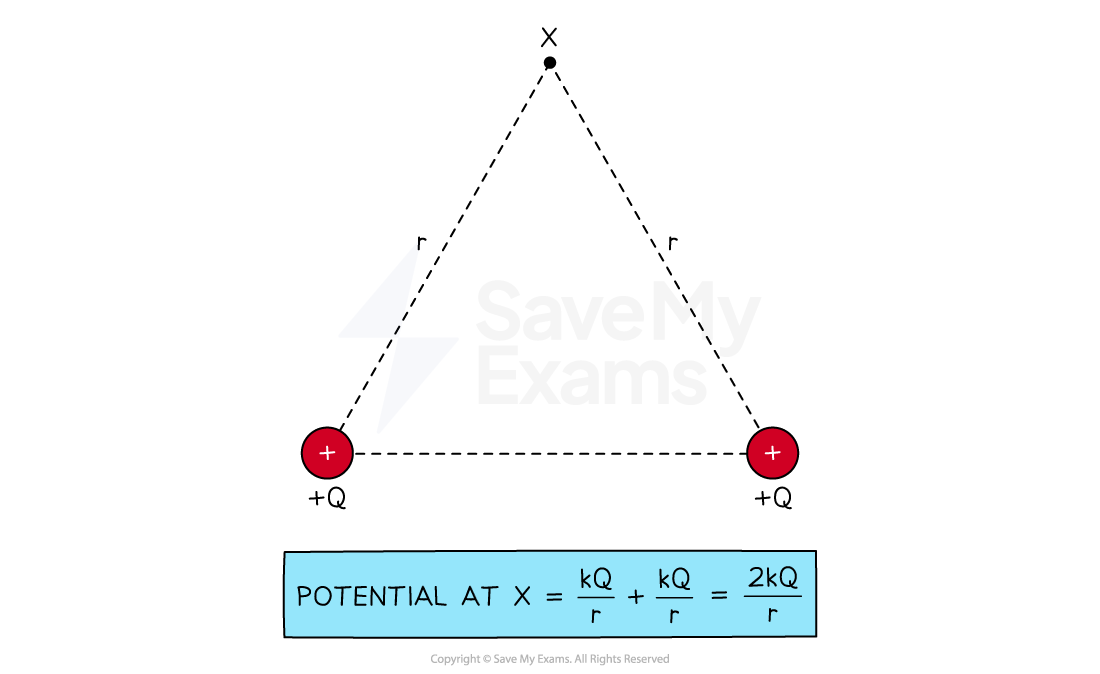
Point X makes an equilateral triangle of length r with two equal positive charges Q. The combined potential of both charges at X is double the potential due to one of the charges
Worked Example
A Van de Graaff generator has a spherical dome of radius 15 cm. It is charged up to a potential of 240 kV.
Calculate
(a) the charge stored on the dome
(b) the potential at a distance of 30 cm from the dome
Answer:
Part (a)
Step 1: List down the known quantities
Radius of the dome, r = 15 cm = 15 × 10−2 m
Potential difference, V = 240 kV = 240 × 103 V
Coulomb constant, k = 8.99 × 109 N m2 C−2
Step 2: Write down the equation for the electric potential due to a point charge
Step 3: Rearrange for charge Q
Step 4: Substitute in values
μC
Part (b)
Step 1: Write down the known quantities
Charge stored in the dome, Q = 4.0 × 10−6 C
Distance, r = radius of the dome + distance from the dome = 15 + 30 = 45 cm = 0.45 m
Note: we are treating the Van de Graaff as a point charge, so we take the distance from the centre of the dome
Step 2: Write down the equation for electric potential due to a point charge
Step 3: Substitute in values
kV (2 s.f.)

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
