Revision NotesExam QuestionsFlashcards
IBPhysicsHLRevision NotesWave BehaviourSimple Harmonic MotionTime Period of a Mass–Spring System

Syllabus Edition

First teaching 2023

First exams 2025

|

Time Period of a Mass–Spring System (HL IB Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Time Period of a Mass–Spring System

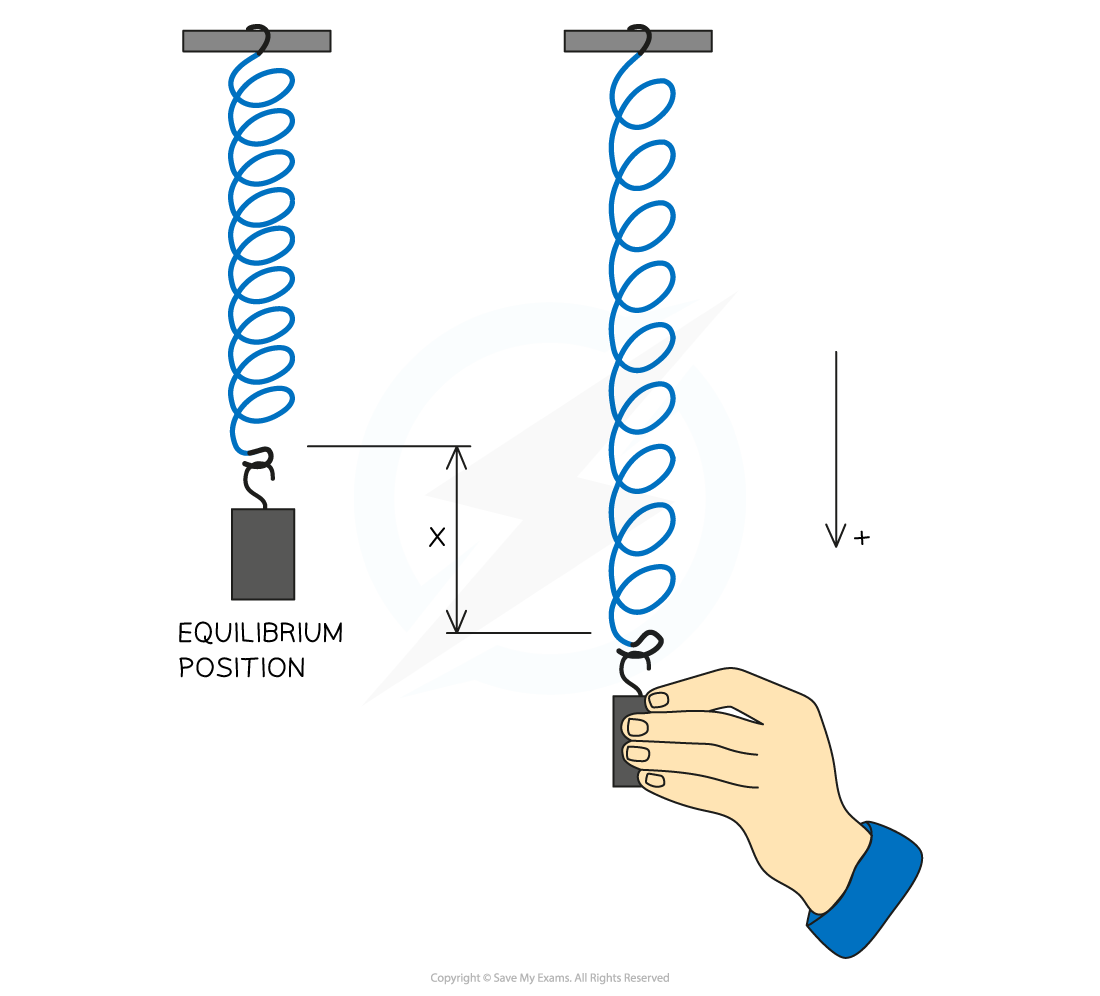
  • A mass-spring system consists of a mass attached to the end of a spring
  • The equation for the restoring force (the force responsible for the SHM) is FH = - kx 
 13-3-mass-spring-example_edexcel-al-physics-rn
  • The time period of a mass-spring system is given by:

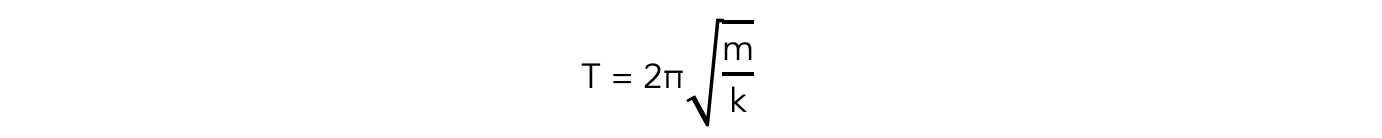
Mass-Spring Time Period Equation

  • Where:
    • T = time period (s)
    • m = mass on the end of the spring (kg)
    • k = spring constant (N m-1)

  • This equation applies to both horizontal and vertical mass-spring systems:

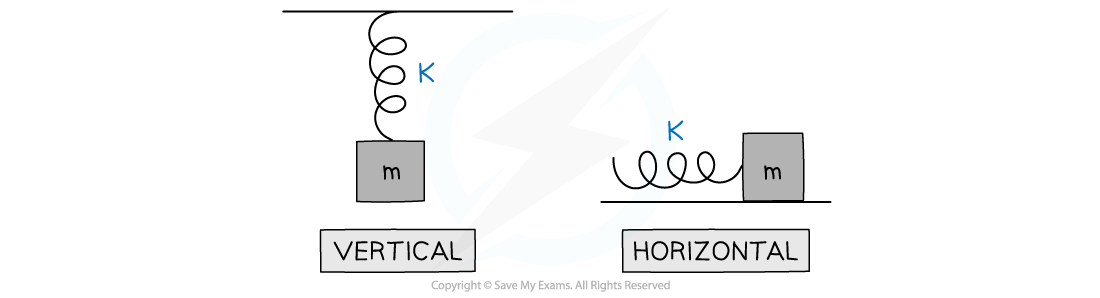
A mass-spring system can be either vertical or horizontal. The time period equation applies to both

  • The equation shows that the time period and frequency, of a mass-spring system, does not depend on the force of gravity
    • Therefore, the oscillations would have the same time period on Earth and the Moon

  • The higher the spring constant k, the stiffer the spring and the shorter the time period of the oscillation

Worked example

A 200 g toy robot is attached to a pole by a spring, which has a spring constant of 90 N m−1 and made to oscillate horizontally.

Calculate:

(a)
The force that acts on the robot when the spring is extended by 5 cm.
(b)
The acceleration of the robot whilst at its amplitude position.

 

Answer:

(a)

  • Consider the motion of the robot at the equilibrium and stretched (amplitude) positions:

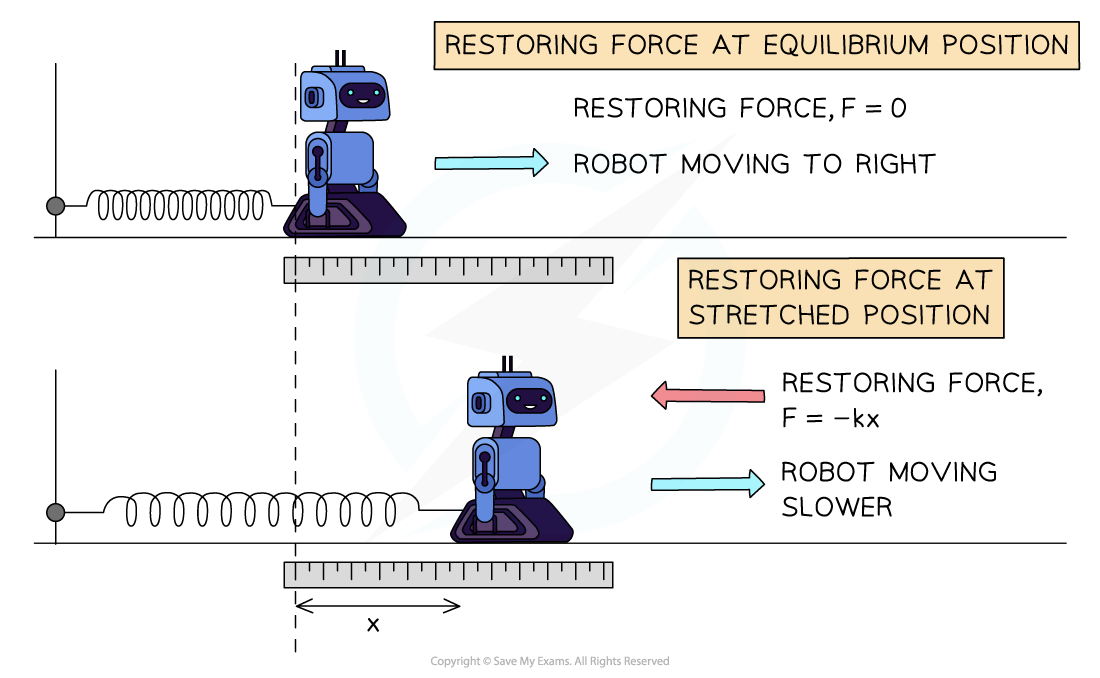
13-1-worked-example_edexcel-al-physics-rn

  • The restoring force is given by

F space equals space minus k x

  • Using:
    • Extension, x = 5 cm = 0.05 m
    • Spring constant, k = 90 N m−1

F = −90 × 0.05 = −4.5 N

  • A force of 4.5 N will act on the robot, trying to pull it back towards the equilibrium position. 

(b)

  • Newton's second law relates force and acceleration by

F space equals space m a

  • Using:
    • Mass, m = 200 g = 0.2 kg

a space equals space F over m = fraction numerator negative 4.5 over denominator 0.2 end fraction = −22.5 m s−2

  • The robot will decelerate at a rate of 22.5 m s−2 when at this amplitude position

Worked example

Calculate the frequency of a mass of 2.0 kg attached to a spring with a spring constant of 0.9 N m–1 oscillating with simple harmonic motion.

Answer:

Step 1: Write down the known quantities

  • Mass, m = 2.0 kg
  • Spring constant, k = 0.9 N m−1

Step 2: Write down the equation for the time period of a mass-spring system

T space equals space 2 pi square root of m over k end root

Step 3: Combine with the equation relating time period T and frequency, f

T space equals space 1 over f

1 over f space equals space 2 pi square root of m over k end root space space space space space rightwards double arrow space space space space space f space equals space fraction numerator 1 over denominator 2 straight pi end fraction square root of k over m end root

Step 4: Substitute in the values to calculate frequency

f space equals space fraction numerator 1 over denominator 2 straight pi end fraction square root of fraction numerator 0.9 over denominator 2 end fraction end root

Frequency:  f = 0.11 Hz

Examiner Tip

Another area of physics where you may have seen the spring constant k is from Hooke's Law. Exam questions commonly merge these two topics together, so make sure you're familiar with the Hooke's Law equation too.

In the second worked example, the frequency calculated is the natural frequency of the mass-spring system, a concept that comes up in the topic of resonance.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Simple Harmonic Motion (SHM)Next:Time Period of a Simple Pendulum
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.