Equations for the Doppler Effect of Sound (HL) | HL IB Physics Revision Notes 2025

The Doppler Effect of Sound

When a source of sound waves moves relative to a stationary observer, the observed frequency can be calculated using the equation below:

9-5-3-doppler-calculation-1-ib-hl

Doppler shift equation for a moving source

The wave velocity for sound waves is 340 ms^-1
The ± depends on whether the source is moving towards or away from the observer
- If the source is moving towards the observer, the denominator is v - u_s
- If the source is moving away from the observer, the denominator is v + u_s

When a source of sound waves remains stationary, but the observer is moving relative to the source, the observed frequency can be calculated using the equation below:

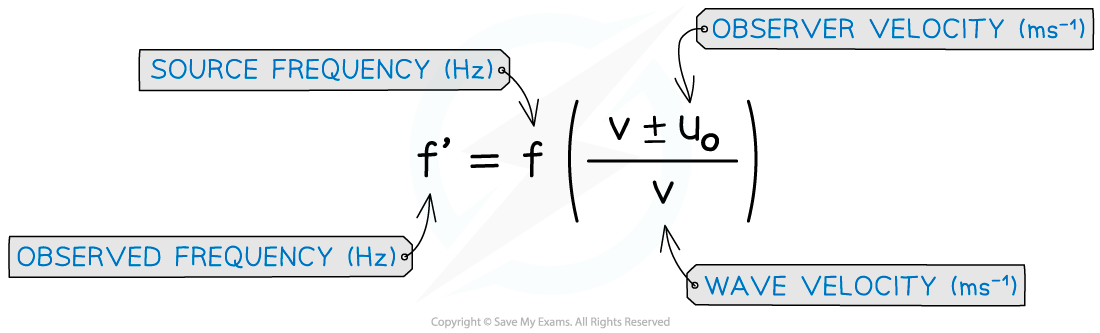
9-5-3-doppler-calculation-2-moving-observer-ib-hl

Doppler shift equation for a moving observer

The ± depends on whether the observer is moving towards or away from the source
- If the observer is moving towards the source, the numerator is v + u_o
- If the observer is moving away from the source, the numerator is v − u_o

These equations can also be written in terms of wavelength
- For example, the equation for a moving source is shown below:

Doppler shift equation for a moving source in terms of wavelength

The ± depends on whether the source is moving towards or away from the observer
- If the source is moving towards, the term in the brackets is $1 - \frac{u_{S}}{v}$
- If the source is moving away, the term in the brackets is $1 + \frac{u_{S}}{v}$

Worked example

A police car siren emits a sound wave with a frequency of 450 Hz. The car is travelling away from an observer at a speed of 45 m s⁻¹.

The speed of sound is 340 m s⁻¹.

What frequency of sound does the observer hear?

A. 519 Hz B. 483 Hz C. 397 Hz D. 358 Hz

WE - Doppler shift equation answer image

Worked example

A bank robbery has occurred and the alarm is sounding at a frequency of 3 kHz. The robber jumps into a car which accelerates and reaches a constant speed.

As he drives away at a constant speed, he hears the frequency of the alarm decrease to 2.85 kHz.

Determine the speed at which the robber must be driving away from the bank.

Speed of sound = 340 m s⁻¹

Answer:

Step 1: List the known quantities

Source frequency, $f$ = 3 kHz
Observed frequency, $f^{'}$ = 2.85 kHz
Speed of sound, $v$ = 340 m s⁻¹

Step 2: Write down the Doppler shift equation

The observer is moving away from a stationary source of sound, so the equation to use is

$f^{'} = f (\frac{v - u_{o}}{v})$

Step 3: Rearrange to find the desired quantity

$\frac{f^{'}}{f} = (\frac{v - u_{o}}{v}) \Rightarrow \frac{v f^{'}}{f} = v - u_{o}$

$\frac{v f^{'}}{f} + u_{o} = v \Rightarrow u_{o} = v - \frac{v f^{'}}{f}$

$u_{o} = v (1 - \frac{f^{'}}{f})$

Step 4: Substitute the values into the equation

$u_{o} = 340 \times (1 - \frac{2.85}{3}) = 17 m s^{- 1}$

The robber must be driving away at a constant speed of 17 m s⁻¹ based on the change in frequency heard

Examiner Tip

Pay careful attention as to whether you need to + or – sign in the relevant equation! If it helps, label the 'observer' and 'source' on in your question on the exam paper.

Equations for the Doppler Effect of Sound (HL) (HL IB Physics)

Revision Note

The Doppler Effect of Sound

Worked example

Worked example

Examiner Tip

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M