Thermodynamic Systems (DP IB Physics): Revision Note
Change in Internal Energy
The change in the internal energy
of an ideal gas is intrinsically related to a change in its temperature
When a container containing gas molecules is heated up, the molecules begin to move around faster, increasing their kinetic energy
In a solid, where the molecules are tightly packed, molecules begin to vibrate more as they are heated
Molecules in liquids and solids have both kinetic and potential energy because they are close together and bound by intermolecular forces
However, the molecules in an ideal gas are assumed to have no intermolecular forces
This means they do not possess potential energy, only kinetic energy
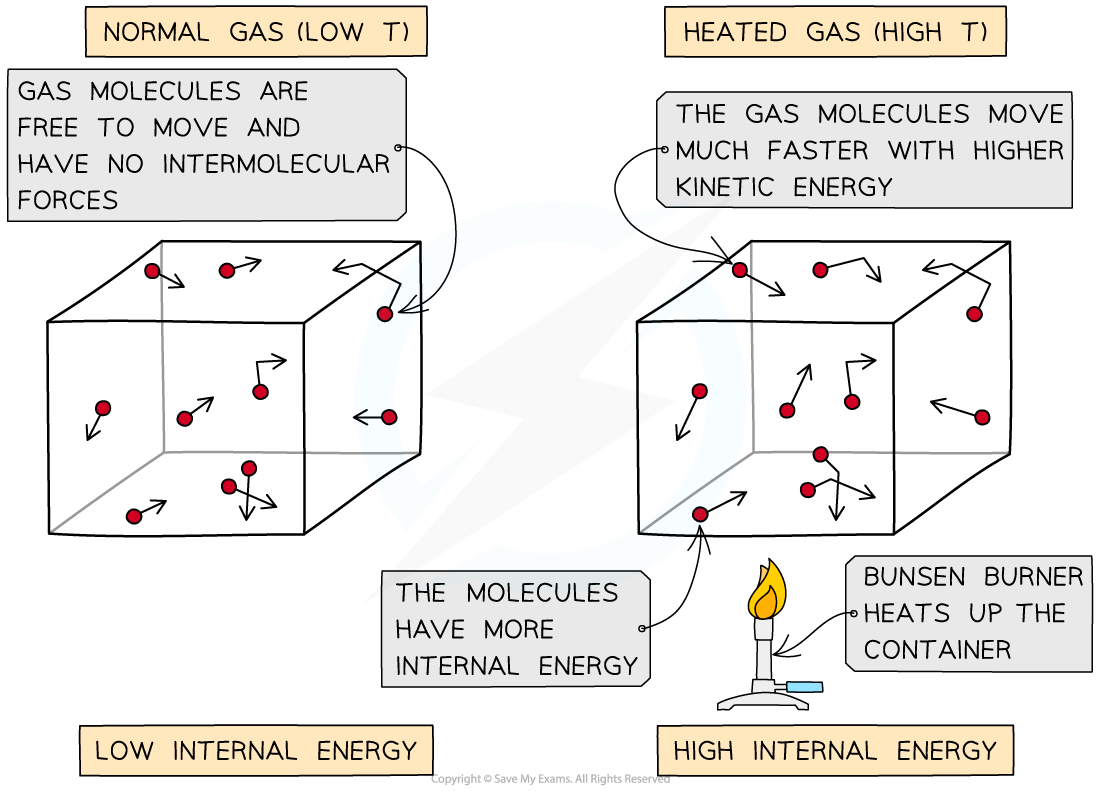
As the container is heated up, the gas molecules move faster with higher kinetic energy and therefore higher internal energy
The (change in) internal energy of an ideal gas is equal to:
Where
= change in internal energy (J)
= Boltzmann constant
= change in temperature (K)
= number of particles
Another form of this equation related to the translational kinetic energy of the particles is
Where:
= number of moles of gas (mol)
= molar gas constant
Worked Example
A student suggests that, when an ideal gas is heated from 50°C to 150°C, the internal energy of the gas is tripled.
State and explain whether the student’s suggestion is correct.
Answer:
The change in internal energy of an ideal gas is directly proportional to its change in temperature
The temperature change is the thermodynamic temperature i.e. Kelvin
The temperature change in degrees (from 50°C to 150°C) increases by three times
The temperature change in Kelvin is:
50°C + 273.15 = 323.15 K
150°C + 273.15 = 423.15 K
The temperature change, in Kelvin, does not increase by three times, therefore, neither does the internal energy
Hence, the student is incorrect
Worked Example
An ideal gas expands at constant pressure. The following data are available:
amount of gas = 126 mol
initial temperature of gas = −23.0°C
final temperature of gas = +27.0°C
Determine the change in internal energy of the gas during this expansion.
Answer:
The change in internal energy of a gas is equal to
Where
Amount of gas,
= 126 mol
Gas constant,
= 8.31 J mol−1 K−1
Change in temperature,
= 27 − (−23) = 50°C
Examiner Tips and Tricks
If an exam question about an ideal gas asks for the total internal energy, remember that this is equal to the total kinetic energy since an ideal gas has zero potential energy
Work Done by a Gas
When a gas expands, it does work on its surroundings by exerting pressure on the walls of the container it's in
For a gas inside a piston, the force exerted by the gas pushes the piston outwards
As a result, work is done on the piston by the gas
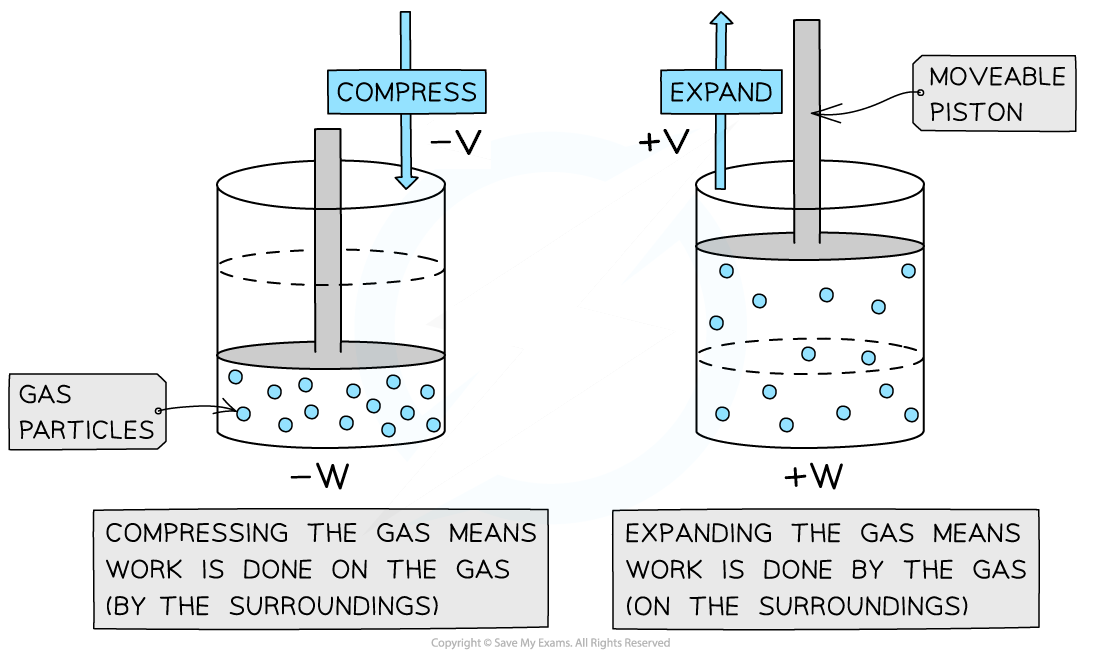
Alternatively, if an external force is applied to the piston, the gas will be compressed
In this case, work is done on the gas by the piston
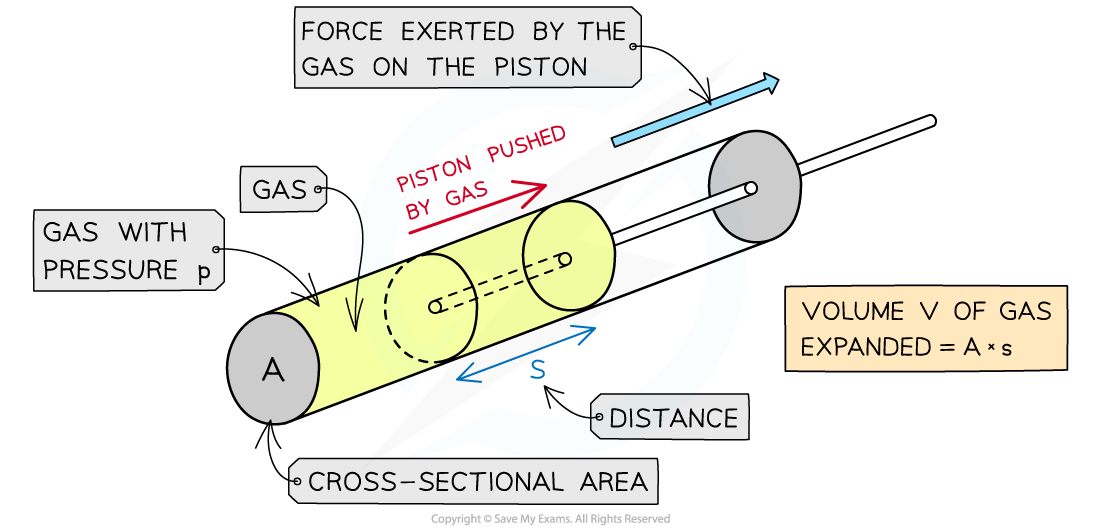
The expansion of the gas does work on the piston by exerting a force over a distance, s
Assuming the volume of gas is kept at constant pressure, this means the force F exerted by the gas on the piston is equal to:
Where A = cross-sectional area of the cylinder (m2)
The definition of work done is:
Where s = displacement in the direction of force (m)
The displacement s of the gas multiplied by the cross-sectional area A is equal to the increase in volume ΔV of the gas:
This gives the equation for the work done when the volume of a gas changes at constant pressure:
Where:
W = work done (J)
p = pressure of the gas (Pa)
ΔV = change in the volume of the gas (m3)
This equation assumes that the surrounding pressure does not change as the gas expands
This is true if the gas is expanding against the pressure of the atmosphere, which changes very slowly
p-V diagrams
Pressure-volume (p-V) diagrams are often used to represent changes in the state of a gas in thermodynamic processes
Positive or negative work done depends on whether the gas is compressed or expanded
When a gas expands (at constant pressure) work done is positive
Volume increases +ΔV
Work is done by the gas +W

When a gas is compressed (at constant pressure) work done W is negative
Volume decreases −ΔV
Work is done on the gas −W

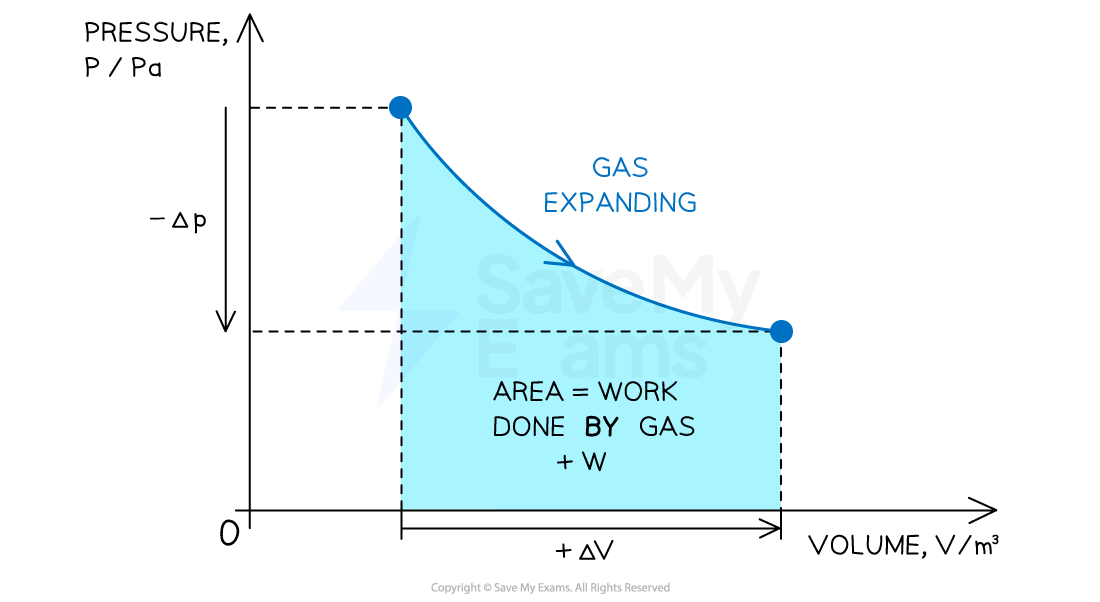
When both the volume and pressure of gas changes
The work done can be determined from the area under a p-V diagram
Worked Example
When a balloon is inflated, its rubber walls push against the air around it.
Calculate the work done when the balloon is blown up from 0.015 m3 to 0.030 m3.
Atmospheric pressure = 1.0 × 105 Pa.
Answer:
The work done by a gas is equal to
Where the change in volume is
ΔV = final volume − initial volume = 0.030 − 0.015 = 0.015 m3
Therefore, work done is
W = (1.0 × 105) × 0.015 = 1500 J
Worked Example
An ideal gas is compressed, as shown on the graph below.
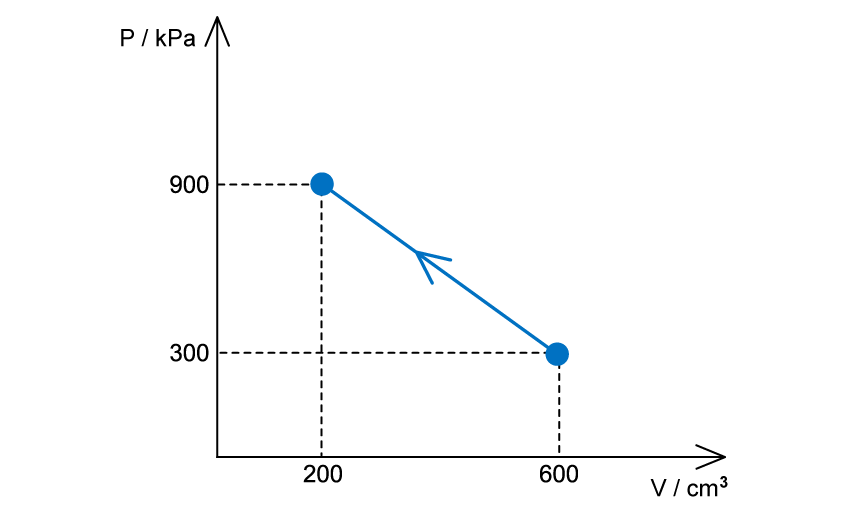
(a) For this change, state and explain whether work is done on the gas or by the gas
(b) Determine the value of the work done and state whether it is positive or negative
Answer:
(a)
The volume decreases, therefore, work is done on the gas
(b)
The work done is equal to the area under the p-V diagram
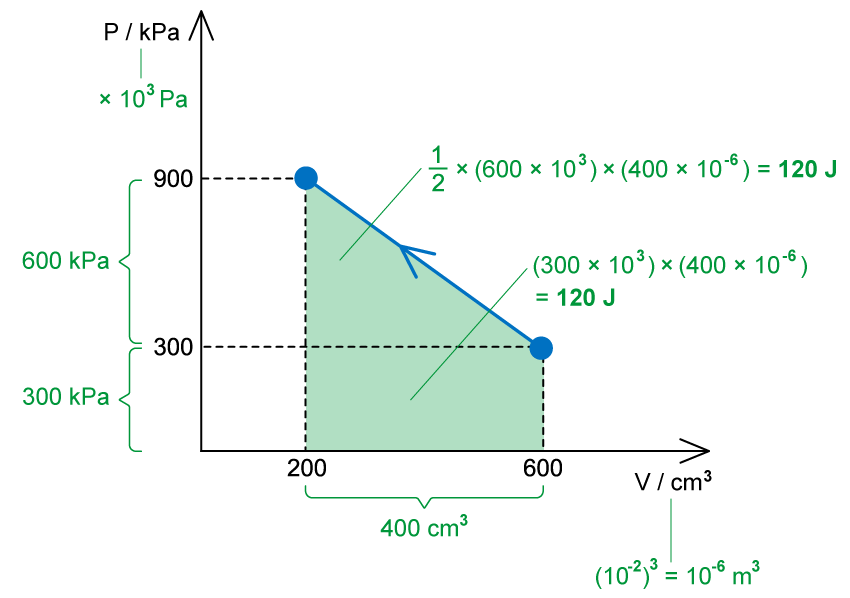
W = −240 J
When volume decreases, the work done is negative
Examiner Tips and Tricks
The pressure p in the work done by a gas equation is not the pressure of the gas but the pressure of the surroundings. This is because when a gas expands, it does work on the surroundings.

Unlock more, it's free!
Did this page help you?