The Carnot Cycle (HL) | HL IB Physics Revision Notes 2025

The Carnot Cycle

A thermodynamic system that runs at its greatest possible efficiency follows a cycle called the Carnot cycle

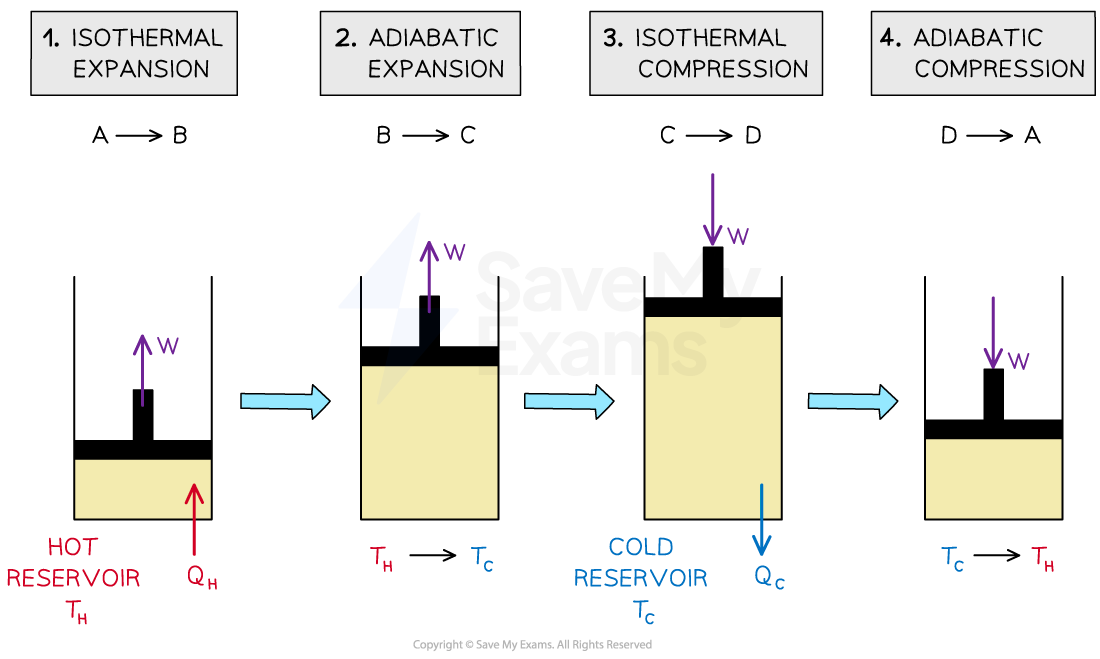
2-4-8-carnot-cycle-diagram

The four stage Carnot cycle of a gas in a piston

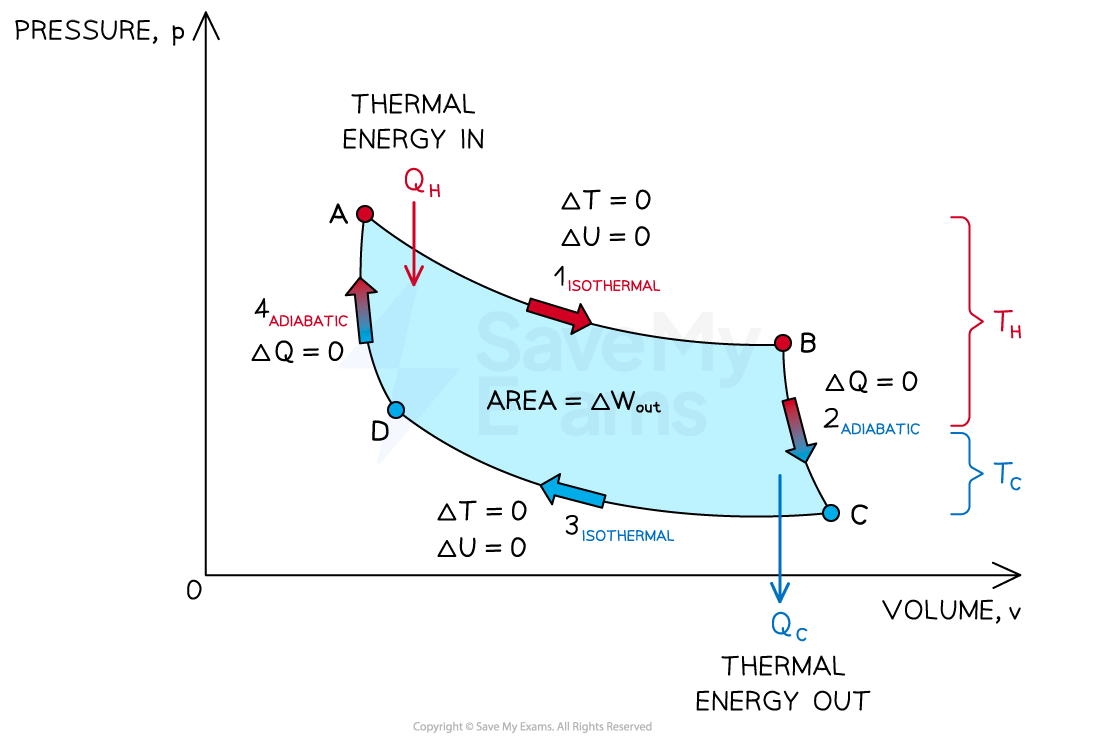
2-4-8-carnot-cycle-pv-diagram

p-V diagram for the Carnot cycle. The enclosed area equals the work done after one cycle

The Carnot cycle is an idealised and reversible process
It consists of four stages:

1. Isothermal expansion

- The gas absorbs heat $Q_{H}$ from a hot reservoir at temperature $T_{H}$
- Work is done by the gas as it expands i.e. volume increases, temperature is constant $(∆ T = 0)$
- Work done by the gas = heat gained $Q_{H}$

2. Adiabatic expansion

- The gas continues to expand
- The gas does work on the surroundings as its volume increases and pressure decreases
- The gas cools down from $T_{H}$ to $T_{C}$ , but no thermal energy is transferred $(∆ Q = 0)$

3. Isothermal compression

- The gas is compressed and transfers heat $Q_{C}$ to a cold reservoir at temperature $T_{C}$
- Work is done on the gas as it is compressed i.e. volume decreases, temperature is constant $(∆ T = 0)$
- Work done on the gas = heat lost $Q_{C}$

4. Adiabatic compression

- The gas continues to be compressed
- Work is done on the gas as its volume decreases and pressure increases
- The gas heats up from $T_{C}$ to $T_{H}$ , but no thermal energy is transferred $(∆ Q = 0)$
At the end of the fourth stage, the gas has returned to its original state and the cycle can be repeated as many times as needed

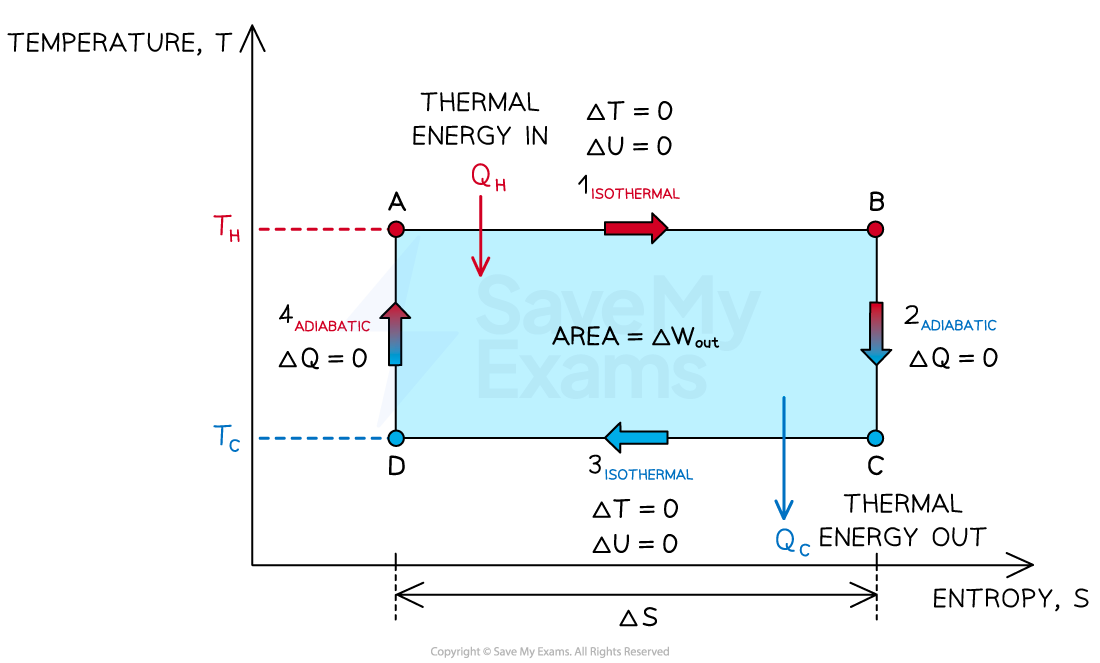
2-4-8-carnot-cycle-ts-diagram

The variation of temperature and entropy throughout the Carnot cycle

As the efficiency of a thermodynamic system increases, the difference between the temperatures of the hot and cold reservoirs increases
The maximum theoretical efficiency of a heat engine using the Carnot cycle is:

$η_{C} = 1 - \frac{T_{C}}{T_{H}}$

Where:
- $η_{C}$ = maximum theoretical efficiency (Carnot cycle only)
- $T_{C}$ = temperature in the cold reservoir (K)
- $T_{H}$ = temperature in the hot reservoir (K)

Worked example

In an idealised heat engine, the hot and cold reservoirs are held at temperatures of $T_{H}$ and $T_{C}$ respectively.

Using the equation for the change in entropy

$∆ S = \frac{∆ Q}{T}$

Show that the maximum theoretical efficiency of a heat engine is given by

$η_{C} = 1 - \frac{T_{C}}{T_{H}}$

Answer:

Step 1: Determine the change in entropy during isothermal expansion

In isothermal expansion (AB): the gas absorbs heat $Q_{H}$ from a hot reservoir at temperature $T_{H}$
Therefore, the increase in entropy is:

$∆ S_{A B} = \frac{Q_{H}}{T_{H}}$

Step 2: Determine the change in entropy during isothermal compression

In isothermal compression (CD): the gas transfers heat $Q_{C}$ to a cold reservoir at temperature $T_{C}$
Therefore, the decrease in entropy is:

$∆ S_{C D} = - \frac{Q_{C}}{T_{C}}$

Step 3: Consider the net change in entropy over the cycle

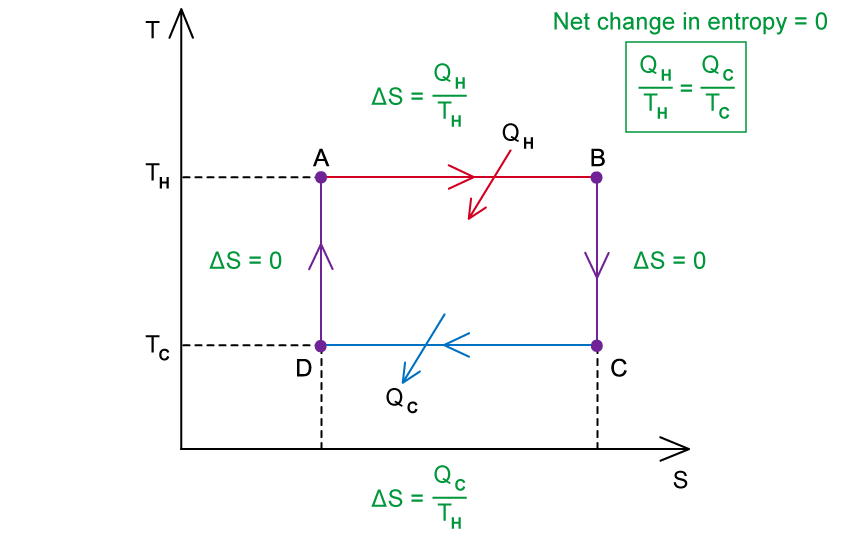
2-4-8-carnot-cycle-entropy-worked-example-ma

During adiabatic expansion (BC) and compression (DA), entropy does not change as there is no thermal energy gained or lost

$∆ S_{B C} = ∆ S_{D A} = 0$

We know that the overall entropy of the system does not change in a cyclic process, therefore

$∆ S = ∆ S_{A B} + ∆ S_{B C} + ∆ S_{C D} + ∆ S_{D A}$

$∆ S = \frac{Q_{H}}{T_{H}} + 0 + (- \frac{Q_{C}}{T_{C}}) + 0 = 0$

$\frac{Q_{H}}{T_{H}} = \frac{Q_{C}}{T_{C}} \Rightarrow \frac{Q_{C}}{Q_{H}} = \frac{T_{C}}{T_{H}}$

Step 4: Substitute the expression into the equation for the efficiency of a heat engine

The efficiency of a heat engine is given by:

$η = \frac{u s e f u l w o r k}{i n p u t e n e r g y} = \frac{W}{Q_{H}}$

Where useful work is $W = Q_{H} - Q_{C}$

$η = \frac{Q_{H} - Q_{C}}{Q_{H}} = 1 - \frac{Q_{C}}{Q_{H}}$

Combining with the expression derived above gives:

$η_{C} = 1 - \frac{T_{C}}{T_{H}}$

Worked example

An engineer designs a heat engine that has an inlet temperature of 500 K and an outlet temperature of 300 K. The engineer claims that 100 kJ of thermal energy flows out of the hot reservoir and 25 kJ of thermal energy flows into the cold reservoir.

Determine, with reference to the second law of thermodynamics, whether this engine is thermodynamically possible.

Answer:

Step 1: Determine the efficiency of the proposed engine

The efficiency of this engine would be

$η = \frac{W}{Q_{H}} = \frac{Q_{H} - Q_{C}}{Q_{H}} = 1 - \frac{Q_{C}}{Q_{H}}$

Where:
- Heat transferred in, $Q_{H}$ = 100 kJ
- Heat transferred out, $Q_{C}$ = 25 kJ

Efficiency = $1 - \frac{25}{100}$ = 0.75 = 75%

Step 2: Determine the maximum theoretical (Carnot) efficiency of the proposed engine

A Carnot engine operating between the same temperatures would have an efficiency of

$η_{C} = 1 - \frac{T_{C}}{T_{H}}$

Where:
- Inlet temperature, $T_{H}$ = 500 K
- Outlet temperature, $T_{C}$ = 300 K

Carnot efficiency: $η_{C} = 1 - \frac{300}{500}$ = 0.4 = 40%

Step 3: Discuss the proposed engine in relation to the second law

The Clausius form of the second law states: it is impossible for heat to flow from a cooler body to a hotter body without performing work
This law sets an upper limit on the maximum possible efficiency of the transfer of thermal energy to mechanical energy in a heat engine
The maximum possible efficiency of the proposed engine is 40%, but the engineer is proposing an efficiency of 75% i.e. an efficiency greater than the Carnot efficiency
This violates the Clausius form of the second law, hence the proposed engine is impossible

The Carnot Cycle (HL) (HL IB Physics)

Revision Note

The Carnot Cycle

Worked example

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M