Calculating Changes in Entropy (HL) | HL IB Physics Revision Notes 2025

Calculating Changes in Entropy

At a constant temperature T, the change in entropy on a macroscopic level can be calculated using the equation

$∆ S = \frac{∆ Q}{T}$

Where:
- ΔS = change in entropy (J K⁻¹)
- ΔQ = heat given to or removed from the system (J)
- T = temperature of the system (K)

When heat is given to a system (ΔQ = positive), entropy increases

$∆ S = + \frac{∆ Q}{T}$

$∆ Q > 0$

$∆ S > 0$

When heat is removed from a system (ΔQ = negative), entropy decreases

$∆ S = - \frac{∆ Q}{T}$

$∆ Q < 0$

$∆ S < 0$

For a reversible process that returns the system to its original state, entropy is constant

$∆ Q = 0$

$∆ S = 0$

Entropy & Microstates

The entropy of a system, on a microscopic level, can be calculated using the equation

$S = k_{B} \ln Ω$

Where:
- S = entropy of a system of microscopic particles (J K⁻¹)
- k_B = the Boltzmann constant
- Ω = the number of possible microstates of the system

Similarly, the change in entropy when the number of microstates increases from $Ω_{1}$ to $Ω_{2}$ is given by

$∆ S = k_{B} \ln \frac{Ω_{2}}{Ω_{1}}$

A microstate describes one state or possible arrangement of the particles in the system
- A state can be defined by any microscopic or macroscopic property that is known about the system e.g. positions or velocities of molecules, energy, volume etc.

An example that helps illustrate this is a two-compartment container which holds N distinguishable particles (i.e. each particle can be identified individually)
Initially, all N particles are sealed in one of two compartments

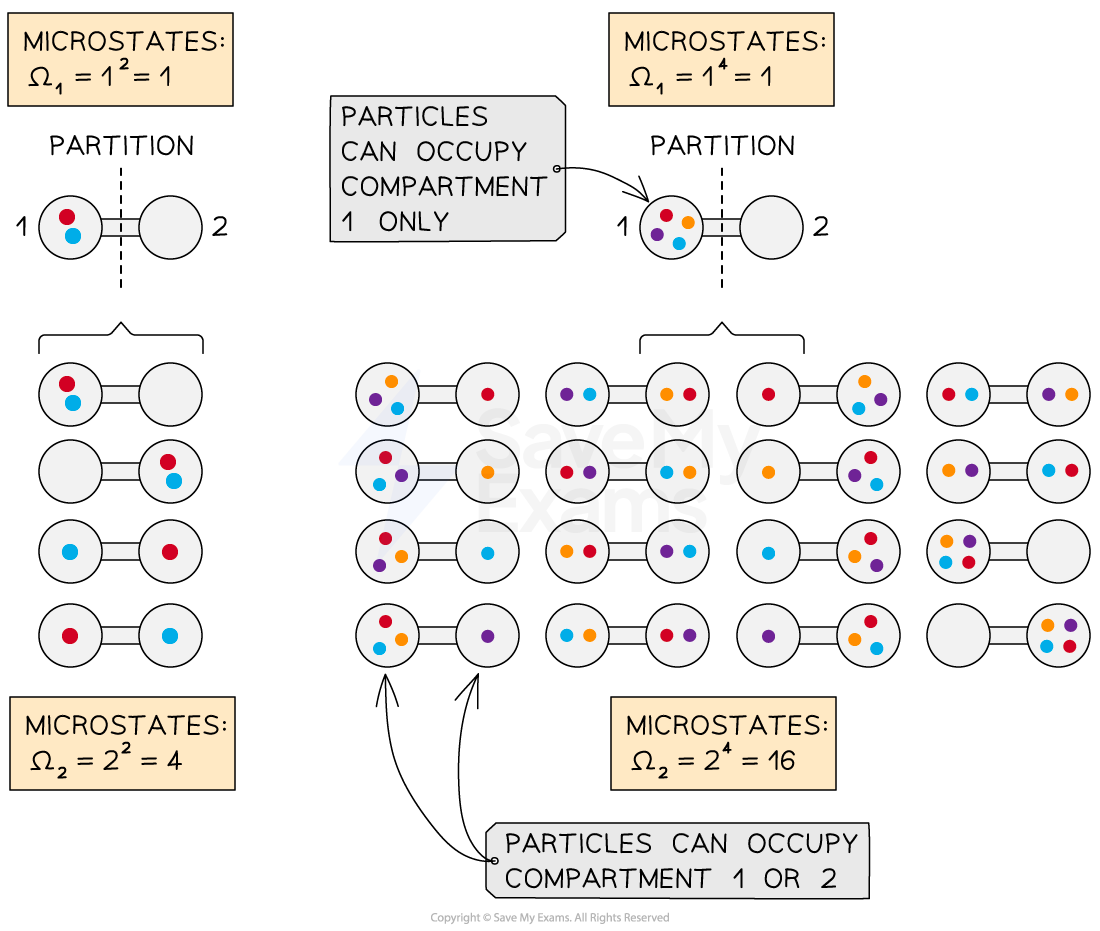
2-4-4-entropy-microstates-example

The number of possible microstates describes the number of different possible arrangements of particles in a system

When the particles are confined to one compartment, we know the location of all the particles
- Therefore, the number of microstates (possible arrangements) in the initial volume is $Ω_{1} = 1^{N} = 1$
- It is always equal to 1, for example, when N = 2 or N = 4: $Ω_{1} = 1^{2} = 1^{4} = 1$

Once the partition is removed, the particles can spread out and occupy either one of the two compartments
- The number of microstates (possible arrangements) in the final volume is $Ω_{2} = 2^{N}$
- For example, when N = 2, the particles can be arranged 2² = 4 different ways
- Or, when N = 4, the particles can be arranged 2⁴ = 16 different ways

The change in the entropy is therefore:

$∆ S = k_{B} \ln (\frac{Ω_{2}}{Ω_{1}}) = k_{B} \ln (\frac{2^{N}}{1^{N}})$

$∆ S = k_{B} \ln (2^{N})$

It follows that the number of possible microstates can be equated to macroscopic properties of the gas, such as its volume increasing from V to 2V
As the gas expands, the space it can occupy doubles, hence it gains an amount of entropy equal to:

$∆ S = N k_{B} \ln (2 V) - N k_{B} \ln (V)$

$∆ S = N k_{B} \ln (\frac{2 V}{V}) = N k_{B} \ln (2)$

This gives the same result as above:

$∆ S = k_{B} \ln (2^{N})$

Examiner Tip

Entropy is an incredibly important topic in physics and underpins many fundamental ideas from quantum mechanics to the determination of the Schwarzchild radius of a black hole, so don't worry if you feel a bit lost at first as it is quite a challenging concept to get your head around initially!

You might find it useful to think of microstates as a way of quantifying the certainty of information we have about the system

For example:

A solid has lower entropy than a gas because we can be more certain about the location of the atoms in the solid
A gas at a higher temperature (or pressure or volume) has a higher entropy than a similar gas at a lower temperature (or pressure or volume) because we become less certain about the location of the atoms by further increasing the possible locations they could occupy

Calculating Changes in Entropy (HL) (HL IB Physics)

Revision Note