IBPhysicsHLRevision NotesThe Particulate Nature of MatterThermal Energy TransfersSpecific Latent Heat

Syllabus Edition

First teaching 2023

First exams 2025

|

Specific Latent Heat (HL IB Physics)

Revision Note

Test yourselfFlashcards
Katie M

Author

Katie M

Last updated

Specific Latent Heat

  • During a phase change (i.e. a change of state) thermal energy is transferred to a substance or removed from it
    • During a phase change, the temperature of the substance does not change
  • In this case, the thermal energy is calculated as follows:

Q space equals space m L

  • Where:
    • Q = heat energy transferred (J)
    • m = mass of the substance in kilograms (kg)
    • L = specific latent heat of the substance (J kg–1)
  • The specific latent heat of a substance is defined as:

The amount of energy required to change the state of 1 kg of a substance without changing its temperature

  • This definition can be explained when the above equation is rearranged for L:

L space equals space Q over m

  • This means that the higher the specific latent heat of a substance, the greater the energy needed to change its state
    • Note that the specific latent heat is measured in J kg–1
  • The amount of energy required to melt (or solidify) a substance is not the same as the amount of energy required to evaporate (or condense) the same substance
  • Hence, there are two types of specific heat:
    • Specific latent heat of fusion, Lf
    • Specific latent heat of vaporisation, Lv

Specific Latent Heat of Fusion

  • Specific latent heat of fusion is defined as:

The energy released when 1 kg of liquid freezes to become solid at constant temperature
OR
The energy absorbed when 1 kg of solid melts to become liquid at constant temperature

  • This is because fusion applies to the following phase changes:
    • Solid to liquid
    • Liquid to solid

Specific Latent Heat of Vaporisation

  • Specific latent heat of vaporisation is defined as:

The energy released when 1 kg of gas condenses to become liquid at constant temperature
OR
The energy absorbed when 1 kg of liquid evaporates to become gas at constant temperature

  • This is because vaporisation applies to the following phase changes:
    • Liquid to gas
    • Gas to liquid

What is the difference between the latent heat of vaporisation and fusion?

  • For a given substance, the value of the specific latent heat of vaporisation is always higher than the value of the specific latent heat of fusion
    • In other words, Lv > Lf
  • This means more energy is required to evaporate (or condense) a substance than is needed to melt it (or solidify it)
  • During melting (fusion):
    • The intermolecular forces of attraction only need to be partially overcome to turn from a solid to a liquid
  • During evaporation (vaporisation):
    • The intermolecular forces of attraction need to be completely overcome to turn from liquid to gas
    • This requires a lot more energy

Substance Specific Latent Heat of Fusion (J kg−1) Specific Latent Heat of Vaporisation (J kg−1)
Water 4.0 × 105 1.1 × 107
Aluminium 3.3 × 105 2.3 × 106
Copper 2.1 × 105 4.7 × 106
Gold 6.3 × 104 1.7 × 106

Worked example

Determine the energy needed to melt 200 g of ice at 0°C.

  • The specific latent heat of fusion of water is 3.3 × 105 J kg–1
  • The specific latent heat of vaporisation of water is 2.3 × 106 J kg–1

Answer:

Step 1: Determine whether to use latent heat of fusion or vaporisation

  • We need to use the specific latent heat of fusion because the phase change occurring is from solid to liquid

Step 2: List the known quantities

  • Mass of the ice, m = 200 g = 0.2 kg
  • Specific latent heat of fusion of water, Lf = 3.3 × 105 J kg–1

Step 3: Write down the equation for the latent heat of fusion

Q space equals space m L subscript f

Step 4: Substitute numbers into the equation 

Q = 0.2 × (3.3 × 105)

Q = 66 000 = 66 kJ

Worked example

Energy is supplied to a heater at a rate of 2500 W.

Determine the time taken, in minutes, to boil 500 ml of water at 100°C. Ignore energy losses.

  • The specific latent heat of fusion of water is 3.3 × 105 J kg–1
  • The specific latent heat of vaporisation of water is 2.3 × 106 J kg–1

Answer:

Step 1: Determine whether to use latent heat of fusion or vaporisation

  • We need to use the specific latent heat of vaporisation because the phase change occurring is from liquid to gas

Step 2: Write down the known quantities

  • Power, P = 2500 W
  • Mass, m = 500 ml = 0.5 kg (since1 litre = 1 kg)
  • Specific latent heat of vaporisation of water, Lv = 2.3 × 106 J kg–1

Step 3: Recall the equations for power and latent heat of 

  • Power:  P space equals space E over t space space space space space space rightwards double arrow space space space space space E space equals space P t
  • Thermal energy:  Q space equals space m L subscript v

Step 4: Equate the two expressions for energy

P t space equals space m L subscript v

Step 5: Rearrange for the time t and substitute in the values

t space equals space fraction numerator m L subscript v over denominator P end fraction

t space equals space fraction numerator 0.5 space cross times space open parentheses 2.3 cross times 10 to the power of 6 close parentheses over denominator 2500 end fraction

t = 460 s = 7.7 min

Heating & Cooling Curves

  • A heating or cooling curve shows how the temperature of a substance changes with time
  • The two main features of these curves are
    • The flat sections
    • The non-flat sections
  • The flat sections show...
    • No change in temperature over time
    • The substance is undergoing a phase change
    • The thermal energy supplied to or removed from the substance only affects the potential energy of the particles
  • The non-flat sections show...
    • Changes in temperature over time
    • The substance is heating up or cooling down
    • That the thermal energy supplied to or removed from the substance changes the average kinetic energy of the particles, hence resulting in an overall change in the temperature of the substance

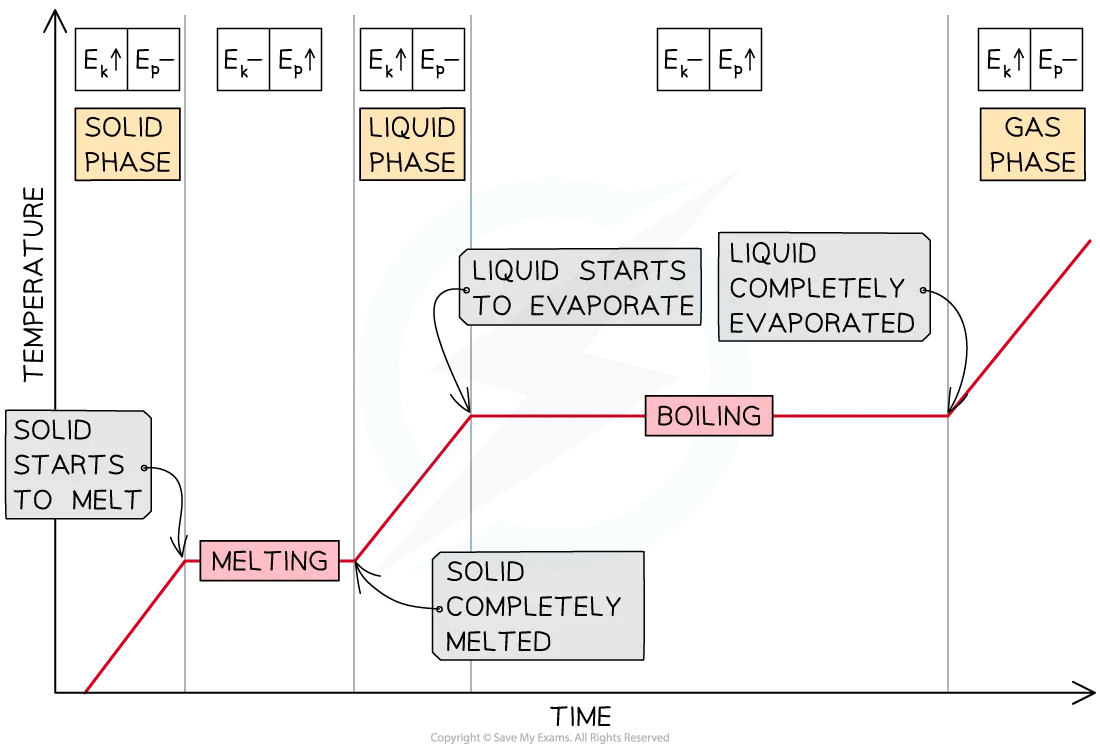
Heating Curves

  • When energy is supplied to a solid, its temperature will increase until it reaches its melting point
    • Once at the melting point, the temperature remains constant until the substance has melted completely
  • If energy continues to be supplied, the temperature of the liquid will increase until it reaches its boiling point
    • Once at the boiling point, the temperature remains constant until the substance has vaporised completely

Heating Curve of a Substance

Heating Curve of a Substance, for IB Physics Revision Notes

Cooling Curves

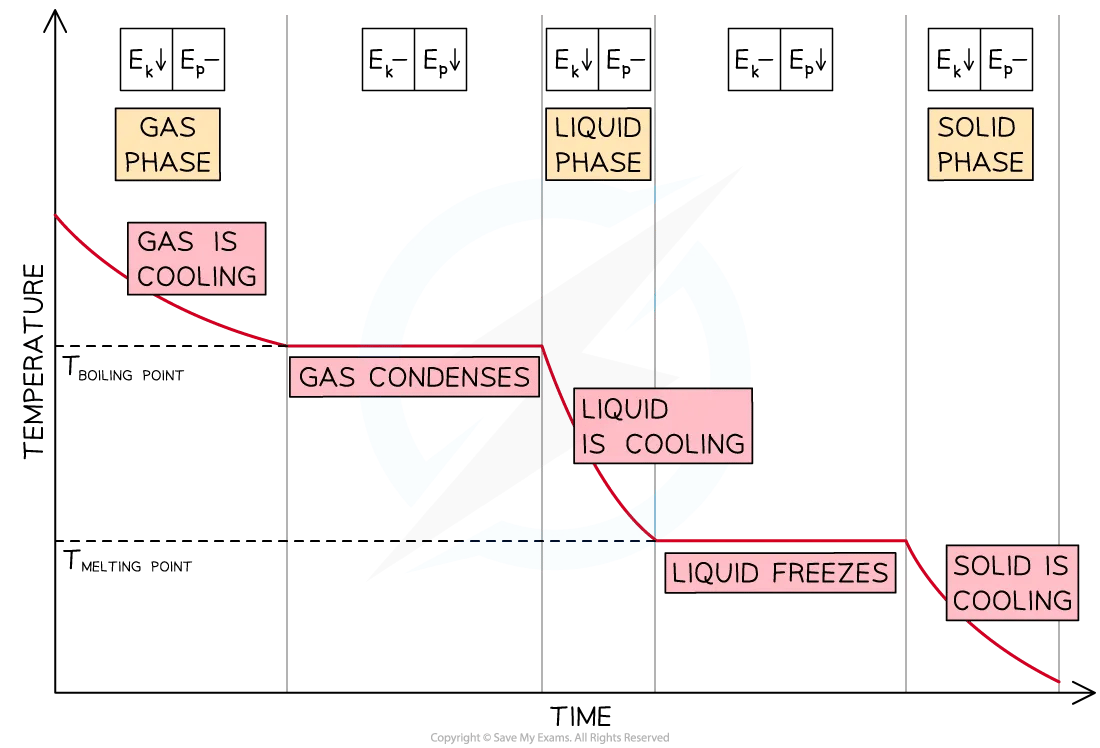
  • When energy is removed from a gas, its temperature will decrease until it reaches its boiling point
    • Once at the boiling point, the temperature remains constant until the substance has condensed completely
  • If energy continues to be removed, the temperature of the liquid will decrease until it reaches its freezing point
    • Once at the freezing point, the temperature remains constant until the substance has frozen completely

Cooling Curve of a Substance

Cooling Curve of a Substance, for IB Physics Revision Notes

  • Heating or cooling curves can also display how the temperature of a substance changes with energy
    • In the following worked example, energy (in J) is plotted on the x-axis instead of time

Worked example

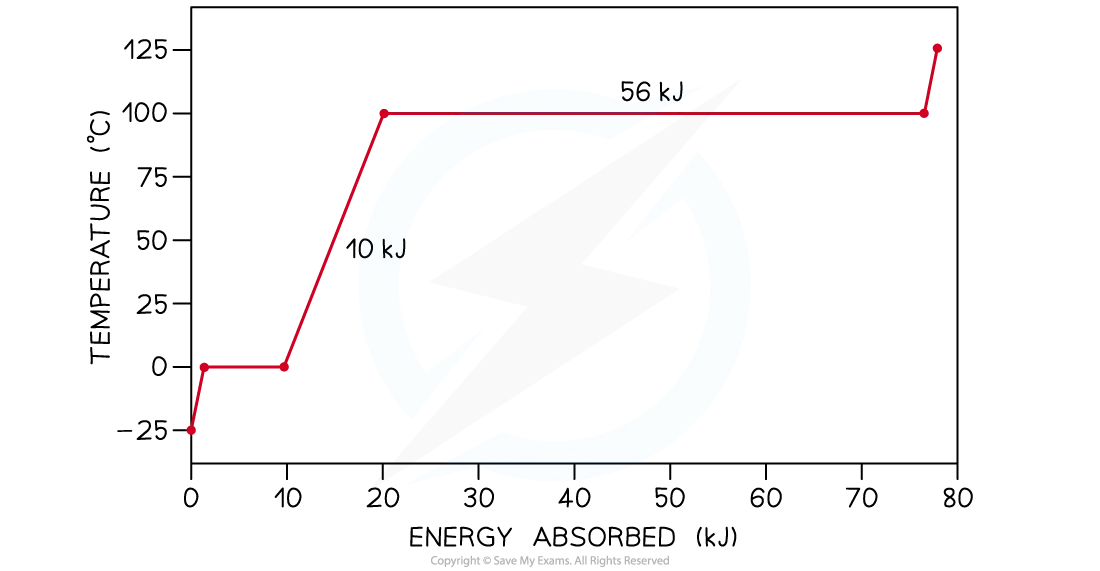
The graph below is the heating curve for a 24 g cube of ice being heated at a constant rate.

Using the graph, calculate

(a)
The specific heat capacity of water in its liquid phase
(b)
The specific latent heat of vaporisation of water
 

Specific Heat Worked Example, for IB Physics Revision Notes

Answer:

Write down the known quantities:

  • Mass of the ice, m = 24 g = 0.024 kg
  • Melting point of water = 0°C
  • Boiling point of water = 100°C
  • Change in temperature of liquid water, ΔT = 100°C

(a)

Step 1: Identify the liquid phase on the graph and read off the amount of energy absorbed

  • The non-flat region between 0°C and 100°C represents water in its liquid phase being heated up
  • Energy absorbed by liquid water = 10 kJ = 10 000 J

Step 2: Write down the equation for specific heat capacity and rearrange for c

Q space equals space m c increment T space space space space space rightwards double arrow space space space space space c space equals space fraction numerator Q over denominator m increment T end fraction

Step 3: Substitute in the values to calculate the specific heat capacity of water c

c space equals space fraction numerator 10 space 000 over denominator 0.024 cross times 100 end fraction

c = 4167 = 4200 J kg–1 °C–1

(b)

Step 1: Identify the phase change of vaporisation on the graph and read off the amount of energy absorbed

  • The second flat section at 100°C indicates the phase change from water into steam (vaporisation)
  • Energy absorbed during vaporisation = 56 kJ = 56 000 J

Step 2: Write down the equation for specific latent heat of vaporisation and rearrange for Lv 

Q space equals space m L subscript v space space space space space rightwards double arrow space space space space space L subscript v space equals space Q over m

Step 3: Substitute in the values to calculate specific latent heat of vaporisation of water Lv

L subscript v space equals space fraction numerator 56 space 000 over denominator 0.024 end fraction

Lv = 2.3 × 106 J kg–1

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Specific Heat CapacityNext:Thermal Conduction
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.