Average Kinetic Energy of a Molecule

We think of an ideal gas as molecules that collide elastically in random motion
When the molecules collide, momentum and energy are conserved
- We assume that, when the molecules are not in contact, no forces act between them
This means they have no potential energy
- Therefore, the internal energy U of an ideal, monatomic gas is equal to its average kinetic energy if the molecules are far enough apart
The average kinetic energy, E_k for one molecule is equal to:

$E_{k} = \frac{1}{2} m v^{2} = \frac{3}{2} k_{B} T$

Where:
- E_k = average kinetic energy of one molecule (J)
- v = mean square speed of one molecule (m s^–1)
- m = mass of one molecule (kg)
- k_B = Boltzmann constant
- T = temperature of the gas (K)
A consequence of this equation is that a greater gas temperature means a greater average kinetic energy of the particles
Since the total internal energy is the total kinetic energy, the internal energy of a gas U is defined as:

$U = \frac{3}{2} N k_{B} T$

Where:
- U = internal energy (J)
- N = number of molecules

The relation to the amount of substance is:

$U = \frac{3}{2} n R T$

Where:
- n = number of moles
- R = ideal gas constant
When heat is transferred to a fixed volume of gas, the internal energy increases and hence, so does the temperature, since the equations show that

$U \propto T$

This is only relevant for monatomic gases. Examples include:
- Helium
- Neon
- Argon
A monatomic (one atom) molecule only has translational energy, whilst a diatomic (two-atom) molecule has both translational and rotational energy

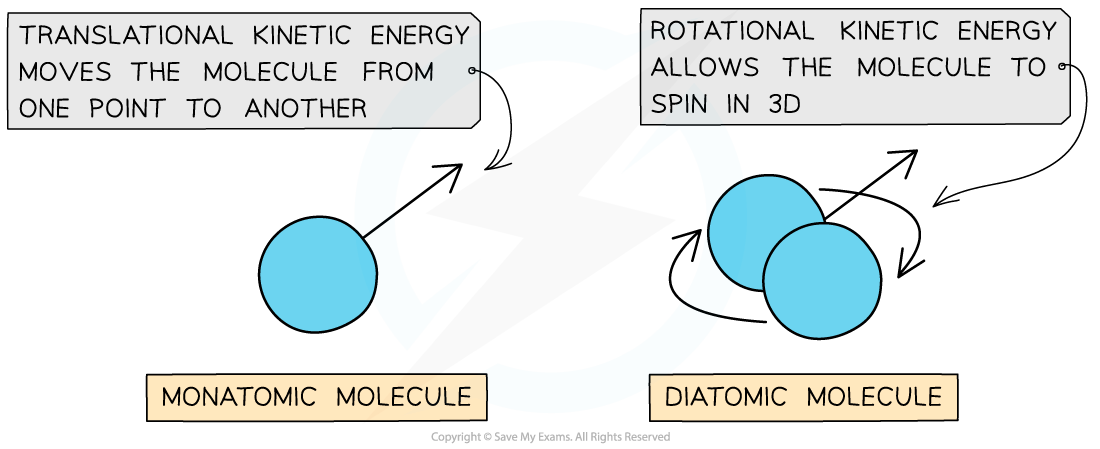
Translation and rotational KE, downloadable AS & A Level Physics revision notes

A diatomic molecule has both rotational and translational kinetic energy

Worked example

600 J of thermal energy is transferred to 3 g of helium gas kept at a constant volume in a cylinder.

Helium has a mass number of 4.

Calculate the temperature of the gas.

Answer:

Step 1: List the known quantities

Thermal (internal) energy, U = 600 J
Molar mass of helium, m_r = 4 g mol^–1 (from its mass number)
Mass of helium gas, m = 3 g

Step 2: State the relevant equation

$U = \frac{3}{2} n R T$

Step 3: Calculate the number of moles of the gas

$m_{r} = \frac{m}{n} \Rightarrow n = \frac{m}{m_{r}}$
$n = \frac{3}{4} = 0.75 moles$

Step 4: Rearrange the internal energy for the temperature, T

$T = \frac{2 U}{3 n R}$

Step 5: Substitute in the values

$T = \frac{2 \times 600}{3 \times 0.75 \times 8.31} = 64 K$

Examiner Tip

Calculations involving moles, molar mass and number of molecules are common in this topic. You should be confident with converting between these quantities for all calculations in thermal physics.

Remember the combination 'nRT' and 'Nk_BT' is also in the ideal gas equation. This shows how all the equations link together.

If you are using the equation $E_{k} = \frac{3}{2} k_{B} T$ , remember this is only for one molecule, so you will need to multiply it by the total number of molecules for a whole gas.

Average Kinetic Energy of a Molecule (HL IB Physics)

Revision Note