Angular Impulse (HL) | HL IB Physics Revision Notes 2025

Angular Impulse

In linear motion, the resultant force on a body can be defined as the rate of change of linear momentum:

$F = \frac{∆ p}{∆ t}$

An average resultant force $F$ acting for a time $∆ t$ produces a change in linear momentum $∆ p$

$∆ p = F ∆ t = ∆ (m v)$

Similarly, the resultant torque on a body can be defined as the rate of change of angular momentum:

$τ = \frac{∆ L}{∆ t}$

Where:
- $τ$ = resultant torque on a body (N m)
- $∆ L$ = change in angular momentum (kg m² s⁻¹)
- $∆ t$ = time interval (s)

An average resultant torque $τ$ acting for a time $∆ t$ produces a change in angular momentum $∆ L$

$∆ L = τ ∆ t = ∆ (I ω)$

Angular impulse is measured in kg m² s⁻¹, or N m s
This equation requires the use of a constant resultant torque
- If the resultant torque changes, then an average of the values must be used

Angular impulse describes the effect of a torque acting over a time interval
- This means a small torque acting over a long time has the same effect as a large torque acting over a short time

The area under a torque-time graph is equal to the angular impulse or the change in angular momentum

1-4-8--angular-impulse-on-a-torque-time-graph-ib-2025-physics

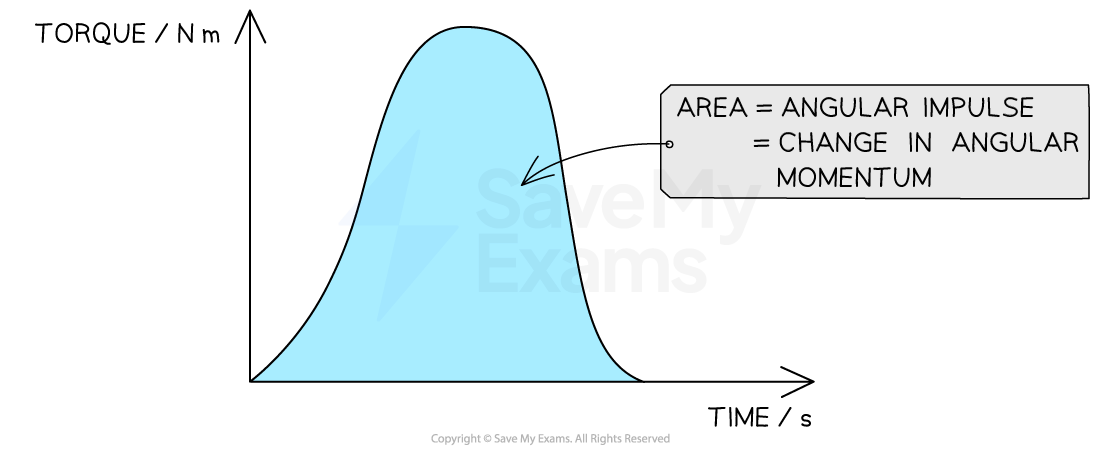
When the torque is not constant, the angular impulse is the area under a torque–time graph

The graph shows the variation of time t with the net torque $τ$ on an object which has a moment of inertia of 5.0 kg m².

1-4-8-angular-impulse-graph-worked-example-ib-2025-physics

At t = 0, the object rotates with an angular velocity of 2.0 rad s⁻¹ clockwise.

Determine the magnitude and direction of rotation of the angular velocity at t = 5 s.

In this question, take anticlockwise as the positive direction.

Answer:

Step 1: Use the graph to determine the angular impulse

The area under a torque-time graph is equal to angular impulse, or the change in angular momentum

$∆ L = τ \times ∆ t$

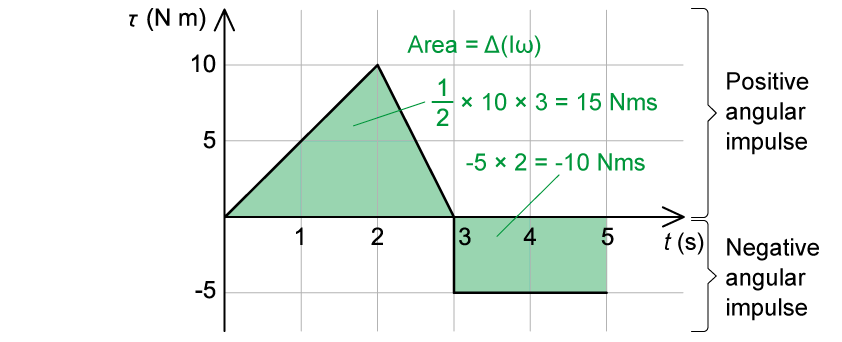
1-4-8-angular-impulse-graph-worked-example-ma-ib-2025-physics

The area under the positive curve (triangle) = $\frac{1}{2} \times 10 \times 3 = 15 N m s$
The area under the negative curve (rectangle) = $- 5 \times 2 = - 10 N m s$
Therefore, the angular impulse, or change in angular momentum is

$∆ L = 15 - 10 = 5 N m s$

Step 2: Write an expression for the change in angular momentum

$∆ L = ∆ (I ω) = I (ω_{f} - ω_{i})$

Where
- Moment of inertia, $I$ = 5.0 kg m²
- Initial angular velocity, $ω_{i}$ = −2.0 rad s⁻¹ (clockwise is the negative direction)

Step 3: Calculate the final angular velocity

$5 \times (ω_{f} - (- 2)) = 5$

$ω_{f}$ = −1.0 rad s⁻¹ in the clockwise direction