Terminal Speed (DP IB Physics): Revision Note
Terminal Speed
For a body in free fall in a vacuum, the only force acting is weight, and its acceleration g is only due to gravity
The frictional force from fluid resistance increases as the body accelerates
This increase in velocity means the viscous drag force also increases
Due to Newton’s Second Law, this means the resultant force and therefore acceleration decreases (recall F = ma)
When the viscous drag force is equal to the weight on the body, the body will no longer accelerate and will fall at a constant velocity
This velocity is called the terminal velocity
Terminal velocity can occur for objects falling through a gas or a liquid
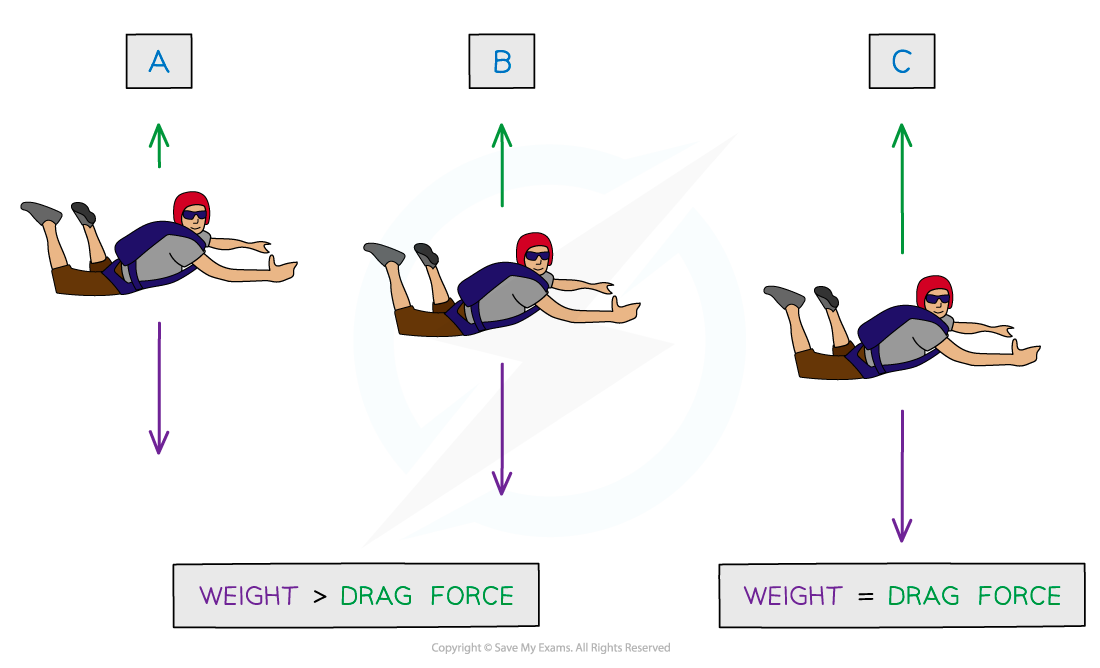
A skydiver in freefall reaching terminal velocity
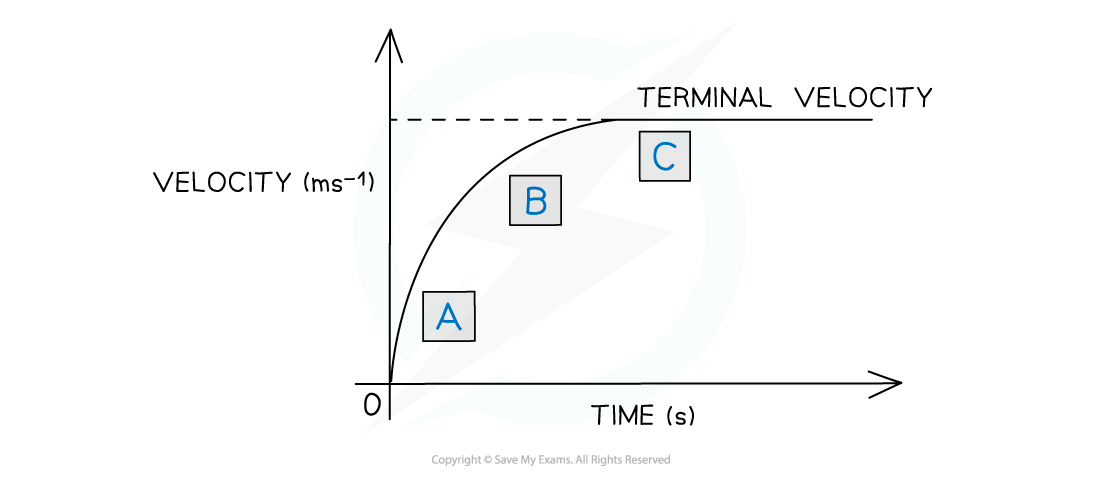
The graph shows how the velocity of the skydiver varies with time
Since acceleration is equal to the gradient of a velocity-time graph, it can be seen that
the acceleration decreases
the acceleration eventually becomes zero when terminal velocity is reached
After the skydiver deploys their parachute, they decelerate to a lower terminal velocity to reduce the impact on landing
This is demonstrated by the graph below:
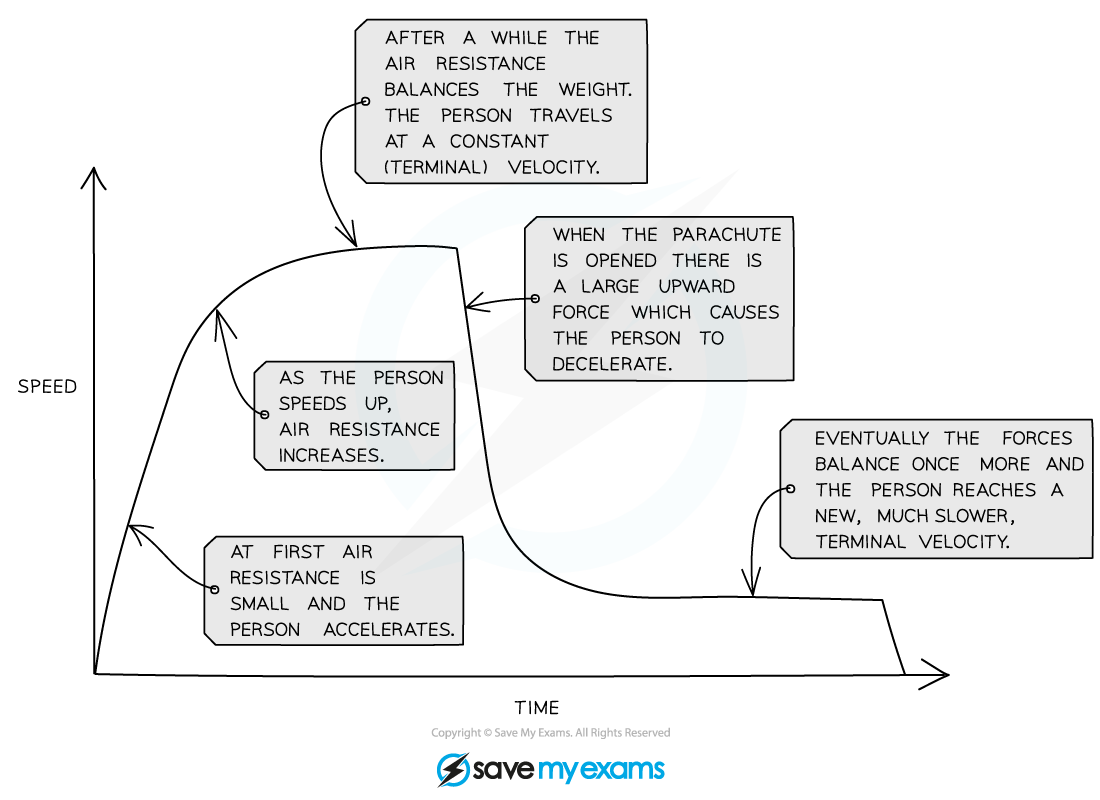
A graph showing the changes in speed of the skydiver throughout their entire journey in freefall
Worked Example
Skydivers jump out of a plane at intervals of a few seconds.
Skydivers A and B want to join up as they fall.

Skydiver A is heavier than Skydiver B, and both skydivers can be assumed to have the same surface area and volume.
If the two skydivers want to reach terminal velocity at the same time, who should jump first?
Answer:
Step 1: Recall the factors that affect terminal velocity during free fall:
Weight: the heavier the person, the greater the weight acting on them
Therefore, a heavier person will reach a higher terminal velocity
Drag: the heavier the person, the greater the drag force required to balance the extra weight
Therefore, a heavier person will reach terminal velocity faster
Step 2: Determine which skydiver will reach a higher terminal velocity
Skydiver A has a greater mass (and weight), so he will reach a higher terminal velocity (than B)
Skydiver B has a lower mass (and weight), so he will reach a lower terminal velocity (than A)
Step 3: Determine which skydiver will reach terminal velocity first
The acceleration due to gravity is initially the same for both skydivers
However, the drag force increases at a faster rate for the heavier skydiver (A), hence they will reach terminal velocity first
Step 4: Determine which skydiver should jump first
Skydiver B should jump first since he will take longer to reach terminal velocity
This is because skydiver A has a higher mass, and hence, weight
More weight means a greater speed, therefore, A will reach terminal velocity faster than B
Examiner Tips and Tricks
A common misconception is that skydivers move upwards when their parachutes are deployed - however, this is not the case, they are in fact decelerating to a lower terminal velocity.
If a question considers air resistance to be ‘negligible’ this means in that question, air resistance is taken to be so small it will not make a difference to the motion of the body. You can take this to mean there are no drag forces acting on the body.

Unlock more, it's free!
Did this page help you?