Syllabus Edition

First teaching 2023

First exams 2025

Space-Time Interval (HL) (HL IB Physics)

Revision Note

Test yourself Flashcards

Author

Ashika

Last updated

16 July 2024

Space-Time Interval

Einstein discovered that time and distance changes when moving from one inertial reference frame to another when travelling at speeds close to the speed of light
- In other words, these reference frames are not absolute

However, some quantities are the same in all inertial frames. These are called invariant
These are:
- Proper time, t₀
- Proper length, L₀
- Space-time interval, Δs

These are a product of Einstein's second postulate
In Galilean relativity:
- Space and time are the same in all reference frames, i.e. $Δ t = Δ t'$ and $Δ x = Δ x'$

In special relativity:
- These are replaced with a space-time interval, as space and time are connected together as 4 coordinates (x, y, z, t) for an event
- Motion can be represented as spanning both space and time using this coordinate system

The diagram below shows a person moving in both space x and z and in time t
- They can also move in the y direction, but 4 dimensions are not possible to draw accurately here (in 3-dimensional space)

1-5-10-space-time-interval Motion in space-time. The length of the arrow for the space-time interval is the same for all inertial reference frames

An interval in space-time is an invariant quantity in all inertial reference frames and is defined as:

${(Δ s)}^{2} = {(c Δ t)}^{2} - {(Δ x)}^{2}$

Where:
- $Δ t$ = time interval / separation (s)
- $c$ = the speed of light
- $Δ x$ = spacial separation (m)
- $Δ s$ = space-time interval (m)
This means that in two inertial reference frames, although $Δ t$ and $Δ x$ will be different in both frames, $Δ s$ will be the same
These will be used in space-time diagrams

Worked example

An inertial reference frame S' moves relative to S with a speed close to the speed of light. When clocks in both frames show zero the origins of the two frames coincide.

An event P has coordinates x = 2 m and ct = 0 in frame S, and x = 2.3 m in frame S'. Show that the time coordinate of event P in frame S' is –1.1 m.

Answer:

Step 1: List the known quantities:

Spacial separation in frame S, $∆ x$ = 2 m
Time separation in frame S, $c ∆ t$ = 0
Spacial separation in frame S', $∆ x'$ = 2.3 m

Step 2: Calculate the space-time interval in frame S

${(Δ s)}^{2} = {(c Δ t)}^{2} - {(Δ x)}^{2}$

${(∆ s)}^{2} = (0) - {(2)}^{2} = - 4$

Step 3: Substitute values into the space-time interval for S'

$∆ s$ is the same (invariant) in both reference frames

${(∆ s)}^{2} = {(c ∆ t')}^{2} - {(∆ x')}^{2}$

${(c ∆ t')}^{2} = {(∆ s)}^{2} + {(∆ x')}^{2}$

${(c ∆ t')}^{2} = - 4 + {(2.3)}^{2} = 1.29$

$c ∆ t' = \sqrt{1.29} = \pm 1.14$

Examiner Tip

The units still work out on both sides of the equation. Remember, $c Δ t$ is a speed × time which is a distance in metres, so is $Δ x$ so $Δ s$ is in metres.

Whether ct' in the worked example is + or – will come in later with space-time diagrams.

Proper Time & Length

In special relativity, we have found that distances and times are relative
This means the length of an object and the time interval of an event changes when observed in frames that are moving relative to that object
- More on this is explored in length contraction and time dilation
We need to define the difference mathematically between the time and lengths measured between each frame, to know which one is being referred to

What is Proper Time and Proper Length?

Proper time interval, Δt₀ is defined as:

The time interval between two events measured from within the reference frame in which the two events occur at the same place

Proper length, L₀ is defined as:

The length measured in a reference frame where the object is at rest (relative to the observer)

These can be measured either in the moving frame S' or a rest frame S
- This depends on the reference frame you are calculating the length and time from

For example, if a person in moving frame S' (e.g. on a train) measures the length of a book, they are at rest relative to the book
- They measure the distance between points x₂' and x₁'
- This is the proper length, L₀ although they are technically moving (but they don't know this - otherwise it would go against Einstein's first postulate)

However, for an observer in frame S, at rest (e.g. on a platform
- They will measure the distance between points x₂ and x₁
- This a shortened length, L

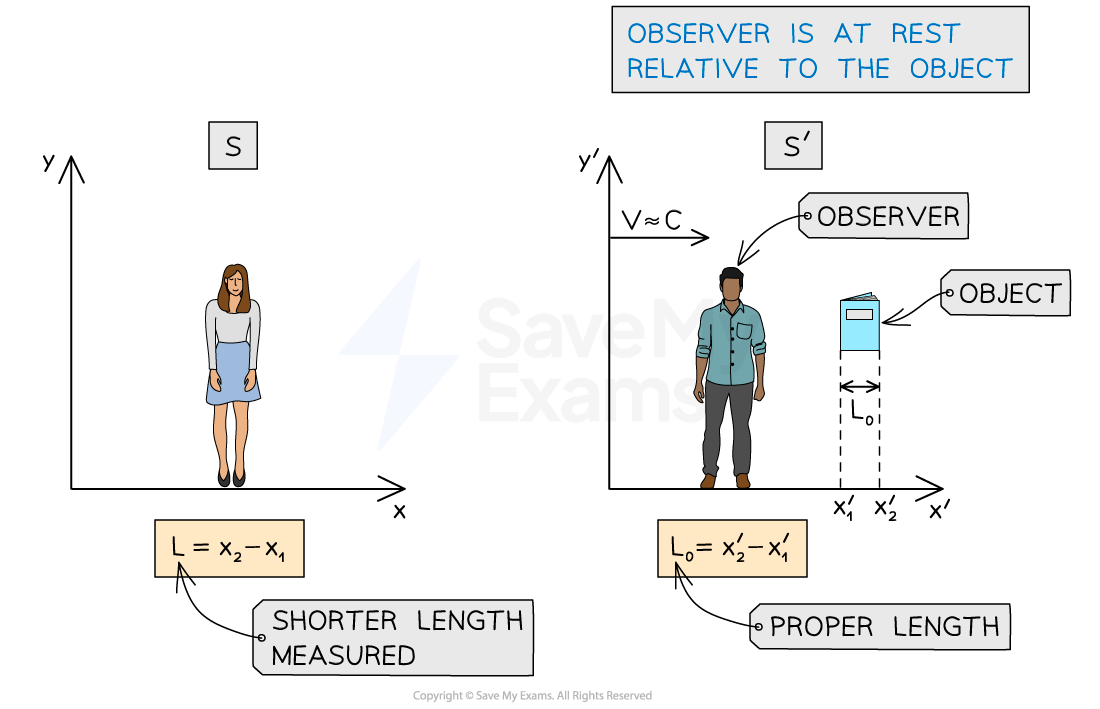
The observer in S' is measuring the proper length, because they are at rest relative to the object

For example, if a person in the stationary frame S (e.g. on the platform) measures the length of a book, they are now at rest relative to the book
- They measure the distance between points x₂ and x₁
- This is the proper length, L₀

However, an observer in frame S', which is moving (e.g. on a train) sees themselves at rest but instead sees frame S as moving (remember, motion is relative)
- They will measure the distance between points x₂' and x₁'
- This a shortened length, L

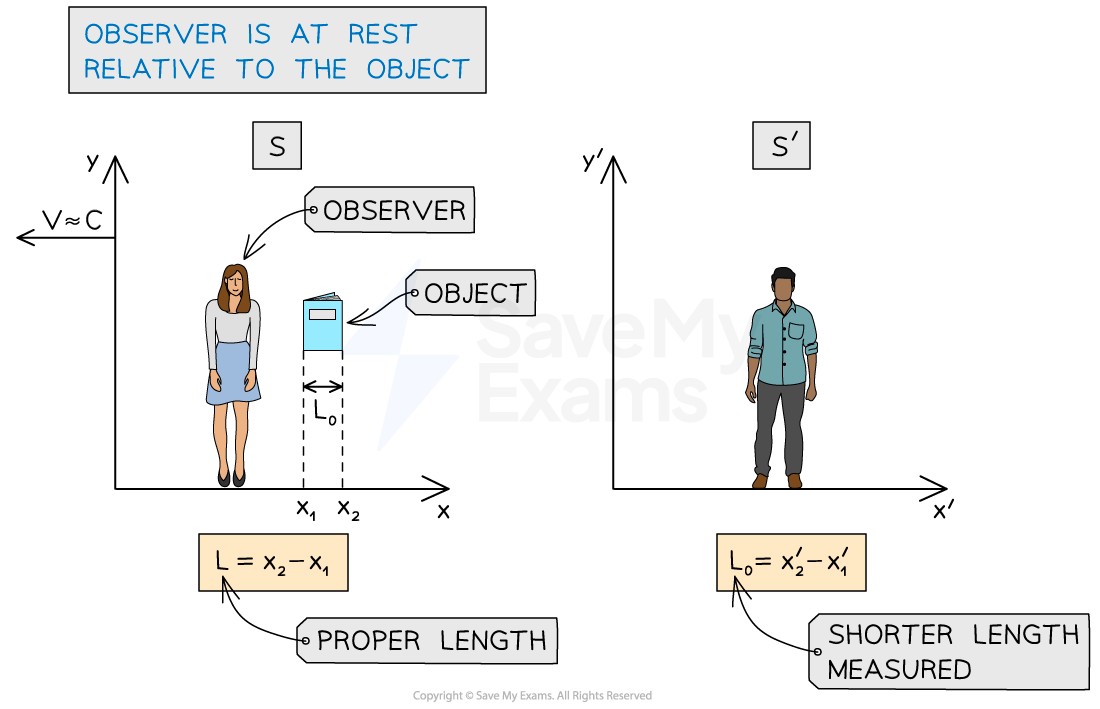
The observer in S is measuring the proper length because they are at rest relative to the object

The same rules apply for the proper time, t₀, except that the time measured from a frame moving relative to an event will be measured longer

Examiner Tip

Do not misinterpret this as the time or length measured in the stationary reference frame! This is not the case. It could be the time and length measured in the moving frame too, because it is a length and time measured by an observer at rest relative to the object

Again, this only works for objects moving close to the speed of light. You will never encounter this in everyday life!