Lorentz Transformations (HL)

Lorentz Transformation Equations

To relate measurements from one reference frame to another in Galilean relativity, we used Galilean transformations
However, Galilean transformations can no longer be used to describe distances, times and speeds for objects travelling close to the speed of light
Einstein's postulates of special relativity lead to the Lorentz transformation equations for the coordinates of an event in two inertial reference frames

The Lorentz Factor

Lorentz transformations are a correction of the Galilean transformations for speeds close to the speed of light, by multiplying by a scaling factor called the Lorentz factor, $γ$

$γ = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$

As v will always be less than c ( since nothing can travel faster than the speed of light), this means that $γ$ will always be greater than 1
This is especially important for time dilation and length contraction

Lorentz Transformation Equations

Again we have the reference frame S measuring with co-ordinates (x, y, t), and S' with co-ordinates (x', y', t')
Person F is moving away from Person E in their rocket ship at speed v which is close to the speed of light c
- Person E is a stationary observer on Earth
Both Person E and Person F witness a loud bang some distance away
- Person F measures the loud bang to be a distance x' away
- Person E measures the loud bang to be a distance x = γ(x' + vt') away

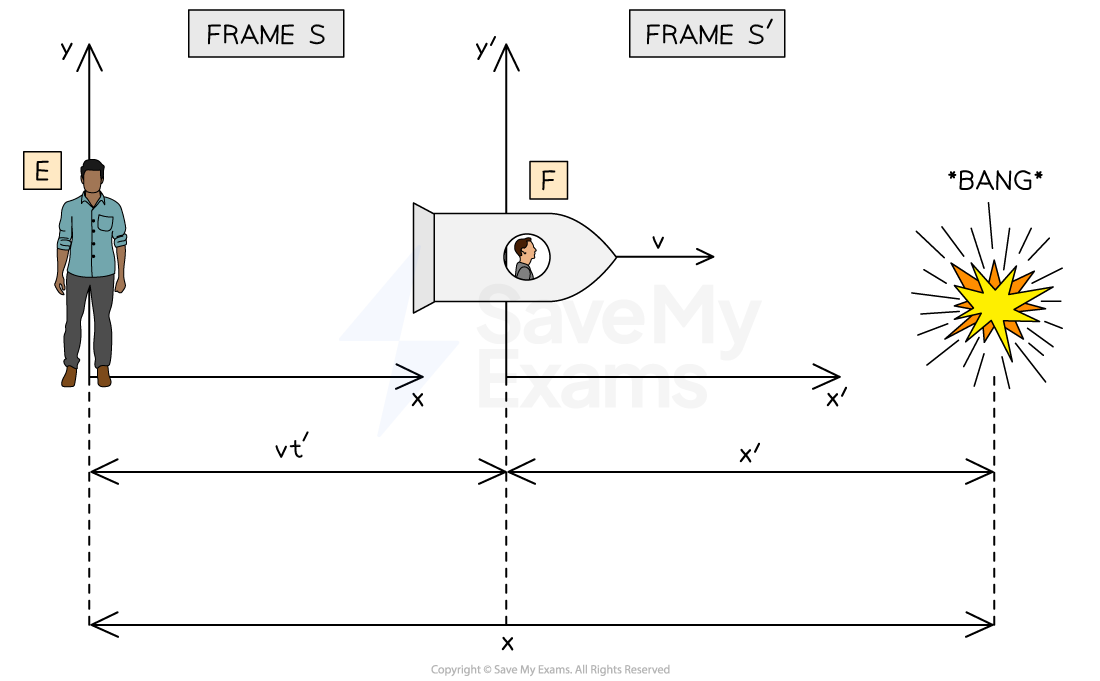
People E measures the loud bang to be at a different distance to person F

However, motion is relative
According to Person F, they are stationary and Person E is moving away from them at a velocity v in the opposite direction
So from Person F's point of view:
- Person E's velocity is -v
- Therefore, Person F measures the bang to happen at a distance x' = γ(x - vt) away
But, the time the bang happens is not the same in both frames of reference! t ≠ t'
These are the exact same equations as the Galilean transformation equations, just with the added Lorentz factor
In summary, the Lorentz equations from frame S → S' are:

$x' = γ (x - v t)$

$t' = γ (t - \frac{v x}{c^{2}})$

Where:
- (x, y, z, t) = the co-ordinates measured from one reference frame
- (x', y', z', t') = the co-ordinates measured from another reference frame moving at speed v relative to it

Galilean vs. Lorentz Transformations

Lorentz (v ≈ c)	Galilean (v << c)
$x' = γ (x - v t)$	$x' = x - v t$
$x = γ (x' + v t')$	$x = x' + v t$
$t' = γ (t - \frac{v x}{c^{2}})$	$t' = t$
$t = γ (t' + \frac{v x'}{c^{2}})$	$t = t'$
$y = y'$	$y = y'$
$z = z'$	$z = z'$

Notice that time is different between reference frames t and t' for objects travelling close to the speed of light, whilst in Galilean transformations, time was absolute (it doesn't change) between reference frames

Worked example

A rocket of proper length 150 m moves to the right with speed 0.91c relative to the ground.

1-5-5-lorentz-transformation-worked-example-ib-2025-physics

A probe is released from the back of the rocket at speed 0.45c relative to the rocket.

Determine the time it takes the probe to reach the front of the rocket according to an observer

(a)

At rest in the rocket.

(b)

At rest on the ground.

Answer:

(a)

Step 1: List the known quantities

Length of the rocket, l = 150 m
Speed of the probe, v' = 0.40c

Step 2: Analyse the situation

In the reference frame of an observer at rest in the rocket, they are stationary
Therefore, the probe travels at a constant speed 0.45c across the full length of the rocket of 150 m

$t' = \frac{l}{v'} = \frac{150}{0.45 c} = \frac{150}{0.45 \times (3 \times 10^{8})}$

$t' = 1.11 \times 10^{- 6} s$

t' and v' are used because they are the times and velocity of the moving object in the reference frame of the observer at rest

(b)

Step 1: List the known quantities

Length of the rocket, l = 150 m
Speed of the rocket, v = 0.91c
Time taken for the probe to reach the front of the rocket, t' = 1.11 × 10^–6 s

Step 2: Analyse the situation

In reference to an observer at rest on the ground, they will see the probe taking longer to reach the front of the ship
Since object in question, the probe, is moving in both reference frames, we need to use a Lorentz transformation

Step 3: Calculate the gamma factor

$γ = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} = \frac{1}{\sqrt{1 - \frac{{(0.91 c)}^{2}}{c^{2}}}}$

$γ = \frac{1}{\sqrt{1 - 0 . 91^{2}}} = 2.412$

Step 3: Substitute values into the Lorentz transformation

Since the observer is at rest, the Lorentz equation for time t must be used

$t = γ (t' + \frac{v x'}{c^{2}})$

$t = 2.412 ((1.11 \times 10^{- 6}) + \frac{(0.91 c) (150)}{c^{2}}) = 2.412 ((1.11 \times 10^{- 6}) + \frac{(0.91) (150)}{3 \times 10^{8}})$

$t = 3.8 \times 10^{- 6} s$

Examiner Tip

Always check that your value of $γ$ is greater than 1.

You will often be given a speed v in terms of c e.g. v = 0.90c etc. When you put this value into the gamma factor, this is squared. Therefore, you do not need to put in 3.0 × 10⁸ at all into your calculator, as the c² will cancel.

E.g. $γ = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} = \frac{1}{\sqrt{1 - \frac{{(0.90 c)}^{2}}{c^{2}}}} = \frac{1}{\sqrt{1 - \frac{{(0.90)}^{2} {(c)}^{2}}{c^{2}}}}$

$γ = \frac{1}{\sqrt{1 - \frac{{(0.90)}^{2} {(c)}^{2}}{c^{2}}}} = \frac{1}{\sqrt{1 - {(0.90)}^{2}}}$

The equations for x', t' and $γ$ are given in your data booklet, but you must remember the sign change if you want to calculate x or t (from the rest frame) instead!

Some textbooks may go further into this for your understanding, you will not be expected to derive these equations in your exam. You will only be assessed on how to use them.

Lorentz Transformations (HL) (HL IB Physics)

Revision Note

The Lorentz Factor

Lorentz Transformation Equations

Galilean vs. Lorentz Transformations

Lorentz (v ≈ c)

Galilean (v << c)

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Space, Time & Motion

Kinematics

Distance & Displacement

Speed & Velocity

Acceleration

Kinematic Equations

Motion Graphs

Projectile Motion

Fluid Resistance

Terminal Speed

Forces & Momentum

Free-Body Diagrams

Newton’s First Law

Newton’s Second Law

Newton’s Third Law

Contact Forces

Non-Contact Forces

Frictional Forces

Hooke's Law

Stoke's Law

Buoyancy

Conservation of Linear Momentum

Impulse & Momentum

Force & Momentum

Collisions & Explosions in One-Dimension

Collisions & Explosions in Two-Dimensions (HL)

Angular Velocity

Centripetal Force

Centripetal Acceleration

Non-Uniform Circular Motion

Work, Energy & Power

Principle of Conservation of Energy

Sankey Diagrams

Work Done

Kinetic Energy

Gravitational Potential Energy

Elastic Potential Energy

Conservation of Mechanical Energy

Energy & Power

Efficiency Formula

Energy Density

Rigid Body Mechanics

Torque & Couples (HL)

Rotational Equilibrium (HL)

Angular Displacement, Velocity & Acceleration (HL)

Angular Acceleration Formula (HL)

Moment of Inertia (HL)

Newton’s Second Law for Rotation (HL)

Angular Momentum (HL)

Angular Impulse (HL)

Rotational Kinetic Energy (HL)

Galilean & Special Relativity

Reference Frames (HL)

Galilean Relativity (HL)

Postulates of Special Relativity (HL)

Velocity Addition Transformations (HL)

Space-Time Interval (HL)

Time Dilation (HL)

Length Contraction (HL)

Simultaneity in Special Relativity (HL)

Space-Time Diagrams (HL)

Muon Lifetime Experiment (HL)

The Particulate Nature of Matter

Thermal Energy Transfers

Solids, Liquids & Gases

Density

Temperature Scales

Temperature & Kinetic Energy

Internal Energy