Revision NotesExam QuestionsFlashcardsTarget TestPast Papers
IBPhysicsDPHLRevision NotesSpace, Time & MotionGalilean & Special RelativityGalilean Relativity

Galilean Relativity (DP IB Physics): Revision Note

Ashika

Author

Ashika

Last updated

Newton's Postulates of Time & Space

  • We use inertial reference frames because Newton's laws of motion are the same in all of them

    • This is known as Galilean relativity

  • For example, an object in an inertial reference frame will continue moving in a straight line with constant velocity unless acted upon by a force

    • This is in accordance with Newton's first law of motion

  • This means that the same laws of Physics apply, regardless of one's frame of reference relative to another, as long as they are moving in a straight line at a constant velocity

  • An object moving with constant velocity in one reference frame will still have a constant (but different) velocity in another reference frame

  • The Cartesian coordinate system is generally used for reference frames

Cartesian co-ordinates in 3D and 2D diagram

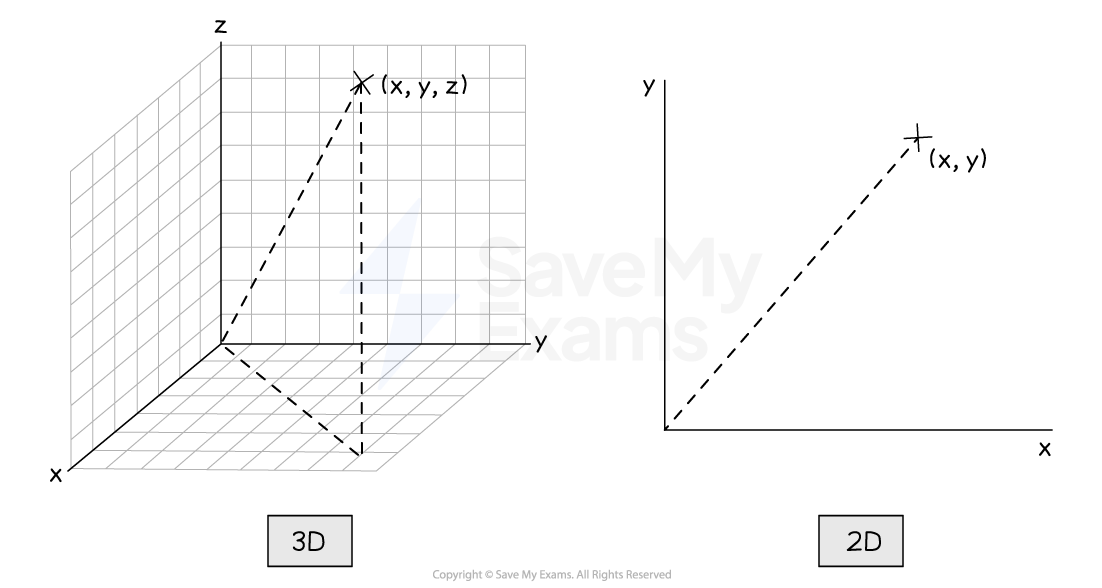
1-5-2-cartesian-co-ordinates-ib-2025-physics

Cartesian coordinates are used to represent a point in space

  • Although there are an infinite number of inertial frames of reference in the Universe, there are ways to move between them

Examiner Tips and Tricks

Remember, anything that is moving in a curved line is accelerating. Therefore, you will not come across reference frames of something moving in a circle or an arc, but only straight lines with no acceleration.

Cartesian co-ordinates are technically used to refer to a point in 3D (x, y, z), although, your exam questions will focus on movement in 2D (x, y) as this is easier to draw diagrams for.

Galilean Relativity Equations

Galilean Transformation Equations

  • Galilean transformation equations are used to convert between the coordinates of space and time of an event in one frame of reference to another

    • This is because the velocity, position and time of an event are measured differently from different reference frames

  • For example, Person D is on a skateboard travelling at 4 m s–1 when they throw a ball in a straight line at a constant velocity of 2 m s–1. Person C is a stationary observer of the event.

    • In Person D's reference frame, the ball is travelling at 2 m s–1

    • In Person C's reference frame, the ball is travelling at 4 + 2 = 6 m s–1

  • So, what is the speed of the ball? Well, it depends!

The difference in velocity of an object in two reference frames

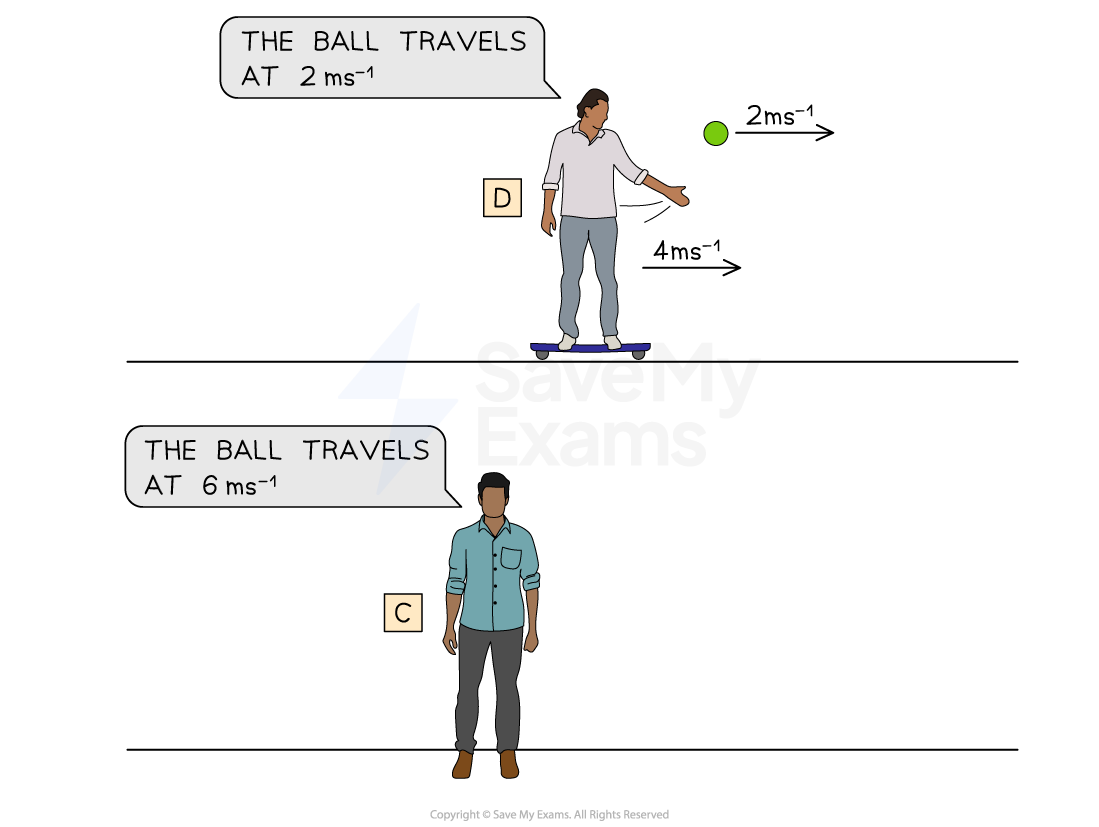
1-5-2-galilean-relativity-examples-ib-2025-physics

Person C measures the ball to be travelling faster than when measured by Person D

  • Mathematically, the position and time of an event in one reference frame, S, is represented by the coordinates (x, y, t)

  • The position and time of an event in a second reference frame, moving relative to the first one, S', is represented by the coordinates (x', y', t')

    • Remember from the train example in Reference Frames, both Person A and Person B view the other as moving because they are viewing the event from two different frames of reference

  • Now consider another example:

  • Person C is stationary whilst Person D is moving away from Person C at velocity v 

  • Both Person C and Person D witness a balloon pop at some distance away

    • Person D, in reference frame S', measures the balloon pop at a distance x' away

    • Person C, in reference frame S, measures the balloon pop at a distance x = x' + vt away

Stationary and moving reference frames

 

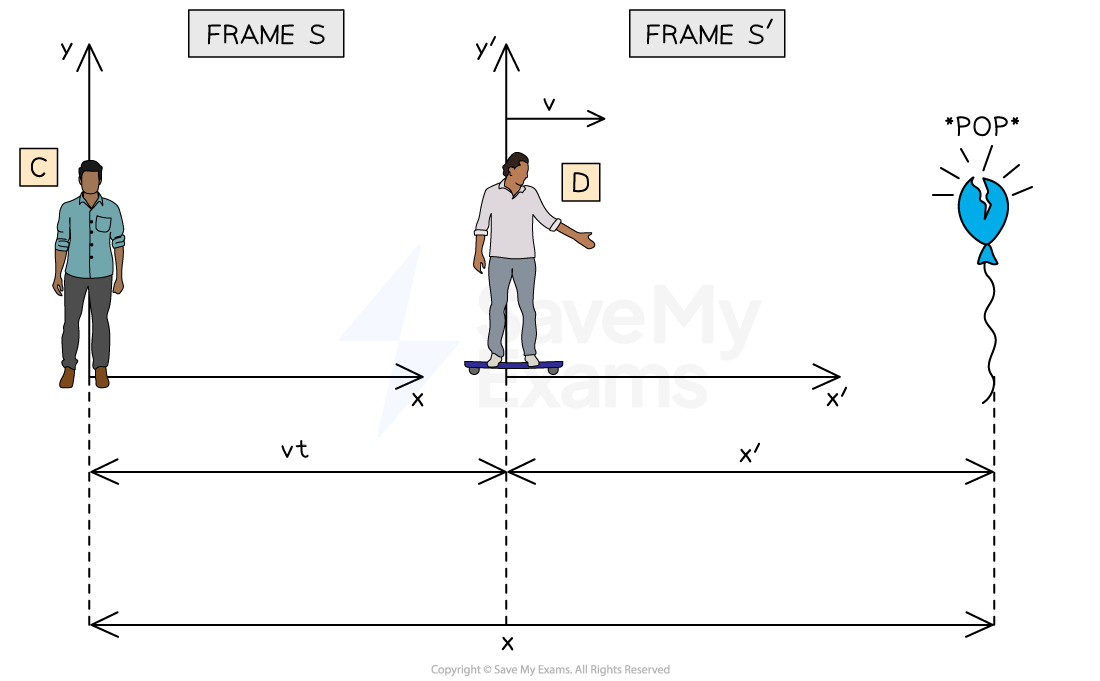
1-5-2-galilean-equations

Person C and D measure the distance at which a balloon pops differently

  • Now let's see the event from Person D's frame of reference (S')

  • From Person D's point of view, they are stationary and it is Person C that is travelling away from them at speed v

    • Since this is the opposite direction to the v observed by Person C, Person C's velocity from Person D's perspective is -v

    • Therefore, Person D measures the balloon to pop at a distance x' = x - vt away

  • Remember the vt comes from distance (x) = speed (v) × time (t). 

  • In both frames of reference, the time the balloon pops are still the same, hence t = t'

  • In summary:

Table of the Galilean relativity equations for a stationary and moving reference frame

Stationary reference frame

Moving reference frame

Transformation

x

x'

x' = x – vt

x = x' + vt

y

y'

y = y'

z

z'

z = z'

t

t'

t = t'

  • The prime notation (') always denotes the moving reference frame

    • x', y', z' u' are measurements taken from within the moving reference frame

    • x, y, z, u are measurements taken from within the stationary reference frame

  • v always refers to the velocity of the moving reference frame

  • Co-ordinates y and z, and time, t, are the same in both reference frames because the relative motion only occurs in the x direction

Worked Example

A train travels through a station at a constant velocity of 15 m s–1. One observer is sitting inside the train and another sits on the platform. As they pass each other, they start their stopwatches and watch a child on the train run at a constant speed in the same direction as the motion of the train. The observer on the train measures the speed of the child to be 2 m s–1.

(a) According to the observer on the train, how far has the child moved after 10 s?

(b) According to the observer on the platform, how far has the child moved after 10 s? 

Answer:

Draw a quick sketch of the situation

  • Label the stationary (x, t) and moving (x', t') reference frames

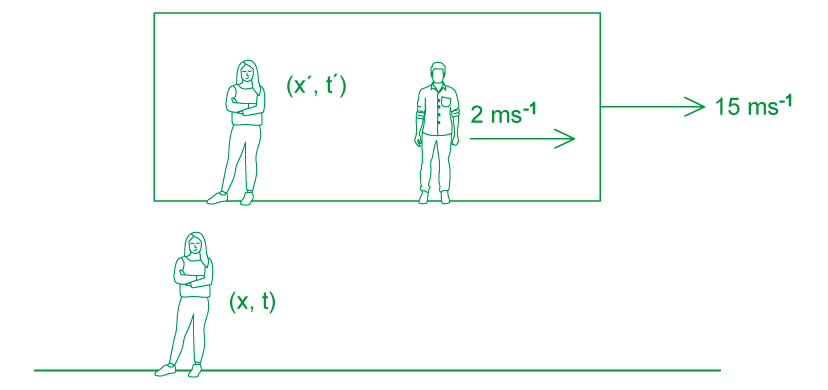
1-5-2-galilean-relativity-worked-example-solution

(a) Calculate the distance the child travels according to the observer on the train

  • The child is moving within the observer's own reference frame, so the position of the child after 10 s is x'

  • There are two velocities given:

    • v = velocity of the moving reference frame S' (the train)

    • u' = velocity of the child moving as measured from within the moving reference frame

  • The observer in S' measures the child to be travelling away at 2 m s–1

  • Since the child is moving within the observer's own reference frame, S', they can use the standard laws of physics to make the measurement

  • Therefore, using the equation

distance (x) = speed × time

  • The distance, x' is:

x' = u't

x' = 2 × 10 = 20 m

(b) Calculate the distance the child travels according to the observer on the platform

  • This observer is stationary in their reference frame, S, and is measuring an event occurring in a reference frame moving relative to theirs

  • Therefore, a Galilean transformation is required

x = x' + vt

x = 20 + (15 × 10) = 170 m

Examiner Tips and Tricks

We can explore the x' = x - vt equation, using the example above:

  • Position of child after 10 s as measured from S', x' = 20 m

  • Position of child after 10 s as measured from S, x = 170 m

  • Velocity of moving reference frame, S' (the train), v = 15 m s-1

  • Velocity of child as measured from within S', u' = 2 m s-1

x' = u't (from part (a))

x = x' + vt (from part (b))

The Galilean transformation for x' is:

x' = x - vt

Substitute in the expression (x' + vt) for x:

x' = (x' + vt) - vt

Substitute in the expression (u't) for x':

x' = (u't + vt) - vt

Simplify:

x' = u't

This is the equation we used in part (a), the velocity of the child multipled by the time.

Therefore:

x' = x - vt

x' = 170 - (15 × 10)

x' = 170 - 150 = 20 m

You do not need to perform a transformation if the measurement is taken from within the reference frame in which the evert occurs.

Note that it is always assumed that the timer in both reference frames begins, t = 0, when observer S and S' are in parallel positions.

Notice also, that you only need to remember one of the equations: x space equals space x apostrophe space plus space v t

 x apostrophe space equals space x space minus space v t is the same equation but rearranged for x' as the subject instead.

Velocity Addition Equation

  • Galilean transformations can also be used to transform velocities

    • This is known as velocity addition

Objects moving in the same direction

  • First, we will consider vector addition for objects that move in the same direction as the moving reference frame

  • Let's go back to the example of Person D on a skateboard, throwing a ball directly in front of them in a straight line

  • In this example:

    • u is the velocity of the ball as measured in frame S (by Person C)

    • u' is the velocity of the ball as measured in frame S' (by Person D)

    • v is the velocity of the moving reference frame S', Person D 

Velocity addition for two objects moving in the same direction

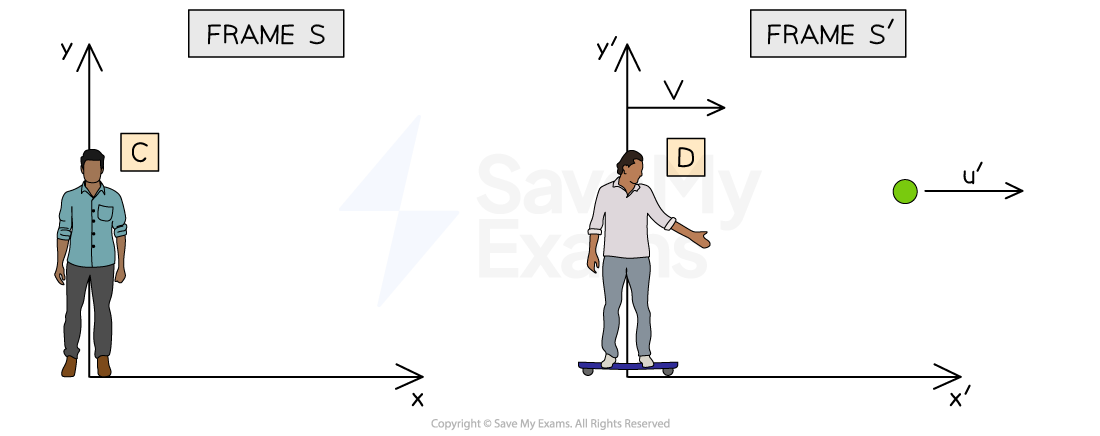
1-5-2-velocity-addition

In Person C's reference frame, the ball is travelling at a speed of u' + v

  • The ball is thrown by Person D, so the measured event (the velocity of the ball) occurs within the moving reference frame, S'

  • Therefore, Person D uses the regular laws of physics to make their measurement

    • Person D (frame S') measures the velocity of the ball to be u'

  • Because the measured event occurs in reference frame S', Person C in S must use velocity addition

    • Person C (frame S) measures the velocity of the ball to be u = v + u'

Objects moving in opposite directions

  • Velocities are vectors, so their direction must be taken into account

  • Let's say Person D now throws the ball directly behind them in a straight line at constant velocity

  • The ball is now travelling in the opposite direction to the motion of the reference frame

    • u, u' and v still refer to the same objects

  • This time, since u' is in the opposite direction to v, it is now –u'

  • Therefore:

    • Person D (frame S') measures the velocity of the ball to be –u'

    • Whilst Person C (frame S) measures the velocity of the ball to be u = v – u'

Velocity addition for two objects moving in opposite directions

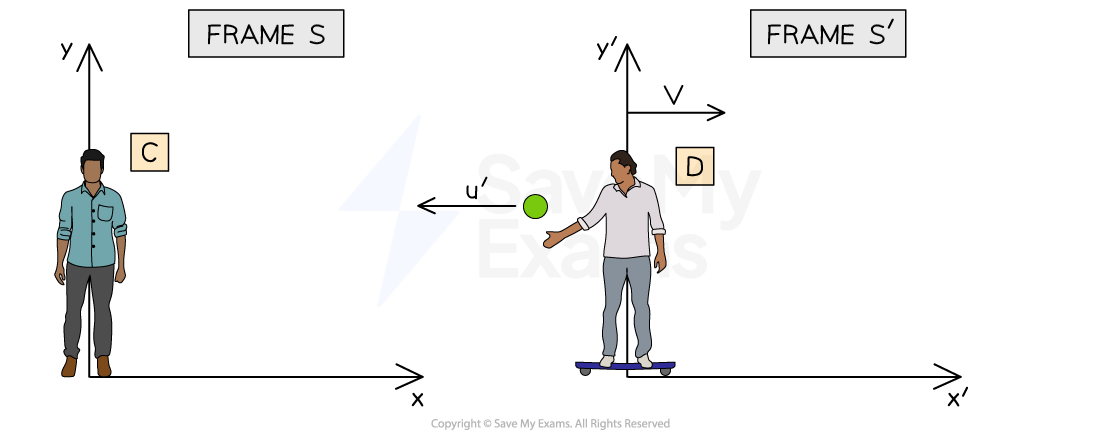
1-5-2-velocity-addition-2-ib-2025-physics

In Person C's reference frame, the ball is now travelling at a speed of v – u'

  • The velocity addition equation can be rearranged to find the transformation u' to u

u = u' + v rightwards double arrow u' = u - v

Table of the velocity addition equations for a stationary and moving reference frame

Stationary reference frame

Moving reference frame

Transformation

u

u'

u = u' + v

u' = u − v

Worked Example

Two travellers X and Y see each other at an airport. Traveller X walks at 1.5 m s-1 onto a travelator walkway that moves at 0.3 m s–1 as measured by a stationary observer. Traveller Y takes a seat facing the travelator. 

(a) Determine the velocity of Traveller X as measured by Traveller Y when Traveller X is walking in the same direction as the travelator.

(b) Determine the velocity of Traveller X as measured by Traveller Y when Traveller X is walking in the opposite direction to the travelator.

(c) Assuming Traveller X maintains this motion, determine the velocity of Traveller Y as measured by Traveller X.

(d) Assuming Traveller X still maintains this motion, Traveller Y now gets up and walks on the ground in the same direction as the motion of the travelator. Traveller Y walks at a velocity of 0.8 m s-1 relative to the ground. Determine the velocity of Traveller Y as measured by Traveller X.

Answer:

(a) Determine the velocity of Traveller X as measured by Traveller Y when Traveller X is walking in the same direction as the travelator:

List the known quantities:

  • The stationary reference frame, S = Traveller Y

  • The moving reference frame, S' = the travelerator

  • The object moving in the moving reference frame = Traveller X

  • The velocity of the moving reference frame (S'), v = 0.3 m s-1

  • The velocity of the object moving in the moving reference frame (S'), u' = 1.5 m s-1

  • The velocity of Traveller X in S' as measured by Traveller Y in S = u

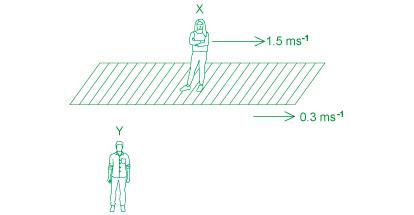
1-5-2-velocity-addition-worked-example-solution-2

Traveller Y (S) measures the velocity of Traveller X (S') to be:

u = u' + v

u = 0.3 + 1.5 = 1.8 m s-1

(b) Determine the velocity of Traveller X as measured by Traveller Y when Traveller X is walking in the opposite direction to the travelator

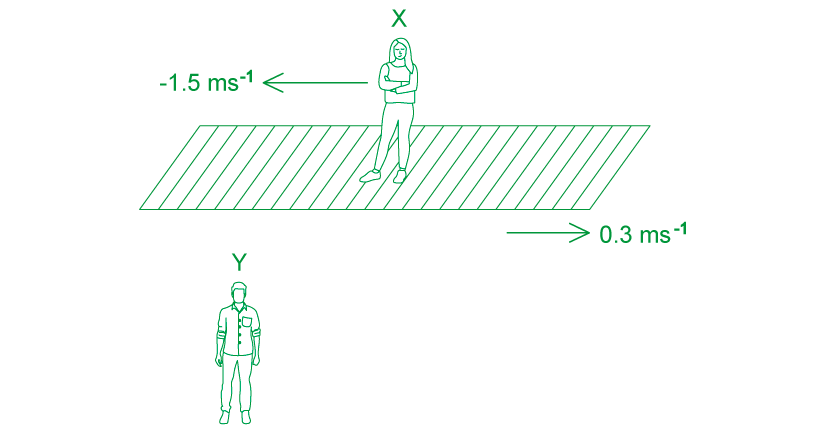
1-5-2-velocity-addition-worked-example-solution-3

Traveller Y (S) measures the velocity of Traveller X (S') to be:

u = u' + (- v)

u =  0.3 – 1.5 = –1.2 m s–1

(c) Assuming Traveller X maintains this motion, determine the velocity of Traveller Y as measured by Traveller X:

List the known quantities:

  • Traveller X is now the stationary observer, S

  • Traveller X sees Traveller Y moving at the same speed as (part (b)) but in the opposite direction (which is the same direction as the travelator - the positive direction)

  • Therefore, Traveller X (S) measures Traveller Y (and therefore reference frame S') to be moving with a velocity

v = 1.2 m s-1

(d) Assuming Traveller X still maintains this motion, Traveller Y now gets up and walks on the ground in the same direction as the motion of the travelator. Traveller Y walks at a velocity of 0.8 m s-1 relative to the ground. Determine the velocity of Traveller Y as measured by Traveller X:

  • Traveller X is still the stationary observer

  • They are making a measurement of an event that is not occurring in their own reference frame

  • They must therefore use vector addition

  • Reference frame S' (the ground) is moving at velocity, v = 1.2 m s-1 as measured by Traveller X

  • Traveller Y is moving with a velocity, u' = 0.8 m s-1 as measured relative to the ground (therefore, as measured from within the moving reference frame, hence, u')

Traveller X (S) measures the velocity of Traveller Y (S') to be:

u = u' + v

u = 0.8 + 1.2 = 2 m s-1

Examiner Tips and Tricks

As you can see, the actual maths is very easy. The hard part is figuring out who is moving, who is stationary, and who is measuring what. When you grasp the rules around that, relativity gets much easier.

Always watch out for the direction of objects in velocity addition, don't just plug in numbers into the equation! The positive direction is determined by the direction of the velocity, v, of the moving reference frame.

It helps to draw a quick sketch of the scenario in your exam and label the velocities.

Worked Example

Two planes are taxiing on the runway on parallel paths. Plane A is heading due north, and Plane B is heading due south. Plane B is travelling at 45 m s-1 and Plane A is travelling at 32 m s-1 relative to an observer on the ground.

Determine the velocity of Plane A relative to Plane B.

Answer:

Identify the observers:

  • 'An observer on the ground' is the stationary observer, S

  • Plane B (doing the measuring) is the moving reference frame, S'

Identify who is measuring whom:

  • Plane A is the object being measured

    • Plane A is being measured by Plane B (S'), therefore, the velocity of Plane A = u'

  • Plane A has a velocity u = 32 m s-1 as measured from a stationary observer (S)

  • Plane B, and therefore reference frame S', has a velocity of 45 m s-1 as measured from a stationary observer

Identify the directions:

  • Setting due north as positive

  • Plane A is travelling due north, u = 32 m s-1

  • Plane B is travelling due south, v = -45 m s-1

Determine the velocity of Plane A as measured from Plane B:

u' = u - v

u' = 32 - (-45)

u' = 77 m s-1

Examiner Tips and Tricks

The language of relativity questions can vary. If A is described as being 'relative' to B, it means that A has that value as measured by B.

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Reference FramesNext:Postulates of Special Relativity
    Ashika

    Author: Ashika

    Expertise: Physics Content Creator

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.