Stoke's Law (DP IB Physics) : Revision Note
Stoke's Law
Viscous Drag
Viscous drag is defined as:
the frictional force between an object and a fluid which opposes the motion between the object and the fluid
This drag force is often from air resistance
Viscous drag is calculated using Stoke’s Law:
Where
Fd = viscous drag force (N)
η = fluid viscosity (N s m−2 or Pa s)
r = radius of the sphere (m)
v = velocity of the sphere through the fluid (ms−1)
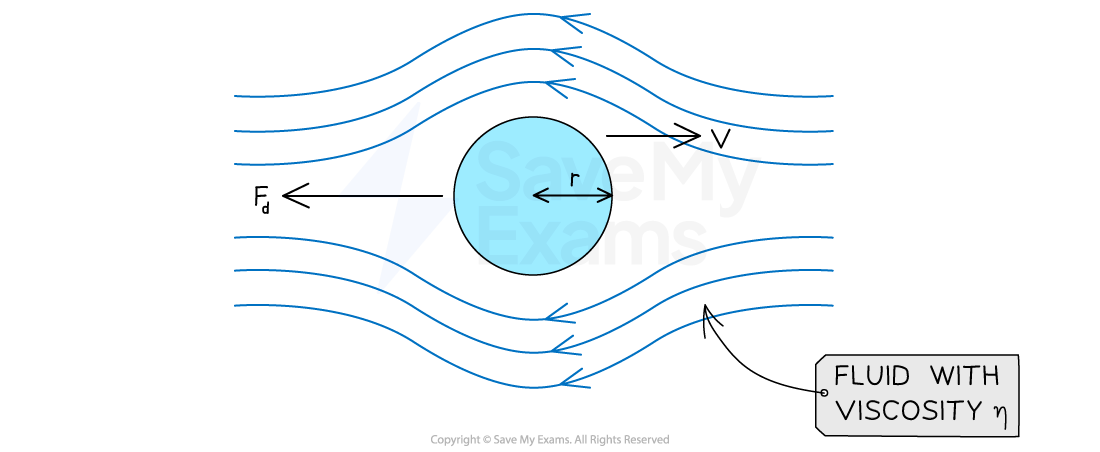
A sphere travelling through air will experience a drag force that depends on its radius, velocity and the viscosity of the liquid
The viscosity of a fluid can be thought of as its thickness, or how much it resists flowing
Fluids with low viscosity are easy to pour, while those with high viscosity are difficult to pour
Water has a lower viscosity than ketchup as it is easier to pour and flow
The coefficient of viscosity is a property of the fluid (at a given temperature) that indicates how much it will resist flow
The rate of flow of a fluid is inversely proportional to the coefficient of viscosity
The size of the force depends on the:
Speed of the object
Size of the object
Shape of the object
Worked Example
A spherical stone of volume 2.7 × 10–4 m3 falls through the air and experiences a drag force of 3 mN at a particular instant. Air has a viscosity of 1.81 × 10-5 Pa s. Calculate the speed of the stone at that instant.
Answer:
Step 1: List the known quantities
Volume of stone, V = 2.7 × 10–4 m3
Drag force, Fd = 3 mN = 3 × 10–3 N
Viscosity of air, η = 1.81 × 10-5 Pa s
Step 2: Calculate the radius of the sphere, r
The volume of a sphere is
Therefore, the radius, r is:
Step 3: Rearrange the Stoke's law equation for the velocity, v
Step 4: Substitute in the known values

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
