Newton’s Second Law | HL IB Physics Revision Notes 2025

Newton's Second Law

Newton's second law describes the change in motion that arises from a resultant force acting on an object

Newton's second law of motion states:

The resultant force on an object is directly proportional to its acceleration

This can also be written as:

$F = m a$

Where:
- F = resultant force (N)
- m = mass (kg)
- a = acceleration (m s^–2)

This relationship means that objects will accelerate if there is a resultant force acting upon them
The acceleration will always act in the same direction as the resultant force

When unbalanced forces act on an object, the object experiences a resultant force
If the resultant force acts along the direction of the object's motion, the object will:
- Speed up (accelerate)
- Slow down (decelerate)
If the resultant force acts on an object at an angle to its direction of motion, it will:
- Change direction

Resultant Force

Force is a vector quantity with both magnitude and direction
The resultant force is, therefore, the vector sum of all the forces acting on the body
If the object is in motion, then the positive direction is in the direction of motion

Resultant Force horizontal, downloadable AS & A Level Physics revision notes

Resultant forces on a body can be positive or negative depending on their direction

If the resultant force acts at an angle to the direction of motion, the magnitude and direction of the resultant force can be found by
- Combing vectors
- Scale drawings
  - This is covered further in Scale Diagrams

Acceleration

Acceleration is a vector quantity with both magnitude and direction
If the resultant force acts in the direction of an object's motion, the acceleration is positive
If the resultant force opposes the direction of the object's motion, the acceleration is negative
But the acceleration will always act in the same direction as the resultant force

Examiner Tip

It is important to understand that for an object in motion, a resultant force that opposes that motion will cause the object to decelerate, not to suddenly travel backwards.

If no drag forces are present, then the acceleration of a falling object is independent of its mass. This unintuitive fact of physics has been proven by astronauts on the Moon, who simultaneously dropped both a hammer and a feather from equal heights and found that they hit the ground at the same time! (Because there is no air resistance on the Moon.)

Worked example

A rocket produces an upward thrust of 15 MN and has a weight of 8 MN.

(a)

When in flight, the force due to air resistance is 500 kN.

Determine the resultant force on the rocket.

(b)

The mass of the rocket is 0.8 × 10⁵ kg.

Calculate the magnitude and direction of the acceleration of the rocket.

Answer

Part a)

Step 1: Draw a force diagram of the situation

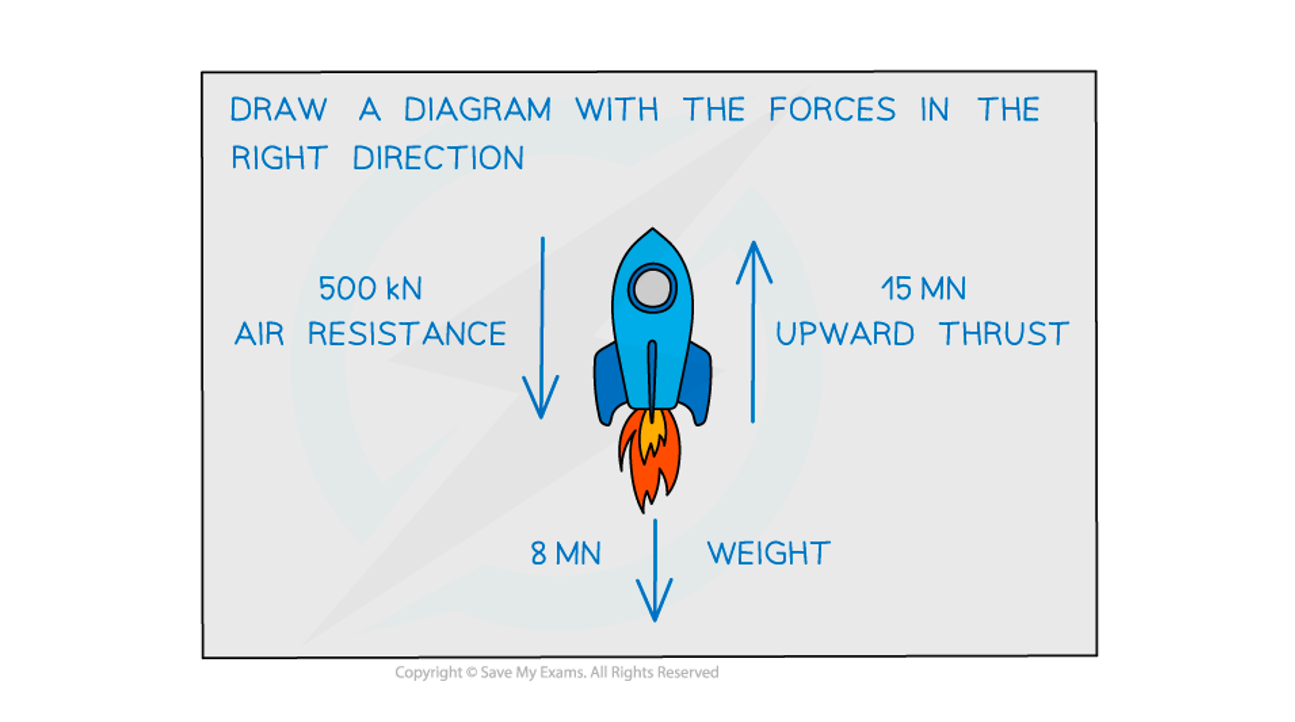
Step 2: Convert the forces into newtons and assign directions

The direction of motion is upwards, therefore upwards is the positive direction
- Air resistance (downward acting) = −500 kN = −500 × 10³ N
- Weight (downward acting) = −8 MN = −8 × 10⁶ N
- Thrust (upward acting) = 15 MN = 15 × 10⁶ N

Step 3: Calculate the resultant force

$F = (15 \times 10^{6}) + (- 8 \times 10^{6}) + (- 500 \times 10^{3})$

$F = 6.5 \times 10^{6} N = 6.5 MN$

The positive value indicates that the resultant force acts in the direction of motion i.e., upwards

Part b)

Step 1: State the equation for Newton's second law and rearrange to make acceleration the subject

$F = m a \Rightarrow a = \frac{F}{m}$

Step 2: Calculate the acceleration and state the direction

$a = \frac{6.5 \times 10^{6}}{0.8 \times 10^{5}}$

$a = 81 m s^{- 2} (2 s . f .)$ upwards

Acceleration is in the same direction as the resultant force

Examiner Tip

Air resistance is a type of fluid resistance because fluids are gases or liquids. The IB specification uses fluid resistance so you should use this term when referring to air resistance in the exam. Air resistance and fluid resistance are drag forces since drag is the force exerted by the particles in a fluid on an object moving it. The symbol for fluid resistance is therefore the same as symbol for drag, F_d.

Worked example

Three forces, 4 N, 8 N, and 24 N act on an object with a mass of 5 kg. Which acceleration is not possible with any combination of these three forces?

A. 1 m s^–²

B. 4 m s^–²

C. 7 m s^–²

D. 10 m s^–^²

Answer:

Step 1: List the values given

Three possible forces at any angle of choice: 4 N, 8 N, and 24 N
Mass of object = 5 kg

Step 2: Consider the relevant equation

Newton's second law relates force and acceleration:

F = m × a

Step 3: Rearrange to make acceleration the focus

$a = \frac{F}{m}$

Step 4: Investigate the minimum possible acceleration

The minimum acceleration would occur when the forces were acting against each other
This is when just the 4 N force is acting on the body
Now check the acceleration:

$a = \frac{4}{5} = 0.8 m s^{- 2}$

Step 4: Investigate the maximum possible acceleration

The maximum acceleration would occur when all three forces are acting in the same direction
This is a total force of

a = 4 + 8 + 24 = 36 N

With acceleration:

$a = \frac{36}{5} = 7.2 m s^{- 2}$

Step 5: Consider this range and the options

Since option D is higher than 7.2 m s^–²; it is not possible that these three forces can produce 10 m s^–²acceleration for this mass
Option D is the correct answer, as it is the only one that is not possible

Examiner Tip

The direction you consider positive is your choice, as long as the signs of the numbers (positive or negative) are consistent throughout the question.

It is a general rule to consider the direction the object is initially travelling in as positive. Therefore all vectors in the direction of motion will be positive and opposing vectors, such as drag forces, will be negative.

Newton's Second Law and Momentum

Newton's second law can also be given in terms of momentum

The resultant force on an object is equal to its rate of change of momentum

This change in momentum is in the same direction as the resultant force

These two definitions are derived from the definition of momentum, as follows:

- Momentum:

$p = m v$

- Rate of change of momentum:

$\frac{∆ p}{∆ t} = m \frac{∆ v}{∆ t}$

- Force:

$F = m \frac{∆ v}{∆ t}$

- Acceleration:

$a = \frac{∆ v}{∆ t}$

- Therefore:

$F = m a$

Worked example

A girl is riding her skateboard down the road and increases her speed from 1 m s^–1 to 4 m s^–¹ in 2.5 s.

The force driving her forward is 72 N.

Calculate the combined mass of the girl and the skateboard. WE - Newtons second law question image, downloadable AS & A Level Physics revision notes

WE - Newtons second law answer image, downloadable AS & A Level Physics revision notes

Newton’s Second Law (HL IB Physics)

Revision Note