Collisions & Explosions in Two-Dimensions (DP IB Physics): Revision Note
Collisions & Explosions in Two-Dimensions
For collisions and explosions occurring in two dimensions, there are components of momentum to consider
Each component of momentum is conserved separately
Since momentum is a vector, it can be resolved into horizontal and vertical components
The sum of the horizontal components will be equal before and after a collision (or explosion)
The sum of the vertical components will be equal before and after a collision (or explosion)
Collisions in two dimensions
Collisions in two dimensions (2D) usually involve an interaction between two objects in a plane
This means the velocity vectors before and after the collision may have both horizontal and vertical components
Consider again the two colliding balls A and B
Before the collision, ball A is moving at speed
and hits stationary ball B
Ball A moves away at speed
and angle
above the horizontal
Ball B moves away at speed
and angle
below the horizontal
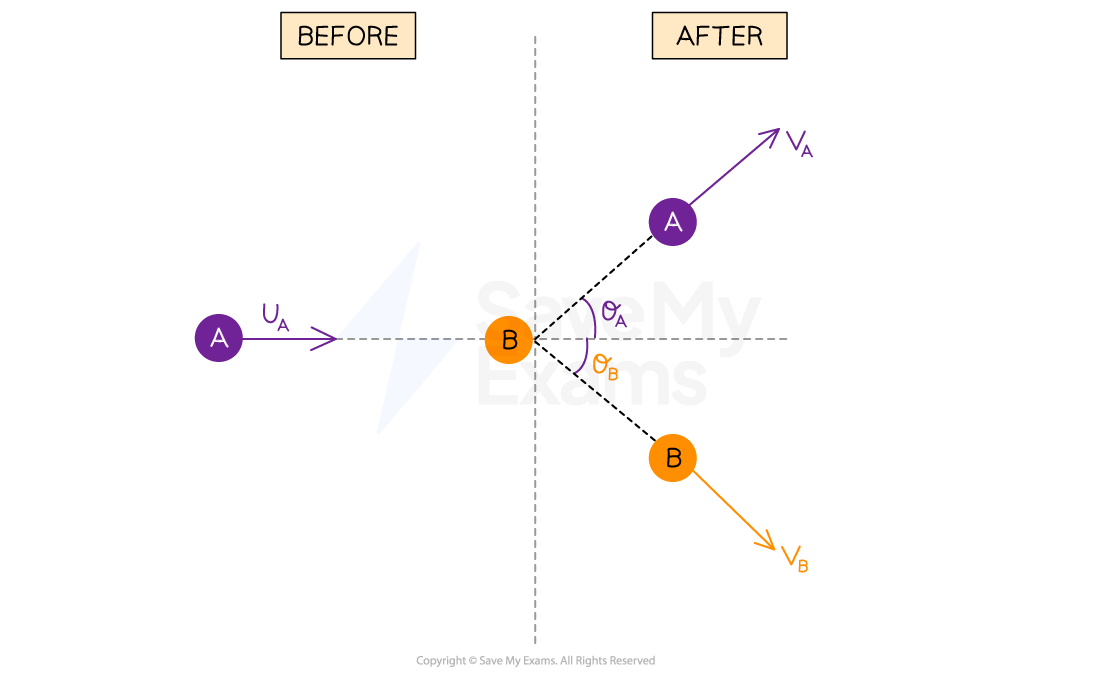
This time, they move off in different directions, so we now need to consider their momentum in the x direction and separately, their momentum in the y direction
This is done by resolving the velocity vector of each ball after the collision
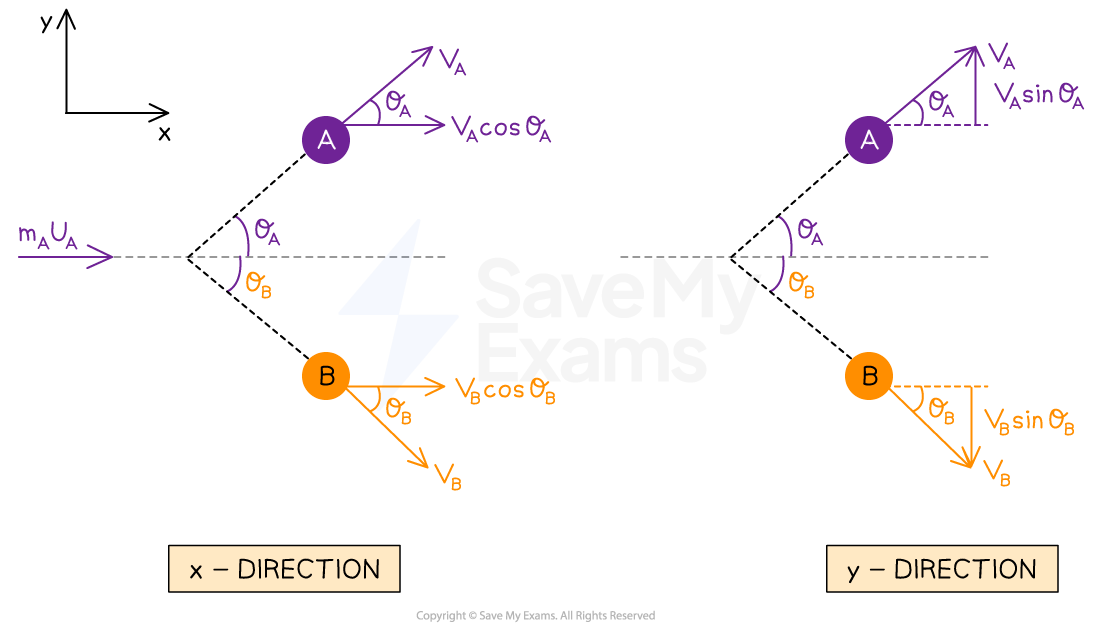
Applying the conservation of momentum along the x direction gives
Applying the conservation of momentum along the y direction gives
The minus sign now comes from B moving downwards, whilst positive y is considered upwards
The momentum before in the y direction is 0 for both balls A and B because B is stationary and A is only travelling in the x direction, so
has no vertical component
Since there are two equations involving sine and cosine, it is helpful to remember the trigonometric identity:
When the collision is elastic, the conservation of linear momentum and energy indicates that
Explosions in two dimensions
Explosions in two dimensions (2D) usually involve one stationary object becoming two or more objects that move away from each other in different directions
Before the explosion, the velocity and, therefore, momentum, are zero
After the explosion, the velocity vectors may have both horizontal and vertical components
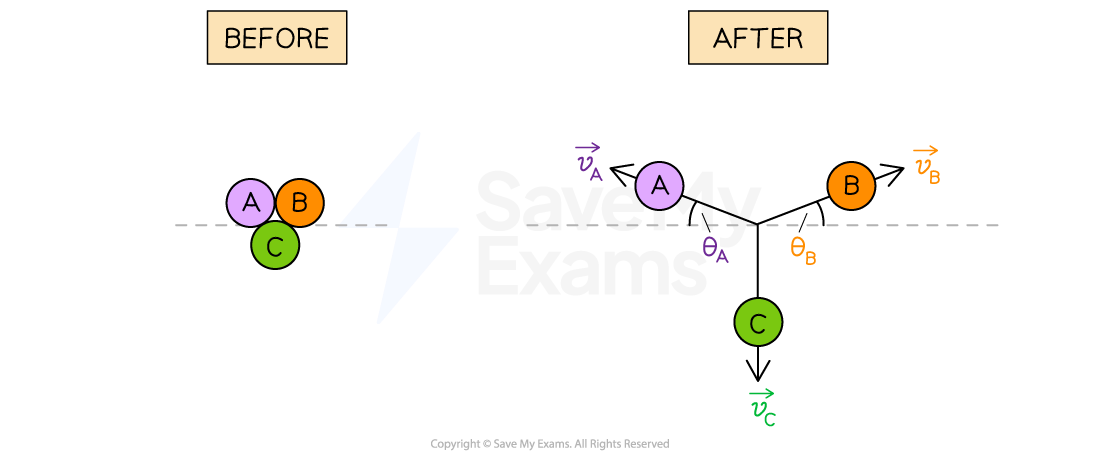
After an explosion of object ABC in two dimensions, three objects, A, B, and C, move off in different directions
Worked Example
A snooker ball of mass 0.15 kg collides with a stationary snooker ball of mass 0.35 kg. After the collision, the second snooker ball moves away with a speed of 0.48 m s–1. The paths of the balls make angles of 43° and 47° with the original direction of the first snooker ball.
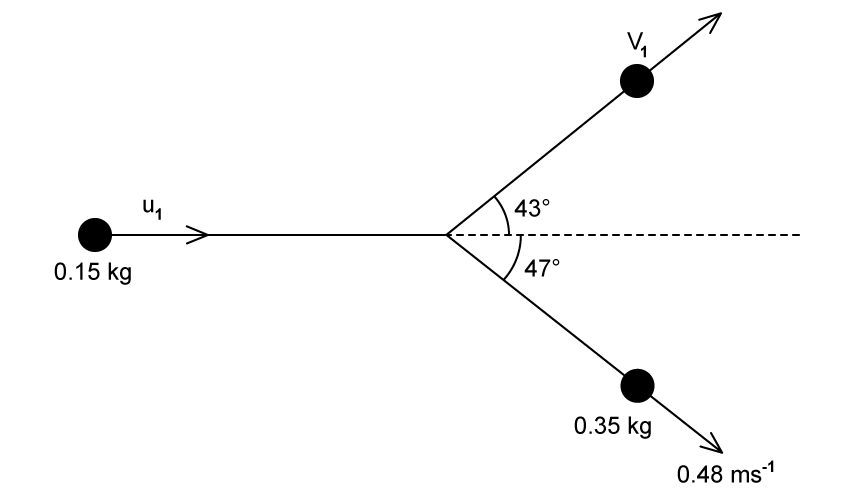
Calculate the initial speed and the final speed
of the first snooker ball.
Answer
Step 1: List the known quantities
Mass of the first snooker ball, m1 = 0.15 kg
Mass of the second snooker ball, m2 = 0.35 kg
Velocity of second ball after, v2 = 0.48 m s–1
Angle of the first ball, θ1 = 43°
Angle of the first ball, θ2 = 47°
Step 2: State an expression for the conservation of momentum in the y (vertical) direction
Step 3: Calculate the speed of the first ball after the collision, v1
Use the conservation of momentum in the y direction to calculate the speed of the first snooker ball after the collision
Step 4: State the equation for the conservation of momentum in the x (horizontal) direction
Step 5: Calculate the speed of the first ball before the collision, u1
Examiner Tips and Tricks
Make sure you clearly label your diagram or write out the known quantities before you substitute values into the question. It's very easy to substitute in the incorrect velocity or mass. Use subscripts such as '1' '2' or 'A' 'B' depending on the question to help keep track of these.
Although you will get full marks either way, it may be easier in these equations to rearrange first and then substitute instead of the other way around, to keep track of the multiple masses and velocities.
Make sure your calculator is in degree mode if your angles are given in degrees!
If you use the fraction function to input your values, remember that you need to close the brackets on the trig functions or it will give you the wrong answer.
Eg.
And if you input the values into your calculator as numerator ÷ denominator, make sure you put brackets around the whole denominator.
Eg.
The trig equation for tanθ is also given on your data sheet under 'Mathematical equations', as well as that for resolving forces.

Unlock more, it's free!
Did this page help you?