The Law of Radioactive Decay (HL) | HL IB Physics Revision Notes 2025

The Law of Radioactive Decay

In radioactive decay, the number of undecayed nuclei falls very rapidly, without ever reaching zero
- Such a model is known as exponential decay
The graph of number of undecayed nuclei against time has a very distinctive shape:

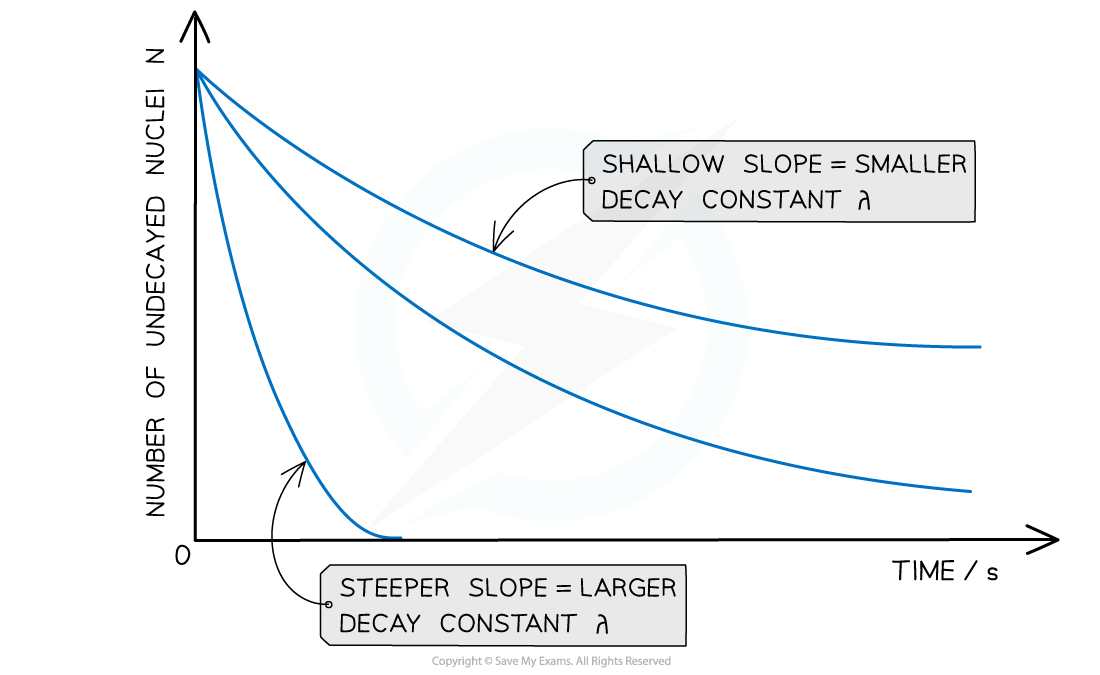
Exponential Decay Graph, downloadable AS & A Level Physics revision notes

Radioactive decay follows an exponential pattern. The graph shows three different isotopes each with a different rate of decay

The key features of this graph are:
- The steeper the slope, the larger the decay constant λ (and vice versa)
- The decay curves always start on the y-axis at the initial number of undecayed nuclei (N₀)

Equations for Radioactive Decay

The number of undecayed nuclei N can be represented in exponential form by the equation:

$N = N_{0} e^{- λ t}$

Where:
- N₀ = the initial number of undecayed nuclei (when t = 0)
- N = number of undecayed nuclei at a certain time t
- λ = decay constant (s^-1)
- t = time interval (s)

The number of nuclei can be substituted for other quantities.
For example, the activity A is directly proportional to N, so it can also be represented in exponential form by the equation:

$A = A_{0} e^{- λ t}$

Where:
- A = activity at a certain time t (Bq)
- A₀ = initial activity (Bq)

The received count rate C is related to the activity of the sample, hence it can also be represented in exponential form by the equation:

$C = C_{0} e^{- λ t}$

Where:
- C = count rate at a certain time t (counts per minute or cpm)
- C₀ = initial count rate (counts per minute or cpm)

Worked example

Strontium-90 decays with the emission of a β-particle to form Yttrium-90. The decay constant of strontium-90 is 0.025 year ^-1.

Determine the activity A of the sample after 5.0 years, expressing the answer as a fraction of the initial activity A₀.

Answer:

Step 1: Write out the known quantities

Decay constant, λ = 0.025 year ^-1
Time interval, t = 5.0 years
Both quantities have the same unit, so there is no need for conversion

Step 2: Write the equation for activity in exponential form

$A = A_{0} e^{- λ t}$

Step 3: Rearrange the equation for the ratio between A and A₀

$\frac{A}{A_{0}} = e^{- λ t}$

Step 4: Calculate the ratio A/A₀

$\frac{A}{A_{0}} = e^{- (0.025 \times 5)} = 0.88$

Therefore, the activity of strontium-90 decreases by a factor of 0.88, or 12%, after 5 years

Worked example

A space probe uses a source containing 4.0 kg of plutonium-238.

Plutonium-238 is an alpha-emitter with a half-life of 87.7 years. Each alpha decay releases 5.5 MeV per emission. The space probe converts this into electrical energy with an efficiency of 32%.

The space probe can continue to operate as long as the power output is maintained at 0.4 kW or above.

Estimate the time, in years, the source is expected to supply power to the space probe.

Answer:

Step 1: List the known quantities

Mass of Pu-238 = 4.0 kg = 4000 g
Molar mass of Pu-238 = 238 g mol⁻¹
Avogadro's constant, $N_{A}$ = 6.02 × 10²³ mol⁻¹
Half-life of Pu-238 = 87.7 years
Energy released per alpha decay = 5.5 MeV
1 electronvolt (eV) = 1.6 × 10⁻¹⁹ J
Efficiency = 32% = 0.32
Final power output, P = 0.4 kW = 400 W

Step 2: Calculate the initial number of nuclei present in the source

238 g of plutonium-238 contains 6.02 × 10²³ atoms (Avogadro's number), so in 4 kg:

Number of nuclei: $N = \frac{m a s s \times N_{A}}{m o l a r m a s s}$

Initial number of nuclei: $N_{0} = \frac{4000 \times (6.02 \times 10^{23})}{238} = 1.012 \times 10^{25}$ nuclei

Step 3: Calculate the initial activity of the source

Decay constant: $λ = \frac{\ln 2}{t_{1 / 2}}$

Activity: $A = λ N$

Combining these gives:

Initial activity: $A_{0} = \frac{N_{0} \ln 2}{t_{1 / 2}}$

$A_{0} = \frac{(1.012 \times 10^{25}) \times \ln 2}{87.7 \times (24 \times 60 \times 60 \times 365)} = 2.54 \times 10^{15}$ Bq

Step 4: Calculate the initial power output of the source

Power output: $P = \frac{∆ E}{∆ t}$

Energy released per decay: $E = (5.5 \times 10^{6}) \times (1.6 \times 10^{- 19}) = 8.8 \times 10^{- 13}$ J

Activity represents the decays per second, so:

Initial power output: $P_{0} = A_{0} E$

$P_{0} = (2.5 \times 10^{15}) \times (8.8 \times 10^{- 13}) = 2200$ W

The electrical power transferred to the probe is:

$P_{0} = 2200 \times 0.32 = 704$ W

Step 5: Use the exponential decay equation to calculate the time of operation

The power available is proportional to the activity of the isotope, so:

Exponential decay of power: $P = P_{0} e^{- λ t}$

$\frac{P}{P_{0}} = e^{- λ t}$

$\ln (\frac{P}{P_{0}}) = - λ t$

$t = - \frac{1}{λ} \ln (\frac{P}{P_{0}}) = - \frac{t_{1 / 2}}{\ln 2} \ln (\frac{P}{P_{0}})$

$t = - \frac{87.7}{\ln 2} \ln (\frac{400}{704}) = 71.5$ years

Therefore, the source is expected to supply power to the space probe for 71.5 years

Examiner Tip

The symbol e is used to represent the exponential constant and is approximately equal to e = 2.718

Make sure you are comfortable using the exponential function on your calculator, it is the button labelled $e^{x}$

The inverse function of $e^{x}$ is the natural logarithmic function, $\ln y$

The rules for exponential functions are the same as the rules for logarithmic functions, so, if $y = e^{x}$ , then $x = \ln y$

The Law of Radioactive Decay (HL) (HL IB Physics)

Revision Note