Magnetic Force between Two Parallel Conductors

A current carrying conductor, such as a wire, produces a magnetic field around it
The direction of the field depends on the direction of the current through the wire
- This is determined by the right hand thumb rule
Parallel current-carrying conductors will therefore either attract or repel each other
- If the currents are in the same direction in both conductors, the magnetic field lines between the conductors cancel out – the conductors will attract each other
- If the currents are in the opposite direction in both conductors, the magnetic field lines between the conductors push each other apart – the conductors will repel each other

20.1 Same or opposite direction current_2

Both wires will attract if their currents are in the same direction and repel if in opposite directions

When the conductors attract, the direction of the magnetic forces will be towards each other
When the conductors repel, the direction of the magnetic forces will be away from each other
The magnitude of each force depends on the amount of current and the length of the wire

The ratio $\frac{F}{L}$ is the force per unit length between two parallel currents I₁ and I₂ separated by a distance r
The force is attractive if the currents are in the same direction and repulsive if they are in opposite directions
It is calculated using the equation:

$\frac{F}{L} = μ_{0} \frac{I_{1} I_{2}}{2 π r}$

T_fIGs2p_4-2-force-eqn-explanation

The forces on each of the current-carrying wires are equal and opposite in direction

The force from wire 2 on wire 1, F₂ = B₂I₁Lsin(θ)
In this situation the magnetic field is perpendicular to the current in the wire, so sin(θ) = 1
F₂ = −F₁ so the force between them is F
The force on a unit length of the wires is then given by $\frac{F}{L} = \frac{B_{2} I_{1} L}{L}$
- Hence, $\frac{F}{L} = B_{2} I_{1}$
The magnitude of the magnetic field at a radial distance, r away from the current conducting wire is: $B = \frac{μ_{0} I}{2 π r}$
- In this case the magnetic field strength from B₂ at a distance r away from wire 2 is: $B_{2} = \frac{μ_{0} I_{2}}{2 π r}$
Substituting for B₂ into the force per unit length equation gives us: $\frac{F}{L} = (\frac{μ_{0} I_{2}}{2 π r}) I_{1}$

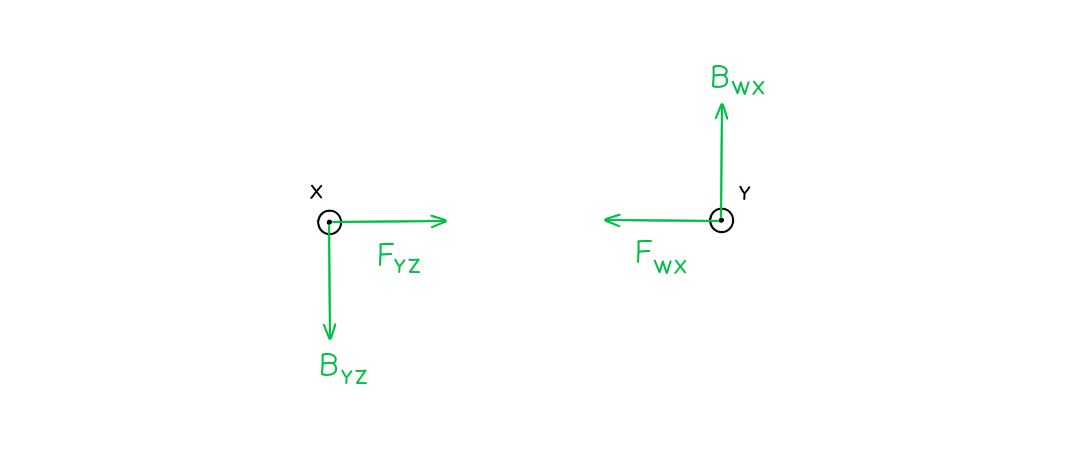
Two long, straight, current-carrying conductors, WX and YZ, are held at a close distance, as shown in diagram 1.

The conductors each carry the same magnitude current in the same direction. A plan view from above the conductors is shown in diagram 2.

On diagram 2, draw arrows, one in each case, to show the direction of:

The magnetic field at X due to the current in wire YZ (label this arrow B_YZ)
The force at X as a result of the magnetic field due to the current in the wire YZ (label this arrow F_YZ)
The magnetic field at Y due to the current in wire WX (label this arrow B_WX)
The force at Y as a result of the magnetic field due to the current in the wire WX (label this arrow F_WX)

Answer:

Newton’s third law: When two bodies interact, the force on one body is equal but opposite in direction to the force on the other body
Therefore, the forces on the wires act in equal but opposite directions

Magnetic Force between Two Parallel Conductors (HL IB Physics)