Magnetic Flux (DP IB Physics): Revision Note
Emf, Magnetic Flux & Magnetic Flux Linkage
Magnetic flux is a quantity which signifies how much of a magnetic field passes perpendicularly through an area
It is defined as:
The product of the magnetic flux density and the cross-sectional area perpendicular to the direction of the magnetic flux density
Magnetic flux when the field and motion are at 90° can be calculated using the simple equation:
Where:
Φ = magnetic flux (Wb)
B = magnetic flux density (T)
A = cross-sectional area (m2)
it is defined by the symbol Φ (greek letter ‘phi’) and measured in units of Webers (Wb)
How does magnetic flux change with angle?
Since the flux is the total magnetic field that passes through a given area
It is a maximum when the magnetic field lines are perpendicular to the plane of the area
It is zero when the magnetic field lines are parallel to the plane of the area
For a coil, the amount of magnetic flux varies as the coil rotates within the field
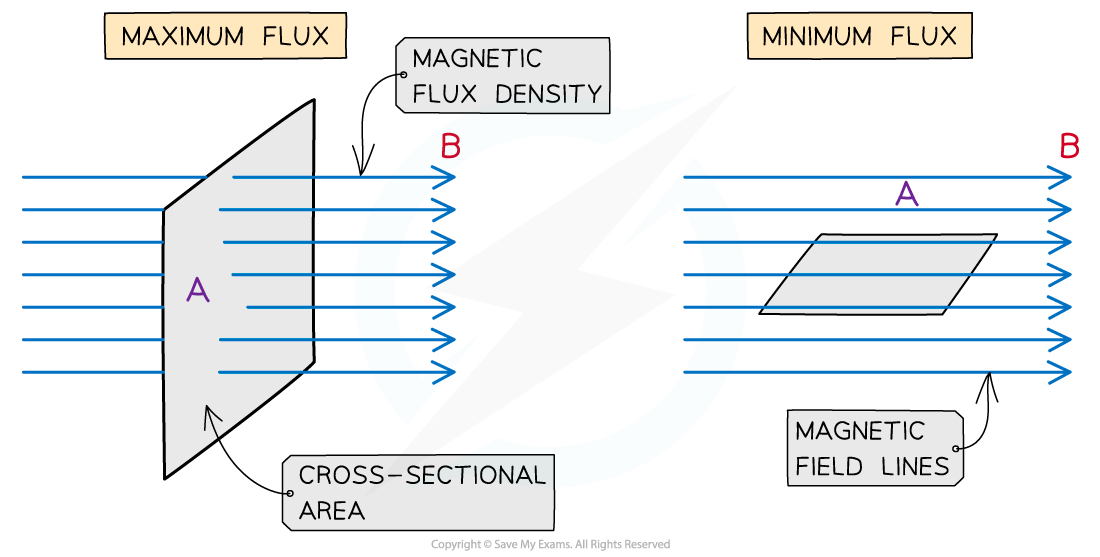
The magnetic flux is maximum when the magnetic field lines and the area they are travelling through are perpendicular
In other words, magnetic flux is the number of magnetic field lines through a given area
When the magnetic field lines are not completely perpendicular to the area A, then the component of magnetic flux density B is perpendicular to the area is taken
The equation then becomes:
Where:
Φ = magnetic flux (Wb)
B = magnetic flux density (T)
A = cross-sectional area (m2)
θ = angle between magnetic field lines and the line perpendicular to the plane of the area (often called the normal line) (degrees)
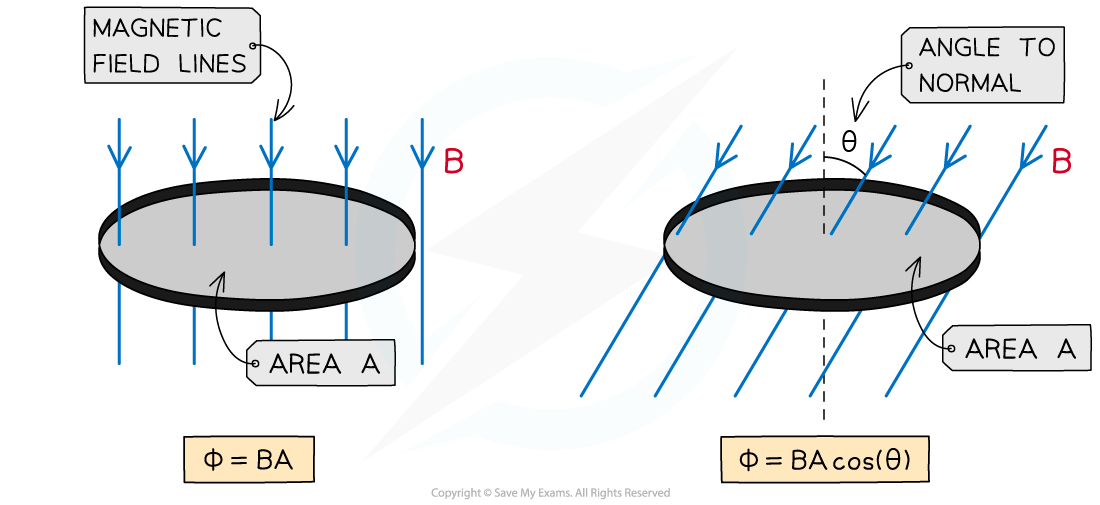
The magnetic flux increases as the angle between the field lines and plane decreases
This means the magnetic flux is:
maximum = BA when cos(θ) =1 therefore θ = 0o. The magnetic field lines are perpendicular to the plane of the area
zero when cos(θ) = 0 therefore θ = 90o. The magnetic field lines are parallel to the plane of the area
Magnetic Flux Linkage
More coils in a wire mean a larger e.m.f. is induced
The magnetic flux linkage is a quantity commonly used for solenoids which are made of N turns of wire
The flux linkage is defined as:
The product of the magnetic flux and the number of turns of the coil
It is calculated using the equation:
Magnetic flux linkage =
Where:
Φ = magnetic flux (Wb)
N = number of turns of the coil
B = magnetic flux density (T)
A = cross-sectional area (m2)
The flux linkage ΦN has the units of Weber turns (Wb turns)
An e.m.f. is induced in a circuit when the magnetic flux linkage changes with respect to time
This means an e.m.f is induced when there is:
A changing magnetic flux density B
A changing cross-sectional area A
A change in angle θ

The magnetic flux through a rectangular coil increases as the angle between the field lines and plane decreases
Magnetic flux linkage also changes with the rotation of the coil
It is at a maximum when the field lines are perpendicular to the plane of the area they are passing through
This is the same pattern as the magnetic flux
Therefore, the component of the flux density which is perpendicular is equal to:
Where:
N = number of turns of the coil
Worked Example
An aluminium window frame has a width of 40 cm and a length of 73 cm.

The frame is hinged along the vertical edge AC. When the window is closed, the frame is normal to the Earth's magnetic field with magnetic flux density 1.8 × 10−5 T.
(a) Calculate the magnetic flux through the window when it is closed.
(b) Sketch the graph of the magnetic flux against the angle between the field lines and the normal when the window is opened and rotated by 180°.
Answer:
(a)
Step 1: Write out the known quantities
Cross-sectional area, A = 40 cm × 73 cm = (40 × 10−2) × (73 × 10−2) = 0.292 m2
Magnetic flux density, B = 1.8 × 10−5 T
Step 2: Write down the equation for magnetic flux
Step 3: Substitute in values
Φ = (1.8 × 10−5) × 0.292 = 5.256 × 10−6 = 5.3 × 10−6 Wb
(b)
The magnetic flux will be at a minimum when the window is opened by 90° and a maximum when fully closed or opened to 180°

Examiner Tips and Tricks
Watch out for area given in cm2 or mm2. For the magnetic flux to be in Webers, the flux density needs to be Tesla and the area in m2.
This area may not always be a square, but a circle as well. The areas of common 2D shapes are given in your data booklet.

Unlock more, it's free!
Did this page help you?