Lenz's Law (HL) (HL IB Physics)

• Lenz’s Law is used to predict the direction of an induced e.m.f in a coil or wire
  • It is a consequence of the principle of conservation of energy

• Lenz's Law is summarised below:

The induced e.m.f is such that it will oppose the change causing it

• Lenz’s law combined with Faraday’s law is given by the equation:  

• This equation shows:
  • When a bar magnet goes through a coil, an e.m.f is induced within the coil due to a change in magnetic flux
  • A current is also induced which means the coil now has its own magnetic field
  • The coil’s magnetic field acts in the opposite direction to the magnetic field of the bar magnet (shown by the minus sign)

• If a direct current (d.c) power supply is replaced with an alternating current (a.c) supply, the e.m.f induced will also be alternating with the same frequency as the supply

Experimental Evidence for Lenz’s Law

• To verify Lenz’s Law, the only apparatus needed is:
  • A bar magnet
  • A coil of wire
  • A sensitive ammeter

• Note: a cell is not required

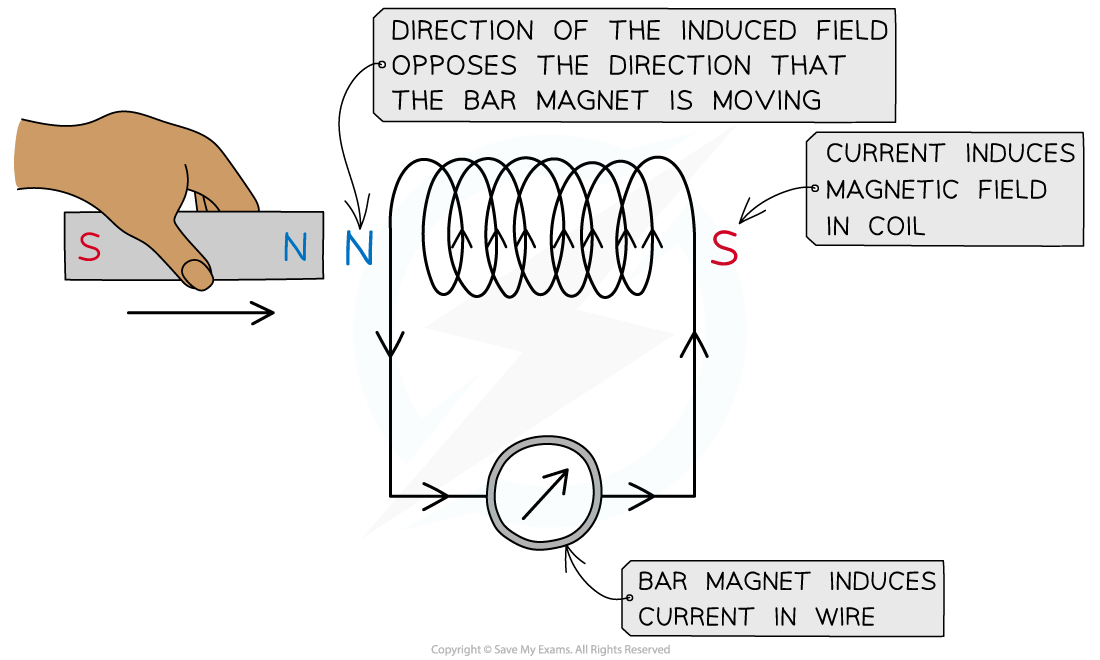
Lenz’s law can be verified using a coil connected in series with a sensitive ammeter and a bar magnet

• A known pole (either north or south) of a bar magnet is pushed into the coil
  • This induces an e.m.f in the coil
  • The induced e.m.f drives a current (because it is a complete circuit)
• Lenz's Law dictates: 
  • The direction of the e.m.f, and hence the current, must be set up to oppose the incoming magnet
  • Since a north pole approaches the coil face, the e.m.f must be set up to create an induced north pole
  • This is because the two north poles will repel each other

• The direction of the current is therefore as shown in the image above
  • The direction of the current can be verified using the right-hand grip rule
  • Fingers curl around the coil in the direction of current and the thumb points along the direction of the flux lines, from north to south 
  • Therefore, the current flows in an anti-clockwise direction in the image shown, in order to induce a north pole opposing the incoming magnet

• Reversing the magnet direction would give an opposite deflection on the voltmeter
  • Lenz's Law would then predict a south pole induced at the coil entrance (next to the bar magnet)
  • This would create a north pole at the exist, attracting the bar's south pole attempting to leave 
  • Therefore, the induced e.m.f always produces effects to oppose the changes causing it
• This means:
  • The coil will try and push the bar magnet to stop it from entering 
  • The coil will try and pull the bar magnet to stop it from leaving
  • This means the poles of the coil swaps around as the bar magnet travels through

• Lenz's Law is a direct consequence of the principle of conservation of energy
  • Electromagnetic effects will not create electrical energy out of nothing
  • In order to induce and sustain an e.m.f, for instance, work must be done in order to overcome the repulsive effect due to Lenz's Law

• When changes in current within a circuit occur, particularly when the current is alternating at high frequencies, changes in magnetic flux will also occur
• Two types of induction can be observed
  • Self-induction - induction within the same circuit
  • Mutual induction - induction between circuits

• These both occur as a consequence of Lenz's law

Self Induction

• When induction occurs within the same circuit, this is known as self-induction
• Self-induction is defined as

The effect in which a change in the current tends to produce an induced emf which opposes the change of current in the same circuit

• The induced current is produced by a back e.m.f. i.e. an induced e.m.f. that opposes a change of current (in the same circuit)
  • Note: this is the same induced e.m.f. as described by Lenz's law

Self-induction occurs within the same circuit. The primary magnetic field induces a current which opposes the primary current.

• The back e.m.f. is proportional to minus the rate of current change

back e.m.f. 

Mutual Induction

• When induction occurs in a separate circuit from the one producing the change, this is known as mutual induction
• Mutual induction is defined as

The effect in which a change in the current in one circuit tends to produce an induced emf which opposes the change of current in a neighbouring circuit

• An important application of mutual induction is transformers

Transformers

• A transformer is

A device that changes high alternating voltage at low current to low alternating voltage at high current, and vice versa

• A transformer is designed to reduce heat energy loss whilst transmitting electricity through power lines from power stations to the national grid
• A transformer is made up of:
  • A primary coil
  • A secondary coil
  • An iron core

Components of a transformer

• The primary and secondary coils are wound around the soft iron core
  • The soft iron core is necessary because it enhances the strength of the magnetic field from the primary to the secondary coil
  • Soft iron is used because it can easily be magnetised and demagnetised

A step-up transformer has more turns in the secondary coil than primary

• In the primary coil, an alternating current producing an alternating voltage is applied
  • This creates an alternating magnetic field inside the iron core and therefore a changing magnetic flux linkage

• A changing magnetic field passes through to the secondary coil through the iron core
  • This results in a changing magnetic flux linkage in the secondary coil and from Faraday's Law, an e.m.f is induced

• An e.m.f produces an alternating output voltage from the secondary coil
  • The output alternating voltage is at the same frequency as the input voltage

• In a step-up transformer
  • The secondary coil has more turns than the primary coil
  • Hence, the secondary voltage is larger than the primary voltage

• In a step-down transformer
  • The primary coil has more turns than the secondary coil
  • Hence, the primary voltage is larger than the secondary voltage