Orbital Motion, Speed & Energy (HL) | HL IB Physics Revision Notes 2025

Orbital Motion, Speed & Energy

Since most planets and satellites have near-circular orbits, the gravitational force F_G between two bodies (e.g. planet & star, planet & satellite) provides the centripetal force needed to stay in an orbit
- Both the gravitational force and centripetal force are perpendicular to the direction of travel of the planet

Consider a satellite with mass m orbiting Earth with mass M at a distance r from the centre travelling with linear speed v

$F_{G} = F_{c i r c}$

Equating the gravitational force to the centripetal force for a planet or satellite in orbit gives:

$\frac{G M m}{r^{2}} = \frac{m v^{2}}{r}$

The mass of the satellite m will cancel out on both sides to give:

$v^{2} = \frac{G M}{r} \Rightarrow v_{o r b i t a l} = \sqrt{\frac{G M}{r}}$

Where:
- $v_{o r b i t a l}$ = orbital speed of the smaller mass (m s⁻¹)
- G = Newton's Gravitational Constant
- M = mass of the larger mass being orbited (kg)
- r = orbital radius (m)

This means that all satellites, whatever their mass, will travel at the same speed v in a particular orbit radius r
- Since the direction of a planet orbiting in circular motion is constantly changing, the centripetal acceleration acts towards the planet

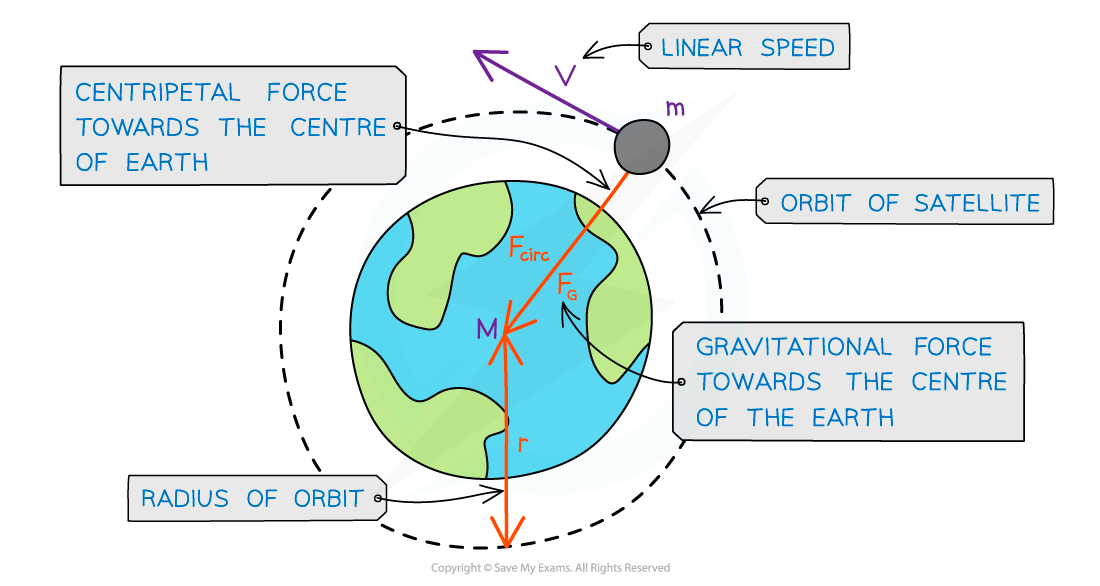
Circular motion satellite, downloadable AS & A Level Physics revision notes

A satellite in orbit around the Earth travels in circular motion

Energy of an Orbiting Satellite

An orbiting satellite follows a circular path around a planet
Just like an object moving in circular motion, it has both kinetic energy (E_k) and gravitational potential energy (E_p) and its total energy is always constant
An orbiting satellite's total energy is calculated by:

Total energy = Kinetic energy + Gravitational potential energy

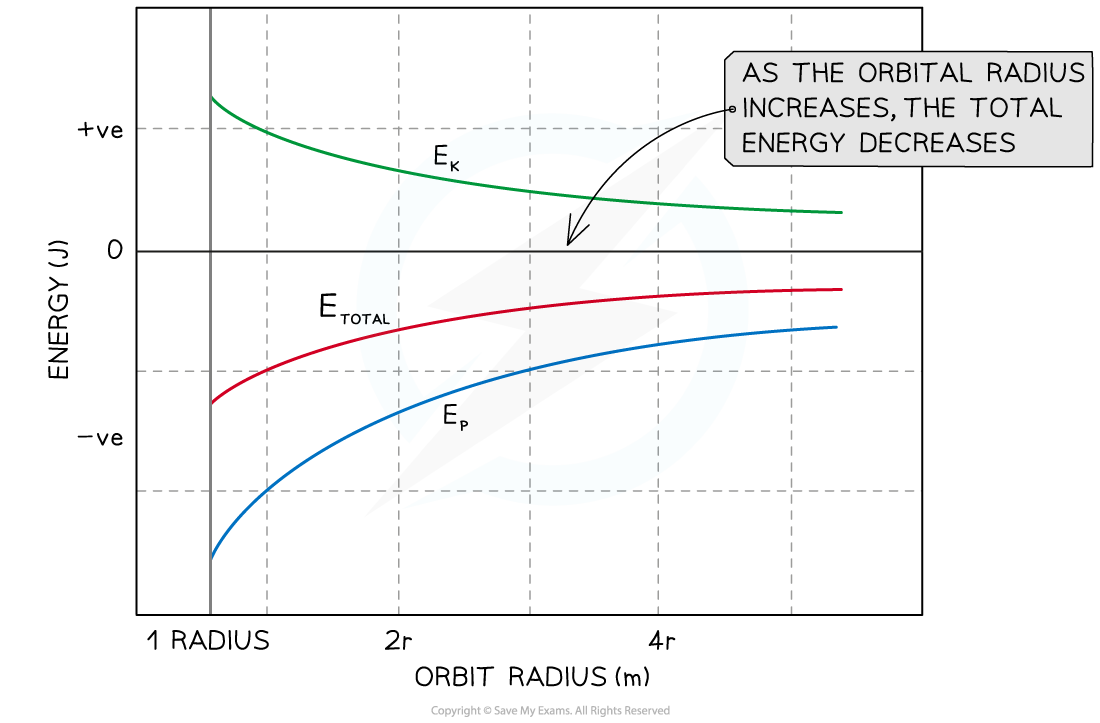
10-2-6-energy-diagram-ib-hl

A graph showing the kinetic, potential and total energy for a mass at varying orbital distances from a massive body

This means that the satellite's E_k and E_p are also both constant in a particular orbit
- If the orbital radius of a satellite decreases its E_kincreases and its E_pdecreases
- If the orbital radius of a satellite increases its E_kdecreases and its E_pincreases

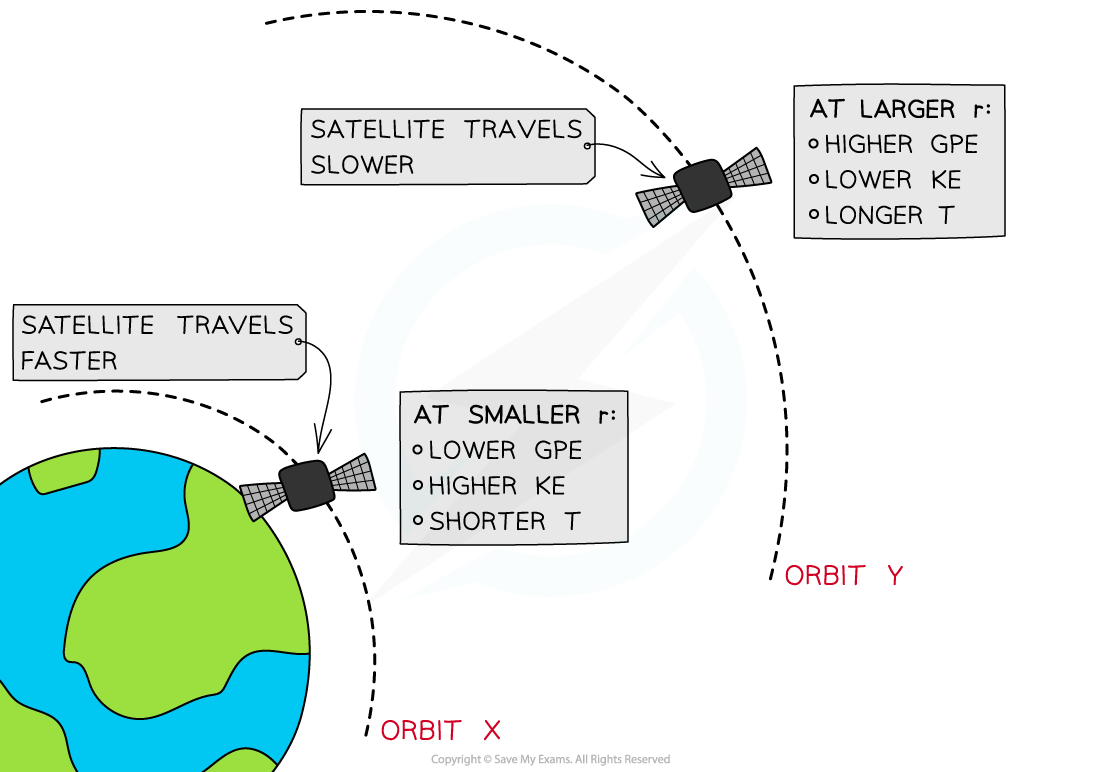
Energy of Orbiting Satellite, downloadable AS & A Level Physics revision notes

At orbit Y, the satellite has greater GPE and less KE than at at orbit X

A satellite is placed in two orbits, X and Y, around Earth
At orbit X, where the radius of orbit r is smaller, the satellite has a:
- Larger gravitational force on it
- Higher speed
- Higher E_k
- Lower E_p
- Shorter orbital time period, T
At orbit Y, where the radius of orbit r is larger, the satellite has a:
- Smaller gravitational force on it
- Smaller speed
- Lower E_k
- Higher E_p
- Longer orbital time period, T

Worked example

A binary star system constant of two stars orbiting about a fixed point B.

The star of mass M₁ has a circular orbit of radius R₁ and mass M₂ has a radius of R₂. Both have linear speed v and an angular speed ⍵ about B.

Worked example - circular orbits in g fields, downloadable AS & A Level Physics revision notes

In terms of G, M₂, R₁ and R₂, write an expression for

(a)

the angular speed ⍵ of mass M₁

(b)

the time period T of each star

Answer:

(a) Angular speed:

The centripetal force on mass M₁ is:

$F = \frac{M_{1} {v_{1}}^{2}}{R_{1}} = \frac{M_{1} {(ω R_{1})}^{2}}{R_{1}} = M_{1} R_{1} ω^{2}$

The gravitational force between the two masses is:

$F = \frac{G M_{1} M_{2}}{{(R_{1} + R_{2})}^{2}}$

Equating these expressions gives:

$M_{1} R_{1} ω^{2} = \frac{G M_{1} M_{2}}{{(R_{1} + R_{2})}^{2}}$

Rearrange for angular velocity

$ω = \sqrt{\frac{G M_{2}}{R_{1} {(R_{1} + R_{2})}^{2}}}$

(b) Orbital period:

The relation between angular speed and orbital period is

$ω = \frac{2 π}{T} \Rightarrow T = \frac{2 π}{ω}$

Using the expression for angular velocity from part (a)

$T = 2 π \div \sqrt{\frac{G M_{2}}{R_{1} {(R_{1} + R_{2})}^{2}}} = 2 π \sqrt{\frac{R_{1} {(R_{1} + R_{2})}^{2}}{G M_{2}}}$

Worked example

Two identical satellites, X and Y, orbit a planet at radii R and 3R respectively.

Which one of the following statements is incorrect?

A. Satellite X has more kinetic energy and less potential energy than satellite Y

B. Satellite X has a shorter orbital period and travels faster than satellite Y

C. Satellite Y has less kinetic energy and more potential energy than satellite X

D. Satellite Y has a longer orbital period and travels faster than satellite X

Answer: D

Satellite Y is at a larger orbital radius, therefore it will have a longer orbital period, since $T^{2} \propto R^{3}$
Being at a larger orbital radius means the gravitational force will be weaker for Y than for X
So, satellite Y will travel much slower than X as centripetal force: $F \propto v^{2}$
Travelling at a slower speed means satellite Y will have less kinetic energy, as $E_{K} \propto v^{2}$ , and, therefore, more potential energy than X

Satellite X

Satellite Y

orbital radius

orbital period

orbital speed

kinetic energy

potential energy

smaller

shorter

faster

greater

lower

larger

longer

slower

lower

greater

Therefore, all statements are correct except in D where it says 'Satellite Y travels faster than satellite X'

Examiner Tip

If you can't remember which way around the kinetic and potential energy increases and decreases, think about the velocity of a satellite at different orbits.

When it is orbiting close to a planet, it experiences a larger gravitational pull and therefore orbits faster. Since the kinetic energy is proportional to v², it, therefore, has higher kinetic energy closer to the planet. To keep the total energy constant, the potential energy must decrease too.

Orbital Motion, Speed & Energy (HL) (HL IB Physics)

Revision Note